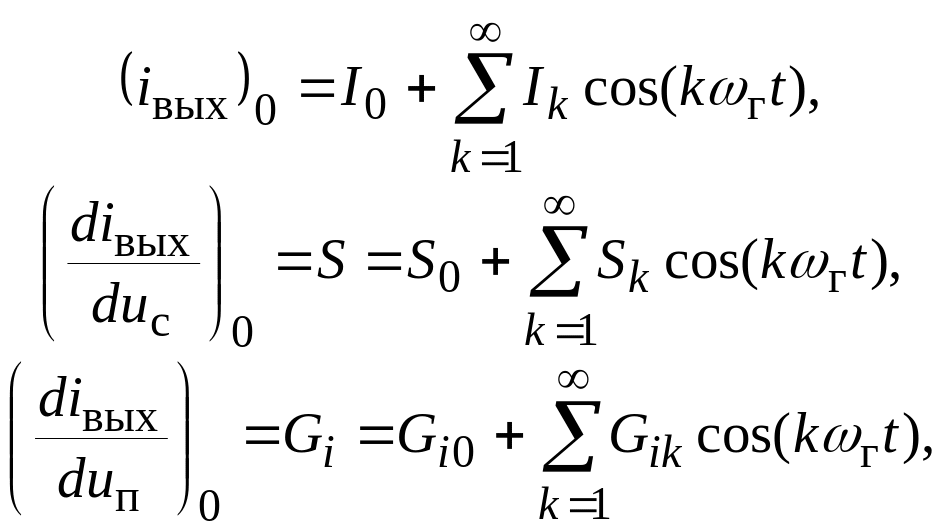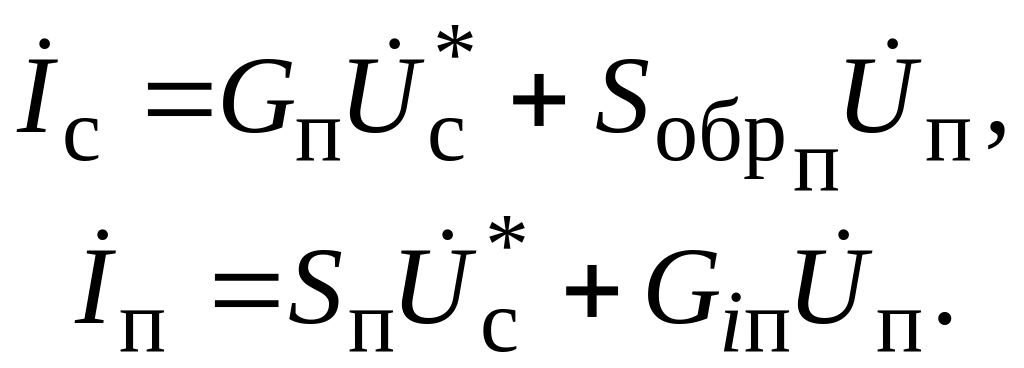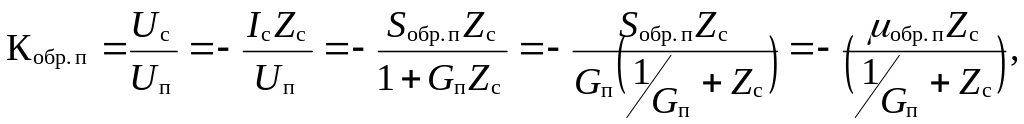131

VII. Преобразователи частоты

В преобразователе частоты происходит изменение несущей частоты колебания сигнала. По отношению к колебаниям гетеродина нелинейность преобразовательного элемента должна проявлять себя возможно сильнее. В подавляющем большинстве случаев выполняется условие, что . Роль нелинейных или параметрических элементов в современных преобразователях частоты обычно выполняют транзисторы – биполярные или полевые, а также диоды – вакуумные и полупроводниковые.

В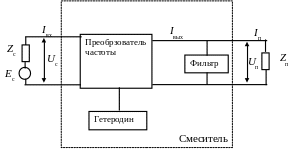 общем случае преобразователи частоты включают в себя преобразующий элемент (смеситель), гетеродин, фильтр, выделяющий колебания промежуточной частоты (рис.7.1).

Рис.7.1. Структурная схема преобразователя частоты

В основу классификации преобразователей частоты обычно кладут тип преобразовательного элемента и особенности схемотехники.

Так различают преобразователи частоты

- транзисторные,

-диодные,

-перемножительные,

по схемотехнике

- однотактные,

- двухтактные (балансные),

- кольцевые.

1.1. Основные качественные показатели преобразователей

частоты

1. Коэффициент преобразования

или ,

где E_с -эдс источника сигнала.

2. Входное сопротивление , или входная проводимость .

3. Выходное сопротивление , или выходная проводимость .

7.2 Общая теория преобразователей частоты

Считаем, что преобразовательный элемент является безынерционным. Тогда входной и выходной токи в каждый момент времени определяются мгновенными значениями u_с, u_п, u_г согласно данной системе уравнений:

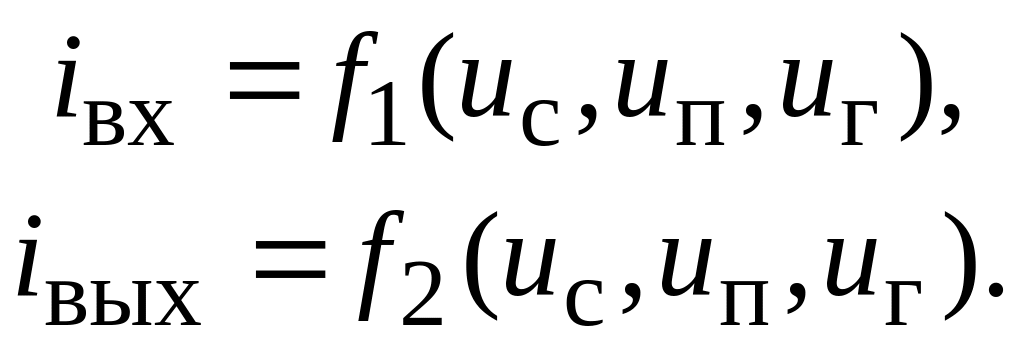
(7.1)

Учитывая, что обычно выполняется условие u_с, u_п << u_г, выражение для выходного тока можно представить в виде разложения в ряд Тейлора в точке, задаваемой мгновенными значениями напряжения сигнала, и сигнала на промежуточной частоте (ввиду малости напряжений сигнала и сигнала на промежуточной частоте можно ограничиться лишь первыми членами разложения):

.

(7.2)

По своему смыслу есть некоторая проводимость, которая может быть названа обобщенной крутизной преобразующего элемента, а функция – его обобщенной выходной проводимостью.

Индекс "0" указывает, что соответствующие функции даны для рабочей точке, задаваемой совместным действием напряжения гетеродина и постоянных напряжений. Обычно напряжение гетеродина является гармоническим колебанием . Поэтому функции являются периодическими функциями относительно частоты гетеродина и могут быть разложены в ряд Фурье.

Выбрав начало отсчета так, чтобы соответствующие функции разложения были четными, можно записать:

(7.3)

где I₀, S₀, G_i0 – постоянные составляющие выходного тока, крутизны и выходной проводимости; I_k, S_k, G_ik – амплитуды k-х гармоник указанных величин.

Сигнал на выходе преобразовательного элемента может быть представлен в следующем виде:

(7.4)

Примем в качестве промежуточной частоты комбинационную частоту .

Выделим из спектра выходного колебания составляющую сигнала и соответствующую ей составляющую на промежуточной частоте , где f_с, f_п – начальные фазы, отсчитываемые относительно фазы напряжения гетеродина, принятой за нулевую. Тогда выходной ток можно представить в следующем виде:

.

(7.5)

Учитывая, что произведение косинусов может быть преобразовано по формуле , получим окончательное выражение для выходного тока преобразователя частоты:

.

(7.6)

Таким образом, мгновенное значение тока промежуточной частоты образуется векторным сложением двух слагаемых, первое из которых обусловлено собственно процессом преобразования, а второе – реакцией цепи нагрузки.

Выражение (1.6) в комплексном виде может быть представлено в следующем виде:

,

(7.7)

где – комплексно-сопряженная амплитуда сигнала.

Аналогично можно получить выражение для входного тока преобразовательного элемента. Выражение для тока сигнала на входе преобразовательного элемента представляется следующим образом:

(7.8)

где G_{обр k} – амплитуда k-й гармоники обобщенной проводимости обратной связи преобразовательного элемента, – комплексно-сопряженная амплитуда напряжения промежуточной частоты; G₀ – постоянная составляющая обобщенной входной проводимости преобразовательного элемента.

Система указанных уравнений полностью описывает поведение преобразователя частоты, как линейного 4-полюсника

(7.9)

Таким образом, свойства преобразователя описываются в системе Y-параметров. Соответственно можно определить и Y-параметры для преобразователя частоты:

– крутизна преобразования; – входная проводимость преобразователя; – внутренняя проводимость преобразователя; – крутизна обратного преобразования.

(71.10)

С учетом предыдущих замечаний система уравнений, описывающих поведение преобразователя частоты, может быть представлена в виде

(7.11)

Из системы уравнений (7.11) можно получить коэффициенты преобразования и обратного преобразования , а также определить входную и выходную проводимости преобразователя при реальной нагрузке Z_н и внутреннем сопротивлении источника сигнала.

Из второго уравнения системы (7.11), учитывая, что , получаем:

(7.12)

Откуда путем последовательных преобразований находим

или

(7.13)

где – внутренний коэффициент передачи преобразователя, – его внутреннее сопротивление.

Таким образом, как следует из системы уравнений (7.11), преобразователь можно представить эквивалентными схемами, которые аналогичны эквивалентным схемам усилителей радиосигналов (рис.7.2.), но с заменой m на _п, R на R_iп, S на S_п.

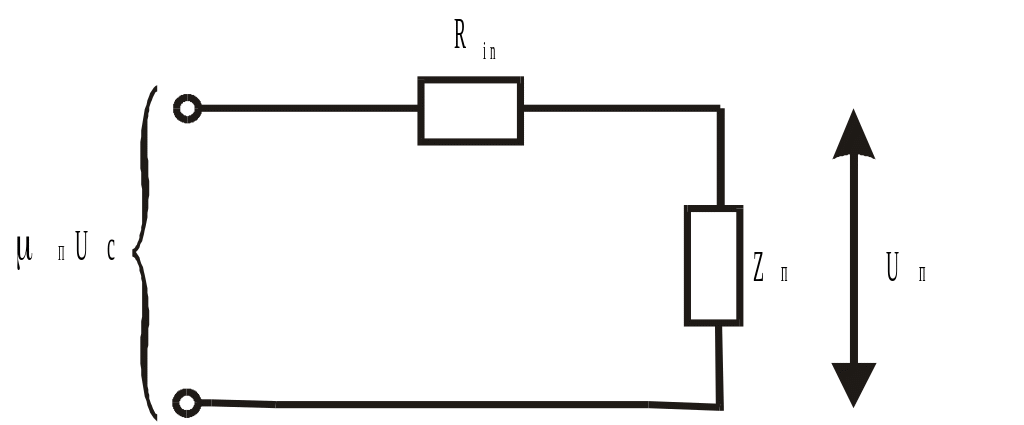
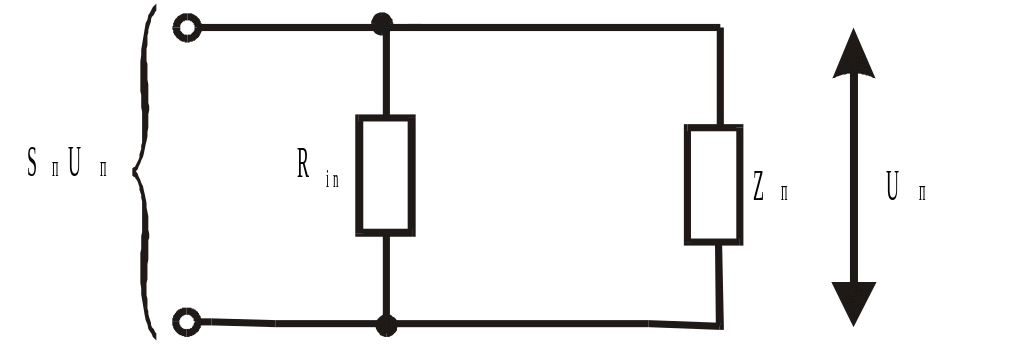
Рис.7.2. Эквивалентные схемы усилителей радиосигналов

Коэффициент передачи преобразователя можно определить из второго уравнения системы (7.11). Для этого заменяем и делаем простые преобразования:

(7.14)

или

(7.15)

Из выражения (7.15) легко получается выражение для коэффициента передачи преобразователя в следующем виде:

(7.16)

Коэффициент обратного преобразования легко найти из первого уравнения системы (7.11) с учетом того, что (при рассмотрении обратного преобразования полагаем что и поэтому

(7.17)

Отсюда имеем:

или

(7.18)

Далее коэффициент обратного преобразования определяется следующим образом:

(7.19)

где _{обр. п} – внутренний обратный коэффициент передачи.

Входная проводимость преобразователя может быть получена из первого уравнения системы (7.11). Для этого разделим обе части уравнения на U_с и после несложных преобразований получим:

(7.20)

Из второго уравнения системы (7.11) путем деления обоих частей уравнения на U_п найдем выражение для выходной проводимости преобразователя:

(7.21)

Таким образом, определены все основные показатели преобразователя частоты.