26. Вихревое электрическое поле.

Неподвижный контур находится в переменном магнитном поле.

Сила Лоренца на неподвижные заряды не действует.

Для объяснения явления электромагнитной индукции необходимо считать, что переменное магнитное поле вызывает появление электрического поля – вихревого электрического поля, под действием которого и возникает индукционный ток в замкнутом проводнике.

Переменное магнитное поле возбуждает в пространстве вихревое электрическое поле независимо от наличия проводящего контура. Замкнутый контур лишь позволяет обнаружить по возникновению в нем индукционного тока существование этого электрического поля (гипотеза Максвелла).

Уравнение Максвелла:

Циркуляция вектора напряженности E_Bi индуцированного электрического поля по неподвижному проводящему контуру L равна э.д.с.

электромагнитной индукции εi .

По определению ЭДС индукции:

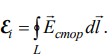
Напряженность результирующего поля: Е  Е_кул  Е_стор  Е_стор  Е  Е_кул, где Е_кул – напряженность электростатического поля, Е_стор – напряженность поля сторонних сил.

так как электростатическое поле – потенциальное.

В последнем уравнении берѐтся частная производная по времени /t, так как рассматривается только возникновение э.д.с. индукции εi вследствие зависимости магнитной индукции от времени (т.е. имеем неподвижный контур).

следовательно, электрическое поле, возбуждаемое переменным магнитным полем, – вихревое.

Отличие вихревого электрического поля от электростатического:

1. Силовые линии вихревого электрического поля – замкнуты.

2. Работа по перемещению единичного положительного точечного заряда в вихревом электрическом поле (циркуляция вектора Е) не равна нулю, а равна э.д.с. индукции εi.

27. Ток смещения.

Ток смещения или абсорбционный ток — величина, которая прямо пропорциональна скорости изменения электрической индукции.

Токи смещения можно наблюдать только тогда, когда электрическое смещение D переменно, то есть наблюдают его колебания. Объемную плотность тока в этом случае можно измерить и рассчитать по формуле:

Вывод данного физического содержания теории Максвелла о токах смещения позволяет утверждать, что переменные электрические поля являются источниками переменных магнитных полей. Следует отметить, что для определения плотности тока смещения используют производную вектора D.

Вектор электрической индукции измеряется по формуле:

Где ε₀ — электрическая постоянная, E — вектор напряженности, P — вектор поляризации.

Уравнение для тока смещения будет иметь следующий вид:

Токи поляризации являются следствием движения связанных заряженных частиц, которые не обладают принципиальными отличиями по сравнению со свободными зарядами. Основываясь на данном факте, можно объяснить порождение магнитного поля токами поляризации. Принципиальной новизной отличается вторая часть уравнения тока смещения:

Данная формула не обладает связью с перемещением заряженных частиц, но также формирует магнитное поле. Можно сделать вывод, что в вакуумной среде любое изменение электрического поля по времени является причиной образования магнитного поля.

Нужно обратить внимание на то, что определение тока смещения для диэлектриков имеет какое-то обоснование, так как в них действительно можно наблюдать смещение зарядов в атомах и молекулах. Но этот термин применяют и к вакууму, в котором отсутствуют заряды, а, следовательно, и их смещение.

Мгновенное значение силы тока I = dq/dt. Плотность тока проводимости в непосредственной близости от поверхности обкладок определяется выражением:

где S – площадь обкладки, q – распределенный на ней заряд,  – поверхностная плотность заряда.

Видим, что сила тока в проводе

, т.е., она однозначно связана с быстротой изменения

электрического смещения электрического поля.

Отсюда следует, что меняющееся поле конденсатора вызывает так же магнитное поле, как ток, имеющий силу

Эта величина получила название плотности тока смещения. Пользуясь этим понятием, можно выразить второе положение Максвелла в следующем: переменное во времени электрическое поле вызывает такое же магнитное поле, как и ток проводимости с плотностью j_ñì, определяемой формулой (300).

В общем случае электрическое поле может быть неоднородным и может зависеть не только от времени, но и от координат. В этом случае выражение для плотности тока смещения будет:

где знак частной производной указывает на то, что магнитное поле зависит от быстроты изменения электрического смещения во времени в каждой точке поля.