18. Дифракция на круглом отверстии и экране.
В соответствии с методом зон Френеля плоский фронт можно разбить на кольцевые зоны Френеля. Границы зон Френеля представляют собой окружности. Радиус k-й зоны Френеля равен ρk = √ kbλ.
Число зон Френеля, укладывающихся в круглом отверстии, определяем по радиусу: k = R2 / bλ.
Если число зон в отверстии четное, то в точке Р наблюдается темное пятно (волны от соседних зон приходят в точку Р в противофазе и попарно компенсируют друг друга).
При нечетном числе зон результирующая амплитуда колебаний А = (А1 / 2) + (А2n+1 / 2).
При небольших отверстиях амплитуды А1 и А2n+1 мало отличаются друг от друга, поэтому результирующая амплитуда А = (А1 / 2) + (А2n+1 / 2) = А1, в точке P наблюдается светлое пятно.
Если отверстие в непрозрачном экране оставляет открытой только одну зону Френеля, то амплитуда колебаний в точке Р возрастает в два раза. Если открыть две зоны, то амплитуда колебаний обращается в нуль. Если изготовить непрозрачный экран, который оставлял бы открытыми только несколько нечетных (четных) зон, то амплитуда колебаний будет резко возрастет. Такие пластинки, обладающие свойством фокусировать свет, называются зонными пластинками.
При дифракции света на круглом диске радиусом R закрытыми оказываются зоны Френеля первых номеров от 1 до k. При этом амплитуда колебаний в точке наблюдения А = Аk+1 / 2.
Если диск закрывает зоны не с большим номером, то в центре картины при дифракции света на диске наблюдается интерференционный максимум.
Согласно симметрии интерференционная картина на экране вокруг центрального светлого (или темного) пятна должна иметь вид чередующихся светлых и темных колец с центром в точке Р.
19. Дифракция Фраунгофера на одной щели.
Дифракцию, наблюдаемую в параллельных лучах, называют дифракцией Фраунгофера.
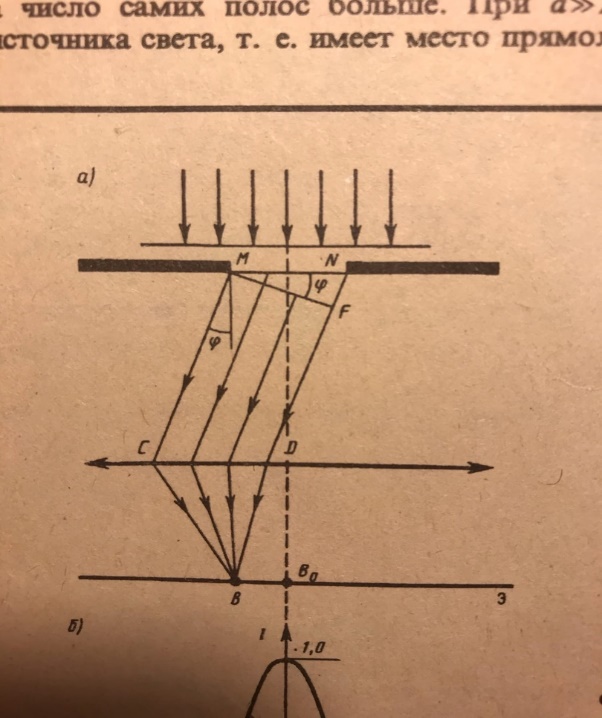
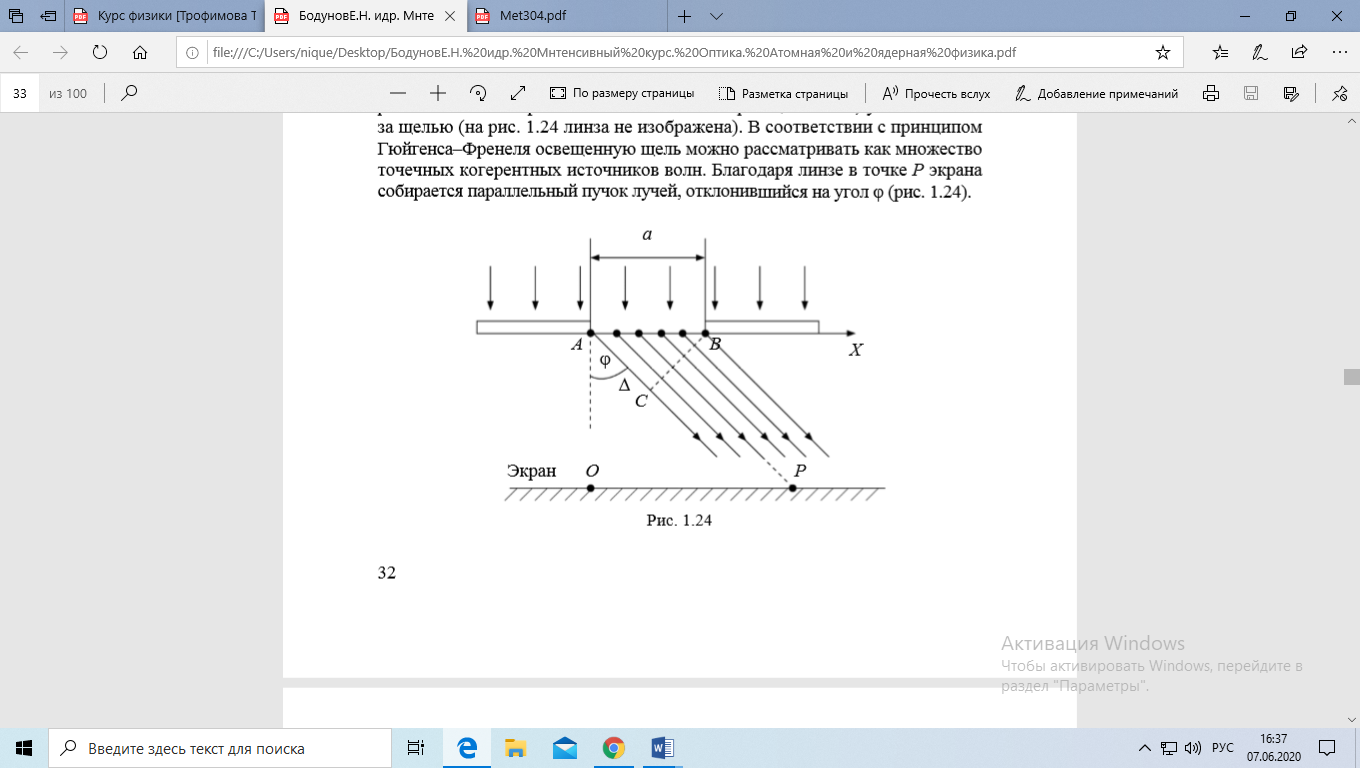
Благодаря линзе в точке Р экрана собирается параллельный пучок лучей, отклонившийся на угол φ, от которого зависит число зон Френеля.
Разность хода Δ крайних лучей из пучка Δ = a*sin φ, где а – ширина щели.
Если при наблюдении из точки Р в щели помещается четное число зон Френеля, то их вклады взаимно погасятся и в точке Р будет наблюдаться минимум интенсивности света.
Уравнение a*sin φkmin = kλ, k = 1, 2, 3 … является условием дифракционных минимумов, в котором угол φkmin направлен на минимум с номером k.
Если число зон Френеля четное, то условие дифракционных максимумов a*sin φkmах = (k + ½) * λ/2, k = 1, 2, 3 …
В направлении φ = 0 щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т. е. в центре наблюдается центральный дифракционный максимум.
20. Дифракционная решетка. Формула дифракционной решетки. Применение дифракционной решетки.
Явление дифракции используется для спектрального анализа и точного измерения длин волн. Для этой цели применяются дифракционные решетки.
Дифракционная решетка – это оптический прибор, представляющий собой поверхность, на которую нанесено большое число равноотстоящих друг от друга щелей. Работает по принципу дифракции света – явления отклонения света от прямолинейного распространения при встрече с препятствием.
Дифракционная решетка на просвет представляют собой периодические структуры, выгравированные делительной машиной на поверхности стеклянной пластинки, а дифракционная решетка на отражение – на поверхности металлической пластинки.
Простейшая дифракционная решетка состоит из N одинаковых щелей шириной b, отделенных друг от друга непрозрачными промежутками шириной а. Величина d = a+b называется периодом решетки.
Если на дифракционную решетку перпендикулярно ее поверхности падает пучок параллельных световых лучей, то в соответствии с принципом Гюйгенса–Френеля каждая щель представляет собой совокупность вторичных источников когерентных волн, способных интерферировать друг с другом.
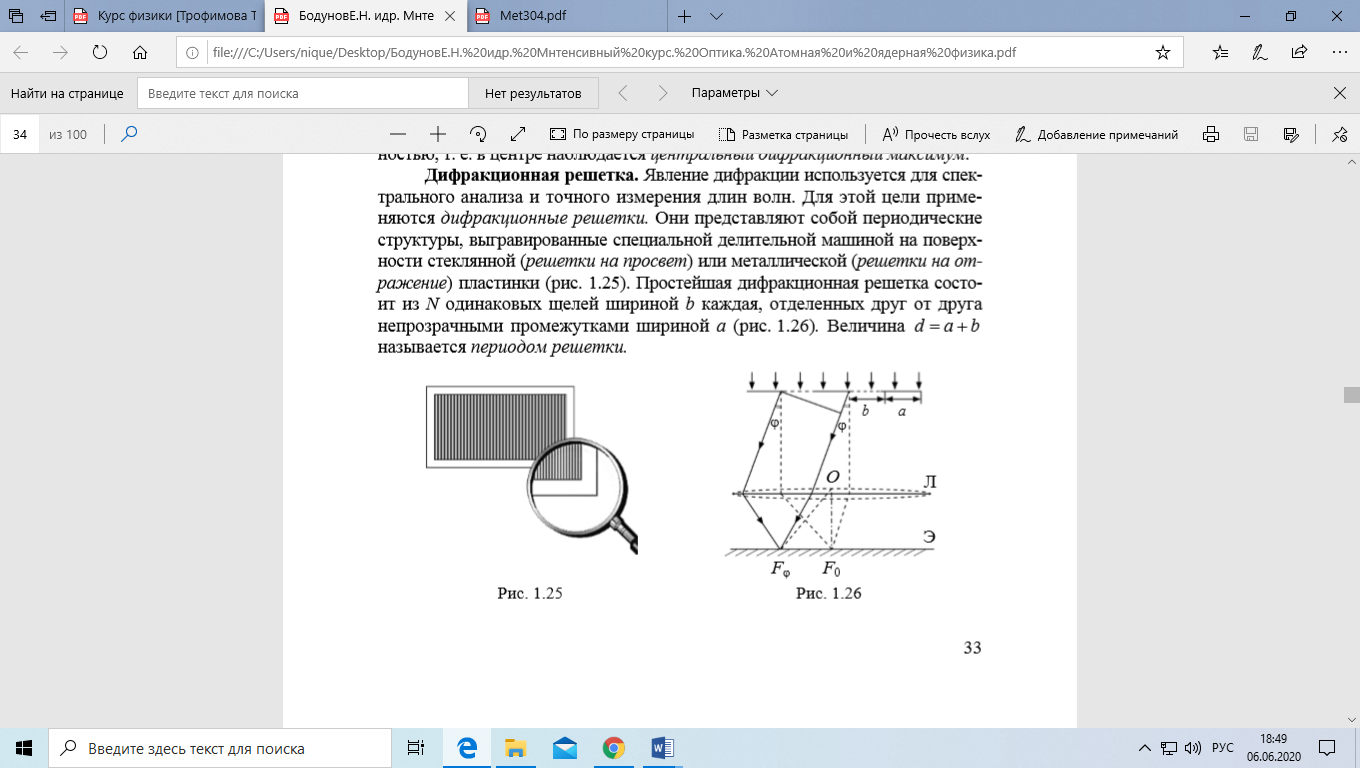
Для того чтобы в точке Fφ наблюдался интерференционный максимум, разность хода Δ между волнами, исходящими из соседних щелей, должна быть равна целому числу длин волн: Δ = d*sinφ = kλ, k = 0, ±1, ±2, … (формула дифракционной решетки), где d – период дифракционной решетки, φ – угол наблюдения максимума, k – порядок дифракционного максимума, λ – длина волны.