13. Интерференция света. Когерентность источников света.
Интерференцией световых волн называется явление наложения световых волн, при котором происходит их устойчивое во времени взаимное усиление в одних точках пространства и ослабление в других. Результат интерференции световых волн можно наблюдать на экране в виде чередующихся светлых и темных мест, совокупность которых называется интерференционной картиной.
Необходимым условием интерференции волн является их когерентность, т.е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Колебания и их источники называются когерентными, если разность их фаз не зависит от времени (является постоянной). Когерентными могут быть колебания (и источники) только одинаковой частоты.
Условию когерентности удовлетворяют монохроматические волны – неограниченные в пространстве волны одной строго постоянной частоты. Ни один реальный источник не дает строго монохроматического света, поэтому волны, излучаемые независимыми источниками, всегда некогерентные, и на опыте интерференция света от этих источников не наблюдается.
Когерентные волны можно получить, если излучение одного источника разделить на два пучка, заставить каждый пучок пройти разные оптические пути, а затем наложить их друг на друга. Практически это можно осуществить с помощью экранов и щелей.
14. Интерференционная картина от двух когерентных источников световых волн.
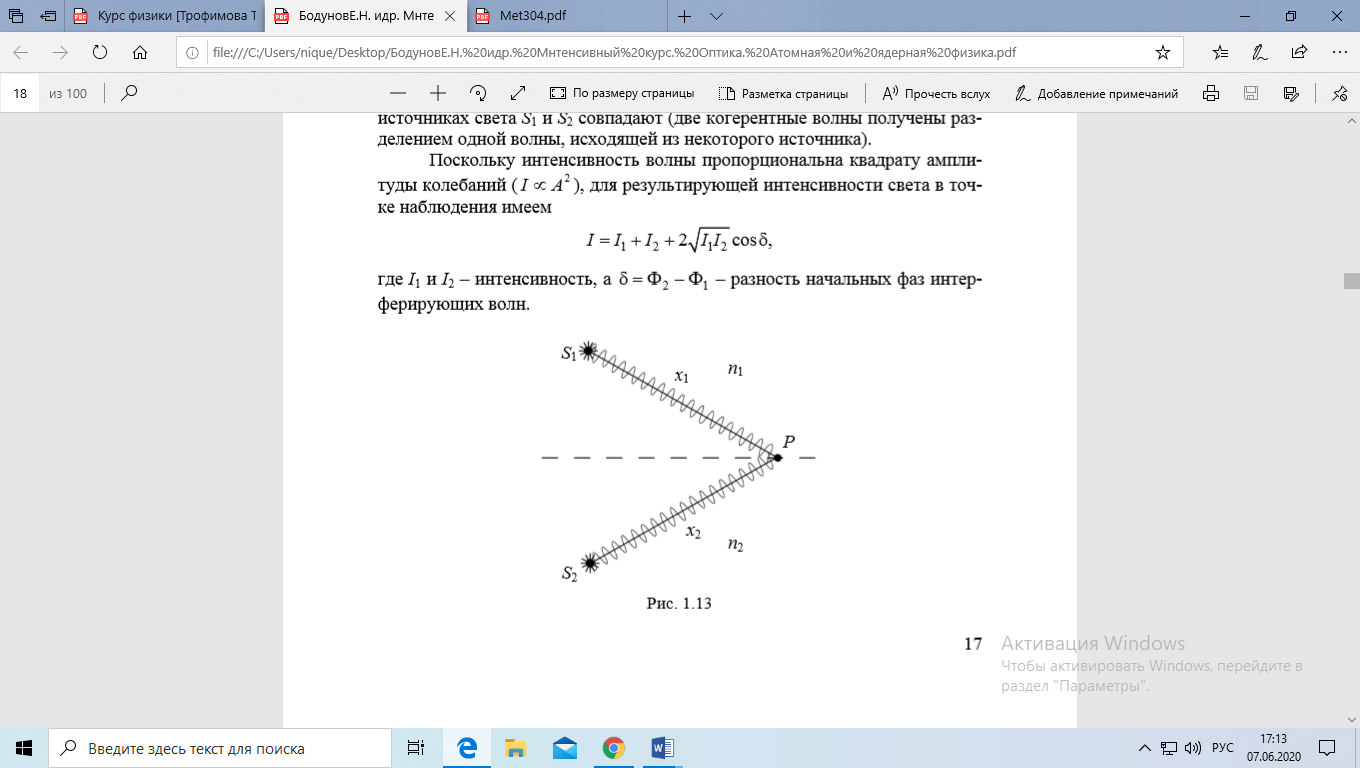
Рассмотрим две бесконечные монохроматические световые волны, пришедшие в точку наблюдения Р от источников света S1 и S2. Расстояния от источников света до точки Р равны x1 и x2. В этой точке колебания векторов напряженности электрического поля равной частоты Е = А*cos(ωt+Ф) складываются.
Пусть направления колебаний векторов Е1 и Е2 совпадают. Тогда амплитуда результирующего колебания А = √ (А12 + А22 + 2А1А2*cos (Ф2 – Ф1)), где A1 и A2 – амплитуды, а Ф2 и Ф1 – начальные фазы колебаний в точке Р, зависящие от расстояний x1 и x2.
Далее предполагаем, что φ1 = φ2, т. е. начальные фазы колебаний в источниках света S1 и S2 совпадают. Результирующая интенсивности света в точке наблюдения равна I = I1 + I2 + 2√(I1I2) *cos δ, где I1 и I2 – интенсивность, а δ = Ф2 – Ф1 – разность начальных фаз интерферирующих волн.
В точках пространства Р, в которых cos δ > 0 , результирующая интенсивность света больше суммы интенсивностей двух волн ( I > I1 + I2), а в точках, где cos δ < 0 , суммарная интенсивность I < I1 + I2 . Таким образом, при наложении двух когерентных световых волн происходит пространственное перераспределение светового потока: в одних местах экрана возникают максимумы, а в других – минимумы интенсивности, т. е. наблюдается интерференция света. Выражение 2√(I1I2) *cos δ называется интерференционным членом.
Если интерференционный член везде равен нулю, то наблюдается только взаимное усиление света (I = I1 + I2), а интерференция отсутствует. Если две волны возбуждают в точке пространства колебания разного направления, т.е. векторы Е1 и Е2 не параллельны друг другу, то интерференционный член содержит скалярное произведение этих векторов: Е1Е2 = E1E2cosα, где α – угол между векторами.
При наложении двух световых волн одинаковой частоты, колебания которых происходят во взаимно перпендикулярных плоскостях (α = π/2), интерференционный член обращается в нуль (скалярное произведение Е1Е2 = 0), и интерференция отсутствует (I = I1 + I2).
Разность фаз и разность хода. Разность фаз двух волн, пришедших в точку Р, будет зависеть только от пути, который прошла каждая волна, и показателя преломления среды. Путь, который прошла волна от источника до точки Р, называется геометрическим ходом волны.
Оптическая длина пути равна произведению показателя преломления среды на геометрический ход волны. Оптическая разность хода двух волн Δ = │ n1x1 – n2x2│.
Начальная разность фаз колебаний в точке наблюдения интерференции P связана с оптической разностью хода соотношением δ = 2πΔ / λ0, где λ0 – длина волны в вакууме. Таким образом, результат интерференции двух волн определяется величиной ∆ (оптической разностью хода волн).
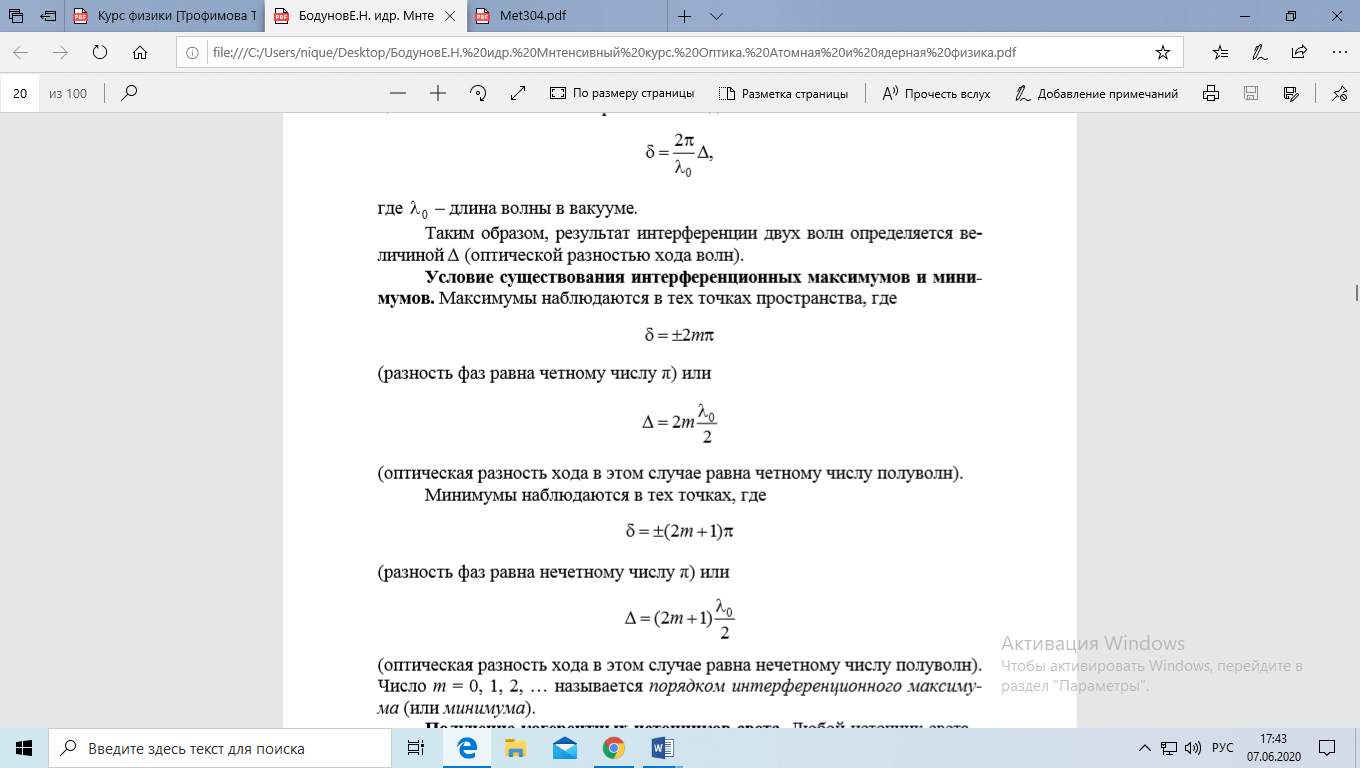
Условие существования интерференционных максимумов и минимумов. Максимумы наблюдаются в тех точках пространства, где
Опыт Юнга. Источник света - ярко освещенная щель S. Световая волна, исходящая из источника S, падает на две узкие равноудаленные щели S1 и S2. Щели S1 и S2 играют роль когерентных источников. Интерференционная картина наблюдается на экране Э, расположенном на некотором расстоянии параллельно щелям S1 и S2. Расположение максимумов и минимумов интерференции на экране определяется оптической разностью хода Δ = L2 – L1.
