25. Фотоны. Энергия и импульс фотона.

Свет представляет собой поток корпускул – фотонов, или квантов света, распространяющихся в вакууме со скоростью света и обладающих энергией Е = hν (Дж).

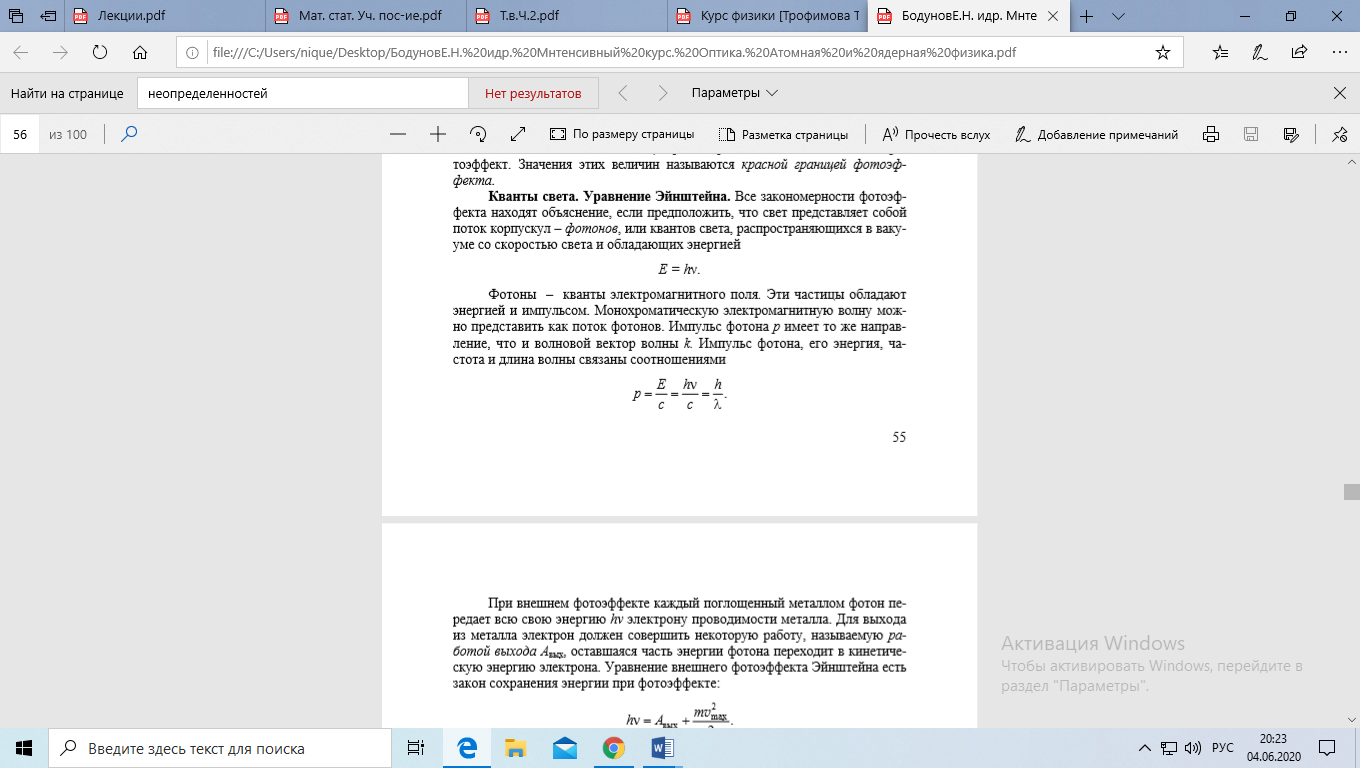
Фотоны – кванты электромагнитного поля. Эти частицы обладают энергией и импульсом. Монохроматическую электромагнитную волну можно представить, как поток фотонов. Импульс фотона, его энергия, частота и длина волны связаны соотношениями

Масса фотона находится из закона взаимосвязи массы и энергии m = hν/c². Фотон – элементарная частица, которая всегда движется со скоростью с — скоростью распространения света в вакууме, и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы электрона, протона и нейтрона, которые обладают отличной от нуля массой покоя.

Фотон, как и любая другая частица характеризуется энергией, массой и импульсом. Представленные выше выражения связывают корпускулярные характеристики фотона – массу, импульс и энергию – с волновой характеристикой света – частотой.

Так как фотоны обладают импульсом, то свет, падающий на тело, должен оказывать на него давление. Согласно квантовой теории, давление света на поверхность обусловлено тем, что каждый фотон при соударении с поверхностью передает ей свой импульс.

Давление света объясняется и на основе волновой теории света. Электромагнитная волна – совокупность периодически меняющейся в пространстве и во времени напряженности электрического E и магнитного Н полей. При взаимодействии с поверхностью вещества эти поля оказывают силовое воздействие на электроны атомов вещества. Электрическое поле заставляет электроны двигаться со скоростью v, противоположной по направлению вектору E. На движущиеся электроны со стороны магнитного поля волны действует сила Лоренца, которая по правилу левой руки перпендикулярна v (т. е. Е) и Н и направлена вдоль распространения волны. Эта сила и есть сила светового давления.

26. Эффект Комптона.

Эффектом Комптона называется упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и γ-излучения) на свободных электронах вещества, сопровождающееся увеличением длины волны этого излучения.

Эффект Комптона объясняется на основе квантовых представлений о природе света: излучение имеет корпускулярную природу, т.е. представляет собой поток фотонов, эффект Комптона есть результат упругого столкновения фотонов со свободными электронами вещества. В процессе этого столкновения фотон передает электрону часть своих энергии и импульса в согласии с законами сохранения.

Электрон отдачи – электрон, на котором происходит рассеяние.

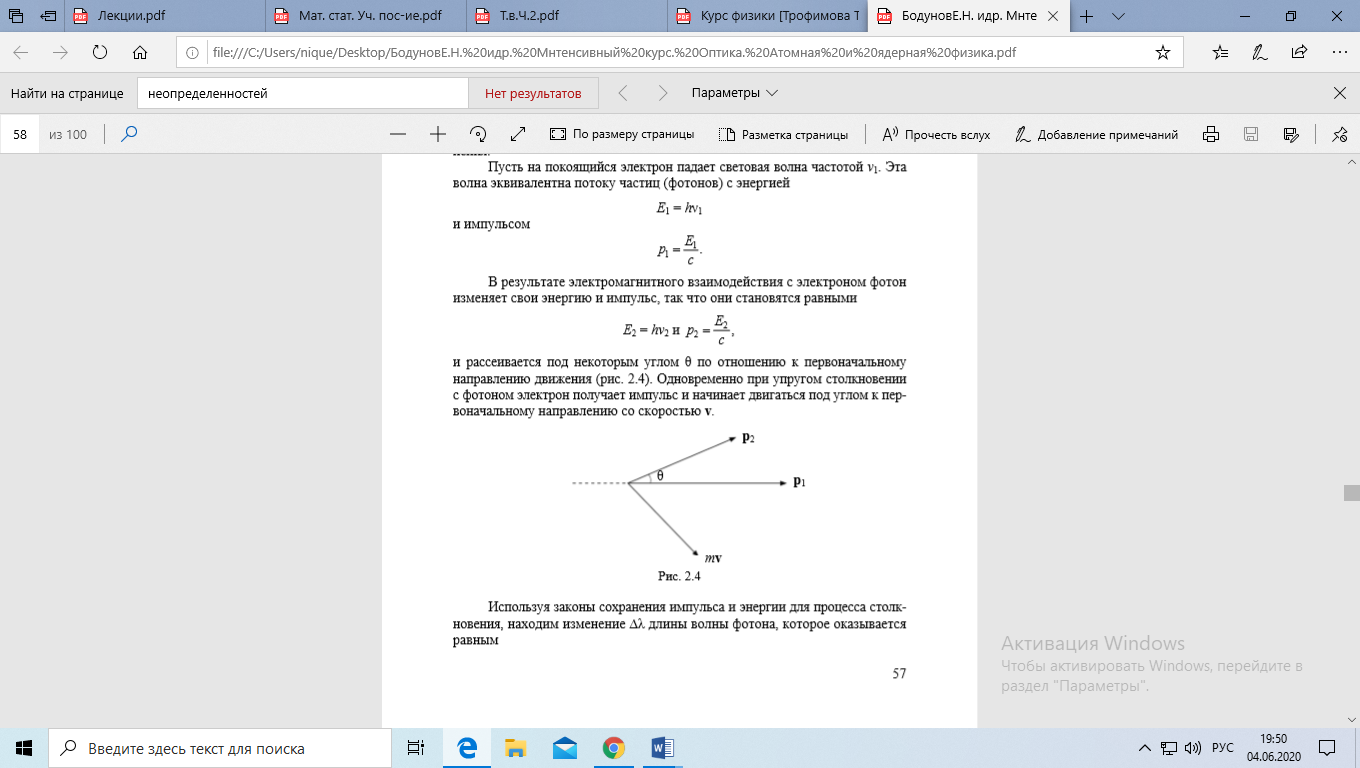
Используя законы сохранения импульса и энергии, находим изменение (увеличение) ∆λ длины волны фотона, которое оказывается равным ∆λ = λ2 – λ1 = λ_С (1 – cosθ).

Θ – угол рассеивания. Величина λ_С = h/mc = 0,0243 * 10^-10 м называется комптоновской длиной волны электрона – параметр элементарной частицы: величина размерности длины, характерная для квантовых процессов, идущих с участием этой частицы.

27. Волны Де-Бройля. Опыт Девиссона и Джермера по рассеянию электронов на монокристаллах

никеля.

Гипотеза о корпускулярно –волновом дуализме электромагнитного излучения гласит, что не только фотоны, но и электроны, а также любые другие частицы материи наряду с корпускулярными свойствами обладают и волновыми. Таким образом, с каждой частицей связаны, с одной стороны, корпускулярные характеристики (энергия E, импульс p), а с другой – волновые характеристики (частота ν, длина волны λ).

Согласно гипотезе де Бройля частице, имеющей импульс р, соответствует волновой процесс с длиной волны λ = h/p. Эта формула определяет длину волны де Бройля. Частица с массой m, движущаяся со скоростью v << c, имеет длину волны де Бройля λ = h/mv.

Первое экспериментальное подтверждение гипотезы де Бройля было получено К. Девиссоном и Л. Джермером. Они обнаружили, что пучок электронов, рассеиваясь на кристалле никеля, дает дифракционную картину, совпадающую с картиной рассеяния на кристалле коротковолнового рентгеновского излучения. Кристалл никеля в этих экспериментах играл роль дифракционной решетки. По положению дифракционных максимумов была определена длина волны электронов, которая соответствовала ее длине, вычисленной по формуле де Бройля.

Доказательство существования волновых свойств микрочастиц привело к выводу, что это – универсальное свойство материи. Таким образом, волновыми свойствами должны обладать и макроскопические тела. Однако вследствие большой массы макроскопических тел их волновые свойства не могут быть обнаружены экспериментально. Например, пылинка массой 10^–9 г, движущаяся со скоростью 0,5 м/с, имеет длину волны де Бройля порядка 10^–21 м, что на одиннадцать порядков меньше размеров атомов. Такая длина волны лежит в области, не доступной для наблюдения. Следовательно, макроскопические тела могут проявлять только корпускулярные свойства.