Интенсивный курс физики

Подставляя в это выражение значение В1, получаем

dF1 0 2I1I2 dl. 4 R

Аналогичные рассуждения показывают, что сила dF2, с которой маг-

нитное поле тока I2 действует на элемент dl первого проводника, направлена

в противоположную сторону и равна

dF2 I1B2dl 0 2I1I2 dl. 4 R

Таким образом, параллельные токи одинакового направления притягиваются друг к другу с силой

dF1 dF2 0 2I1I2 dl. 4 R

Можно показать, что между проводниками с токами противоположного направления действуют силы отталкивания.

3.7. Контур с током в магнитном поле

Магнитный момент тока. Во многих случаях приходится иметь дело с замкнутыми токами, размеры которых малы по сравнению с расстоянием

от них до точки наблюдения. Такие токи называют элементарными. Приме-

ром подобных токов могут служить электроны, движущиеся по замкнутым

орбитам.

Рассмотрим плоский контур – круговой виток радиусом R (рис. 3.13),

по которому течет ток I. Магнитные свойства такого контура описываются

векторной величиной pm, называемой магнитным моментом: pm ISn,

где S – площадь витка; n – вектор нормали к его плоскости.

R

В

pm

Рис. 3.13

70

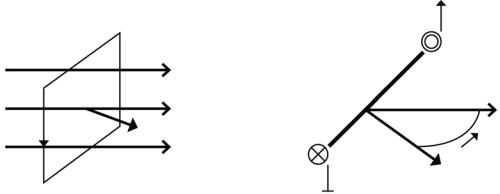
В теории магнетизма магнитный момент кругового витка с током играет такую же важную роль, как и электрический дипольный момент в теории электричества.

Момент сил, действующих на контур с током в магнитном поле.

Поместим в однородное магнитное поле с индукцией B плоский прямоугольный контур (рамку) с током (рис. 3.14, а) и вычислим момент сил, который на

нее действует.

F

Рис. 3.14

Согласнозакону Амперана каждый элемент токарамки действует сила dF I[dl,B].

Результирующая всех этих сил, как нетрудно убедиться, создает пару сил F и –F (рис. 3.14, б), стремящихся развернуть плоскость рамки перпендикулярно силовым линиям магнитного поля. Если a – длина короткой стороны рамки, то величина действующей на нее силы

M IBab IBS sin ,

где S = ab – площадь рамки.

71

Учитывая, что магнитный момент рамки pm ISn , последнюю формулу можно переписать в векторном виде:

M [pm ,B].

Момент пары сил М = 0, если pm и B параллельны, он максимален при

pm B .

Энергия контура с током в магнитном поле. Контур с током, поме-

щенный в магнитное поле, обладает запасом энергии. Действительно, чтобы повернуть контур с током на некоторый угол d , необходимо совершить работу против пары сил, действующих на этот контур со стороны поля. По величине эта работа равна

dA Md pmBsin d .

Совершенная над контуром работа расходуется на увеличение его энергии. Следовательно, запасенная контуром энергия будет равна

W2 Md 2 pmBsin d pmB cos

(при выводе этой формулы мы приняли, что при / 2 энергия контура W, определяемая с точностью до произвольной постоянной, равна нулю). Полученную формулу можно записать также в векторном виде:

W pmB.

Из последней формулы следует, что устойчивому положению равновесия контура с током в магнитном поле (положению с наименьшей энергией) соответствует его ориентация, при которой векторы pm и B параллельны (α = 0). В этом случае энергия контура минимальна и равна

W pmB 0.

Неустойчивому положению равновесия соответствует ориентация, при которой векторы pm и B антипараллельны (α = π). В этом случае энергия кон-

тура максимальна и равна

WpmB 0.

3.8.Циркуляция вектора магнитной индукции в вакууме.

Закон полного тока

Циркуляцией вектора B по замкнутому контуру L произвольной формы называется интеграл вида

72

Bdl Bldl,

L L

где dl – вектор элементарной длины контура (его направление совпадает с направлением обхода контура); Bl = Bcos – проекция вектора B на направление касательной к контуру; – угол между векторами B и dl.

С помощью понятия циркуляции формулируется закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора B): циркуляция вектора B по произвольному замкнутому контуру равна произведению магнитной постоянной 0 на алгебраическую сумму токов, охватываемых этим контуром:

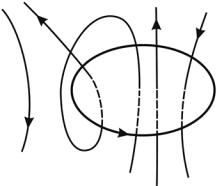
где n – число проводников с токами, которые охватываются контуром L. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Ток считается положительным, если его направление образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления – отрицательный. Например, для системы токов, изображенных на рис. 3.15,

Рис. 3.15

Закон полного тока справедлив только для поля в вакууме. Для поля в веществе необходимо учитывать еще и молекулярные токи.

Воспользуемся теоремой о циркуляции вектора B для расчета магнитного поля прямого тока I, перпендикулярного плоскости чертежа и направленного к нам (рис. 3.16). Представим себе замкнутый контур L в виде окружности радиусом r. В каждой точке этого контура вектор B одинаков по мо-

73

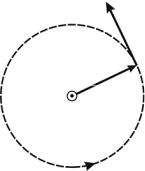
дулю и направлен по касательной к окружности (она совпадает с линией магнитной индукции). Следовательно, циркуляцию вектора B можно вычислить следующим образом:

Bl dl Bdl B dl B 2 r.

L L L

B

r

I

Рис. 3.16

Выбранный контур L охватывает ток I, поэтому по теореме о циркуля-

ции

В·2 r = 0I,

откуда модуль вектора магнитной индукции

B0I , 2 r

что совпадает с результатом, полученным с помощью закона Био–Савара– Лапласа.

Сравнивая выражения циркуляций векторов E и B, видим, что между ними существует принципиальное различие. Циркуляция вектора E электростатического поля всегда равна нулю, т. е. электростатическое поле является потенциальным. Циркуляция вектора B магнитного поля не равна нулю. Поле, циркуляция которого по замкнутому контуру отлична от нуля, называ-

ется вихревым.

3.9. Магнитное поле соленоида и тороида

Теорема о циркуляции вектора магнитной индукции позволяет находить индукцию магнитного поля без помощи закона Био–Савара–Лапласа.

74

Магнитное поле на оси прямого длинного соленоида. Соленоид –

это катушка, намотанная на цилиндрический каркас. Если длина соленоида намного больше его диаметра, то такой соленоид называют длинным. Магнитное поле максимально внутри соленоида и направлено вдоль его оси. Вблизи оси соленоида его магнитноеполе можно считать однородным.

Для нахождения индукции магнитного поля на оси прямого длинного соленоида с помощью теоремы о циркуляции магнитного поля выберем контур L, какпоказано на рис. 3.17.

H

На участке 1–2 направление магнитного поля совпадает с направлением обхода контура, а его индукция постоянна в силу однородности поля. На участках 2–3 и 4–1 вне соленоида проекция магнитного поля на направление обхода равна нулю. Наконец, на участке 3–4, удаленном на достаточно большое расстояние от соленоида, можно считать, что магнитное поле отсутствует.

Таким образом, циркуляция вектора магнитной индукции по всему выбранному контуру интегрирования

Поскольку согласно теореме о циркуляции вектора магнитной индукции этот интеграл равен 0 NI , где N – число витков соленоида, пронизыва-

ющих контур интегрирования, имеем

75

Bl 0IN,

откуда находим

B 0lNI 0In,

где n Nl – число витков, приходящихся на единицу длины соленоида.

Последняя формула получена в предположении, что соленоид находится в вакууме. Если пространство внутри соленоида заполнено веществом с магнитной проницаемостью (в соленоид введен сердечник), то поле внут-

ри него будет отличаться в раз, т. е.

B 0In.

Магнитное поле на оси тороида. Тороид – это катушка, намотанная на каркас, имеющий форму тора. Магнитное поле тороида целиком сосредоточено внутри него и неоднородно.

Для нахождения напряженности магнитного поля вблизи оси тороида применим теорему о циркуляции магнитного поля, выбрав контур L в виде окружности радиусом R (рис. 3.18). Имеем

R

I

I

Рис. 3.18

Вместе с тем этот интеграл равен 0 NI (N – общее число витков тороида), откуда следует, что

B 0 NI . 2 R

76

Если пространство внутри тороида заполнено веществом с магнитной проницаемостью , индукция магнитного поля будет равна

B 0 NI . 2 R

3.10. Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля

Элементарным потоком вектора магнитной индукции (элементарным магнитным потоком) через элементарную площадку dS называется физическая величина, равная

d B BdS BndS,

где Bn=В cos – проекция вектора В на направление нормали к площадке dS;– угол между векторами n и B; dS dSn – вектор, модуль которого равен dS, а направление совпадает с направлением нормали n к площадке.

Поток вектора B – скалярная физическая величина. Он может быть как положительным, так и отрицательным в зависимости от знака cos .

Поток вектора магнитной индукции ФB через произвольную поверхность S равен

B BdS BndS.

S S

Единицей измерения магнитного потока служит вебер (Вб): 1 Вб – магнитный поток, проходящий через плоскую поверхность площадью 1 м2, расположенную перпендикулярно вектору B, модуль которого равен 1 Тл

(1 Вб = 1 Тл м2).

Аналогично теореме Гаусса для электростатического поля можно доказать теорему Гаусса для поля В: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

BdS BndS 0.

S S

Эта теорема – следствие отсутствия магнитных зарядов, в результате чего линии магнитной индукции являются замкнутыми.

Используя теорему Гаусса, рассчитаем поток вектора B через соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником, магнитная проницаемость которого , равна

77

B 0I Nl .

Магнитный поток через один виток соленоида площадью S равен

B BS.

Полный магнитный поток, сцепленный со всеми его N витками, называемый потокосцеплением, в N раз больше:

B N NBS 0 Nl2I S.

3.11.Работа по перемещению проводника и контура с током в магнитном поле

Рассмотрим прямолинейный проводник длиной l с током I, который может свободно перемещаться вдоль параллельных проводников (рис. 3.19). В магнитном поле на проводник действует сила Ампера, модуль которой

F IBl,

так как вектор В перпендикулярен направлению в нем тока (на рис. 3.19 вектор В перпендикулярен плоскости чертежа).

dx

I

1 2

Рис. 3.19

Пусть под действием этой силы проводник переместится параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, совершаемая при этом силой Ампера, равна

dA Fdx IBldx IBdS Id B .

78

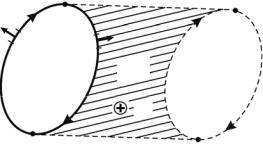
Так как ldx = dS – площадь, пересекаемая проводником при его перемещении в магнитном поле, BdS = dФВ – поток вектора магнитной индукции, пронизывающий эту площадь, имеем

dA Id B ,

т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Полученная формула справедлива для произвольного направления вектора В и произвольной формы проводника.

Вычислим работу по перемещению замкнутого контура с постоянным током I в магнитном поле из положения М (сплошная линия на рис. 3.20) в положение М (штриховая линия) в результате бесконечно малого перемещения. Ток в контуре направлен по часовой стрелке, магнитное поле – перпендикулярно плоскости чертежа. Контур М разобьем на два проводника:

AВС и CDА.

Работа dA, совершаемая силами Ампера при перемещении контура, равна алгебраической сумме работы по перемещению проводников AВС (dA1)

и CDA (dA2), т. е.

dA = dA1 + dA2.

Проводник CDA пересекает при движении магнитный поток dФ0 через заштрихованную поверхность и поток dФ2, пронизывающий контур в положении М . Следовательно, работа по перемещению проводника CDA в положениеC D A равна

dA2 I (d 0 d 2 ).

Проводник AВС при перемещении в положение А В С пересекает поток dФ0 через заштрихованную поверхность и поток dФ1, пронизывающий контур в положении М. Силы Ампера, действующие на этот проводник, совершают отрицательную работу

79