Интенсивный курс физики

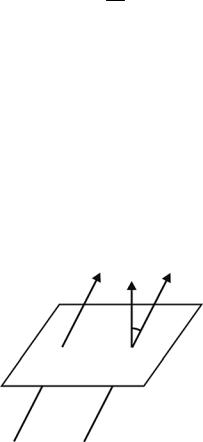
EB = EA / 2.

В произвольной точке пространства, расположенной на расстоянии r от диполя, напряженность E всегда пропорциональна p и обратно пропорциональна r3:

E rp3 ,

где – знак пропорциональности.

1.5. Поток вектора напряженности

Потоком вектора напряженности E однородного электрического поля через плоскую площадку S называется величина (рис.1.4)

ФE E S cos .

n E

α

S

Рис. 1.4

Здесь n – нормаль к площадке; α – угол между векторами n и E. Если поле неоднородно или поверхность, с помощью которой вычис-

ляется поток, не является плоской (рис. 1.5), определение его потока следует применить к бесконечно малому элементу поверхности dS, а именно, записать элементарный поток в виде

dФЕ EdS cos EndS.

Тогда поток через конечную поверхность S определяется интегралом

ФЕ EndS EndS,

S S

10

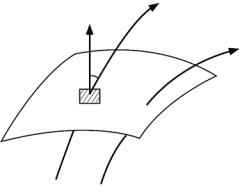
где En E cos – проекция вектора напряженности на нормаль в данной точке поверхности.

n E

E

α S

dS

Рис. 1.5

Поток вектора напряженности E является алгебраической величиной. Знак его зависит от выбора направления нормали к элементарным площадкам, на которые разбивается поверхность S при вычислении ФЕ. Изменение направления нормали на противоположное изменит знак Encosα, а значит, и знак потока ФЕ. В случае замкнутых поверхностей знак потока принято считать положительным, если силовые линии поля выходят из охватываемой области. Поток пропорционален числу силовых линий, пересекающих данную поверхность. Размерность потока в СИ вольт на метр (В·м).

1.6. Теорема Гаусса

Напряженность электрического поля системы электрических зарядов можно вычислить с помощью принципа суперпозиции. Эти вычисления значительно упрощаются при использовании теоремы Гаусса, которая связывает поток вектора напряженности электрического поля через произвольную замкнутую поверхность с величиной заряда внутри этой поверхности.

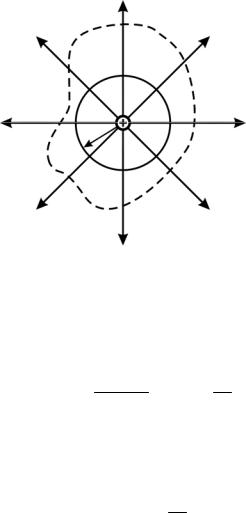
Вычислим поток вектора напряженности через сферическую поверхность радиусом r, охватывающую точечный заряд q, находящийся в ее цен-

тре (рис. 1.6).

Нормаль n к замкнутой поверхности всегда выбирается внешней. Так как на всей сферической поверхности напряженность поля точечного заряда постоянна и вектор напряженности направлен перпендикулярно этой поверхности, поток равен

ФЕ EndS ES.

S

11

q

r

Рис. 1.6

Напряженностьполя точечного заряда E q / (4 0r2 ), площадь сфери-

ческой поверхности S 4 r2. Таким образом,

ФЕ ES 4 q0r2 4 r2 q0 .

Этот результат справедлив для замкнутой поверхности любой формы (на рис. 1.6 она изображена штриховой кривой), т. е.

ФЕ EndS q .

S 0

Интеграл означает, что интегрирование ведется по замкнутой по-

верхности S. Знак потока совпадает со знаком заряда q.

Если произвольная поверхность охватывает систему из n точечных зарядов qi, то в соответствии с принципом суперпозиции напряженность поля, создаваемого зарядами, равна сумме напряженностей полей, создаваемых каждым зарядом в отдельности. Поэтому суммарный поток вектора напряженности через эту поверхность

Эта формула является аналитической записью теоремы Гаусса для электростатического поля: поток вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 0.

12

Если электрические заряды распределены непрерывно с некоторой объемной плотностью ( = dq/dV – заряд, приходящийся на единицу объема), разной в разных областях пространства, то суммарный заряд внутри замкнутой поверхности S, охватывающей некоторый объем V, определяется интегрированием:

qi dV.

i V

Интегрирование проводится по всему объему, в котором распределены заряды. В этом случае теорема Гаусса записывается в виде

ФЕ EndS 1 dV.

S 0 V

1.7. Применение теоремы Гаусса для расчета напряженности электростатических полей

Теорема Гаусса помогает найти напряженность полей, создаваемую системой симметрично распределенных зарядов. Для этого необходимо подобрать такую замкнутую поверхность, охватывающую заряды, чтобы вычисление потока вектора напряженности через эту поверхность сводилось к простым алгебраическим операциям.

Напряженность поля бесконечной равномерно заряженной плоско-

сти. Пусть бесконечная плоскость (рис. 1.7) заряжена с постоянной поверхностной плотностью + ( = dq/dS – заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны.

E

S

Рис. 1.7

В качестве замкнутой поверхности выберем поверхность цилиндра, основания которого параллельны заряженной плоскости. В этом случае об-

13

разующие цилиндра параллельны линиям напряженности, поток вектора напряженности через его боковую поверхность равен нулю, а полный поток через него – сумме потоков через его основания (площади оснований цилиндров S равны, и на них напряженность Еn совпадает с напряженностью Е), т. е. 2ES. Заряд, заключенныйвнутрицилиндра, равен S.

Согласно теореме Гаусса

2ES S ,

0

откуда следует, что

E . 2 0

Таким образом, напряженность поля на любом расстоянии от заряженной плоскости одинакова по величине и направлению с каждой стороны этой плоскости, иными словами, поле равномерно заряженной бесконечной плоскости однородно.

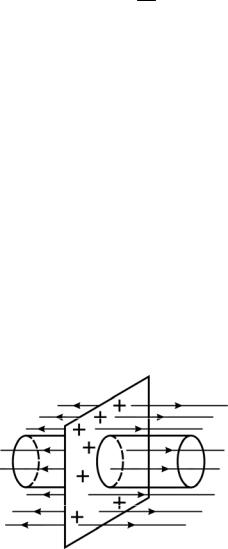
Поле двух бесконечных параллельных разноименно заряженных плоскостей. Напряженность такого поля вычисляется как суперпозиция полей, создаваемых каждой плоскостью в отдельности. Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотно-

стями + и – .

Рис. 1.8

Верхние стрелки на рис. 1.8 – силовые линии поля положительно заряженной плоскости, нижние – отрицательно заряженной. Слева и справа от плоскостей силовые линии направлены навстречу друг другу, поэтому напряженность поля E = 0. В области между плоскостями направления силовых линий совпадают, напряженность полей складывается, в результате между пластинами имеем

14

E .

0

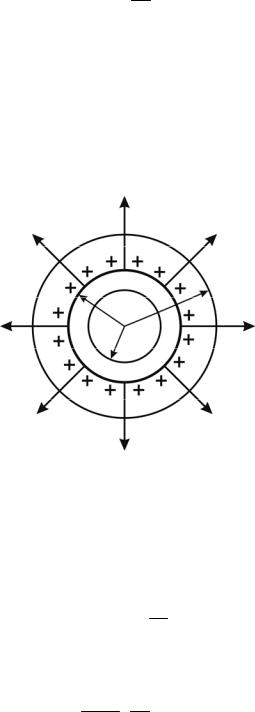
Поле равномерно заряженной сферической поверхности. Пусть сфе-

рическая поверхность радиусом R заряжена равномерно с поверхностной плотностью + и суммарным зарядом q. Электрическое поле такой поверхности обладает сферической симметрией: напряженность E одинакова на одинаковом расстоянии от центра сферы, а линии напряженности направлены вдоль ее радиусов (рис. 1.9).

R r

r

Рис. 1.9

В качестве замкнутой поверхности выберем поверхность сферы радиусом r, имеющую общий центр с заряженной сферой. Если r > R, внутри поверхности находится весь заряд q, создающий электрическое поле, и по теореме Гаусса

4 r2E q ,

0

откуда получаем

E 4 1 0 rq2 , r R.

При r > R напряженность электрического поля убывает с увеличением расстояния r по тому же закону, что и у точечного заряда.

Если rʹ < R, замкнутая поверхность не содержит зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E = 0).

15

Зависимость напряженности поля Е от r приведена на рис. 1.10.

Е

1

r2

Рис. 1.10

Поле объемно заряженного шара. Шар радиусом R с общим зарядом q заряжен равномерно с объемной плотностью . Как и в случае с заряженной сферической поверхностью, распределение заряда сферически симметрично. Можно показать, что напряженность поля вне шара совпадает с напряженностью его равномерно заряженной сферической поверхности.

Найдем напряженность поля внутри шара. Сфера радиусом r' < R охватывает заряд

q 43 r 3 .

Е

Поэтому согласно теореме Гаусса

E 4 r2E q ' 4 r 3 .

0 3 0

16

Таким образом, напряженность поля внутри равномерно заряженного шара увеличивается прямо пропорционально расстоянию от его центра.

Зависимость напряженности поля Е от r для рассмотренного случая приведена на рис. 1.11.

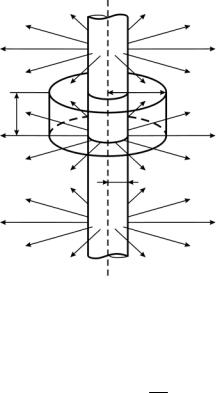
Поле равномерно заряженного бесконечного цилиндра. Пусть бес-

конечный цилиндр радиусом R (рис. 1.12) заряжен равномерно с линейной плотностью заряда ( = dqdl – заряд, приходящийся на единицу длины).

Всилу цилиндрической симметрии линии напряженности электрического поля перпендикулярны поверхности цилиндра. В качестве замкнутой поверхности выберем поверхность цилиндра (коаксиального с заряженным) радиусом r и высотой l. Поток вектора E через торцы этого цилиндра равен нулю (торцы параллельны линиям напряженности), а через боковую поверхность –

2 rlЕ.

Е

r

l

R

Рис. 1.12

По теореме Гаусса при r > R

E 2 rlE l ,

0

17

откуда следует, что

Эта формула справедлива также и для равномерно заряженной прямолинейной нити.

Если r < R, замкнутая поверхность зарядов внутри не содержит, и в этой области E = 0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра обратно пропорциональна расстоянию до его оси. Внутри заряженного цилиндра поле отсутствует.

1.8. Потенциал. Разность потенциалов. Работа сил электростатического поля

Работа, совершаемая электростатическими силами при перемещении заряда q из одной точки поля в другую, зависит только от начального и конечного положения заряда в этом поле. Из механики известно, что такие силы являются потенциальными. Следовательно, заряд, помещенный в электростатическое поле, обладает потенциальной энергией.

Энергетической характеристикой электрического поля является потенциал.

Потенциалом поля называется скалярная физическая величина, численно равная потенциальной энергии единичного положительного заряда, внесенногов данную точку поля:

Wп , q0

где Wп – потенциальная энергия заряда q0 в данной точке поля.

Любой заряд q, внесенный в точку поля с потенциалом , обладает потенциальной энергией

Wп q .

Так как электростатическое поле является потенциальным, работа, совершаемая силами этого поля при перемещении заряда q между его точками с потенциалами 1 и 2, равна изменению потенциальной энергии такого заряда, взятому с противоположным знаком:

A12 Wп2 Wп1 Wп1 Wп2.

18

С учетом того, что Wп1 q 1, а Wп2 q 2 ,

A12 q 1 2 ,

где 1 2 – разность потенциалов.

Разностью потенциалов называется физическая скалярная величина, численно равная работе, совершаемой полем при перемещении единичного положительного заряда между точками с потенциалами 1 и 2:

1 2 A12 . q0

Если силы электростатического поля перемещают заряд q из точки 1 в бесконечно удаленную точку, в которой Wп1 0 и соответственно 0, то

1 A1 . q0

Отсюда следует, что потенциал в данной точке электростатического поля численно равен работе, которую необходимо совершить для перемещения единичного положительного заряда из данной точки в бесконечность.

В системе СИ потенциал (разность потенциалов) измеряется в вольтах (В): 1 В = 1 Дж/Кл.

Потенциал поля зависит от значения зарядов, создающих поле, положения данной точки по отношению к зарядам и электрических свойств среды. Потенциал поля, созданного точечным зарядом q в точке, отстоящей от заряда на расстояние r, равен

где ε – диэлектрическая проницаемость среды.

Потенциал электростатического поля шара радиусом R с зарядом q, равномерно распределенным по поверхности, вне шара совпадает с потенциалом точечного заряда q, помещенного в центре шара.

Геометрическое место точек электрического поля, в которых потенциал имеет одинаковое значение, называется эквипотенциальной поверхностью

(или линией).

Потенциал электростатического поля, созданного системой n электрических зарядов, равен алгебраической сумме потенциалов, создаваемых каждым зарядом в отдельности:

n

1 2 ... n i.

i 1

19