Вопрос 34 Реализация комбинационных схем в базисе Жегалкина («и», «искл. Или», «1»).

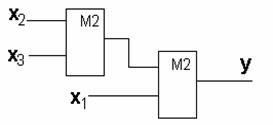
Упрощенным подходом к построению схемы в базисе (И, М2) является преобразование схемы из сокращенного булева базиса (И, НЕ) в базис Жегалкина. Для этой цели инверторы (элементы НЕ) заменяются двухвходовыми элементами М2, реализующими операции сложения по модулю два.

Другим, более сложным, подходом является преобразование аналитического выражения для булева базиса в базис Жегалкина путем замены операций дизъюнкции и отрицания операциями конъюнкции и сложения по модулю два. При этом в целях сокращения достаточно громоздких преобразований в качестве исходного выражения целесообразно выбирать то, в к-ом используется меньшее число членов в операциях дизъюнкции.

¬x=1(+)x

x\/y=x(+)y(+)xy

Вопрос 35 Реализация комбинационных схем в базисах «и-не», «2и-не», оценка сложности.

Реализация КС на базисе И-НЕ, 2И-НЕ

При синтезе схем в базисе И-НЕ минимизация булевых функций проводится следующим образом:

1. Строятся минимальные ДНФ булевых функций;

2. Минимизируется число инверсий входных переменных на основе правила

3. Перевод ПФ в базис И-НЕ производится по представлению  минимальной ДНФ

   - заменой всех дизъюнкций по правилу

   - заменой конъюнкций (без инверсий) по правилу

   - заменой одной из двойных инверсий по правилу

    

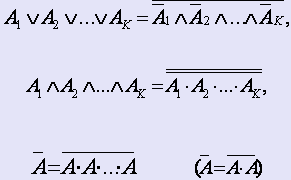
Для реализации КС на элементах 2И-НЕ удобно пользоваться логической функцией Шеффера.

При этом заданная ПФ переводится в указанный базис по правилам:

- выделяются скобками пары дизъюнкций и конъюнкций (предпочтительным является выделение сочетаний одинаковых букв в разных элементарных конъюнкциях)

   - заменяются пары дизъюнкций конъюнкциями

   - заменяются пары конъюнкций

   - исключаются двойные отрицания

Вопрос 36 Реализация комбинационных схем в базисах «или-не», «2или-не», оценка сложности

Для перехода к базису ИЛИ-НЕ в минимальной КНФ функции производится

   - замена всех конъюнкций по правилу

   - замена всех дизъюнкций (без инверсий)

 Для перевода ПФ в базис 2ИЛИ-НЕ рекомендуется пользоваться логической функцией Пирса  [3] и следующей последовательностью действий:

- выделить скобками пары дизъюнкций и конъюнкций в представлении ПФ в виде КНФ

- заменить пары конъюнкций

- заменить пары дизъюнкций

-исключить двойные отрицания  и заменить одиночные отрицания

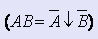
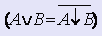
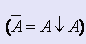
Сложность схемы оценивается количеством оборудования, составляющего схему. При разработке схем количество оборудования обычно измеряется числом корпусов (модулей), используемых в схеме. В теоретических разработках ориентируются на произвольную элементную базу и поэтому для оценки затрат оборудования используется оценка сложности по Квайну.

Сложность (цена) схемы по Квайну определяется суммарным числом входов логических элементов в составе схемы. При этом цена инверсного входа обычно принимается равной двум.

∑(от ш=1 до k) l*m, где m-число входов, l-число эл-тов, k-число логических эл-тов

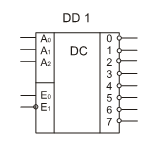
Вопрос 37 Реализация комбинационных схем на дешифраторах

Дешифратор (decoder) - устр-во, относящиеся к классу КС, преобразующее позиционный двоичный код в унитарный.

Дешифратор (DС) позволяет определить, в каком состоянии находится цифровое устройство . Дешифратор на входе имеет n переменных,а на выходе 2n функций.

Т.к на выходах DC присутствуют все компоненты наборов переменных в виде их конъюнкций,то синтез схем на DC сводится к тому,чтобы поставить на выходе DC схему ИЛИ,функцию представить в виде ДСНФ и объединить соответствующие выходы DC на входах схемы ИЛИ.