
16
замкнутой, т.е. когда она ограничивает некоторое тело, то имеется внутренняя сторона, обращенная к телу, и внешняя сторона, обращенная к окружающему пространству.
Все эти поверхности можно назвать двусторонними поверхностями. Однако существуют и так называемые односторонние поверхности, т.е. поверхности, имеющие только одну сторону.
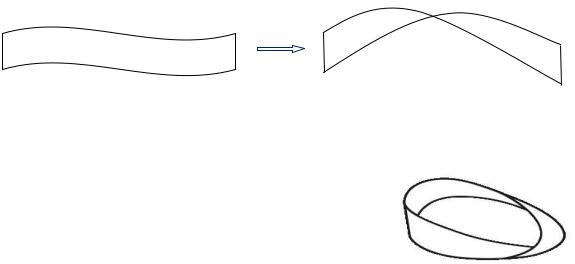
Классическим примером односторонней поверхности является так называемый лист Мебиуса. Его модель можно получить следующим способом.
Надо взять прямоугольный кусок 1 1 какой-нибудь материи (бумаги, ленты и т.д.) и, перекрутив этот кусок один раз, склеить его концы (точку с 1, точку с 1) - так, как показано на рисунке (рис. 3.16).
|
1 |
|
|
|
|
|
|
|
1 |
||
|
|
|
|
||
|
1 |
|
|
1 |
|
|
|
|
|
||
Рис. 3.16. Схема получения листа Мебиуса |
|
|
|||
В результате получим перекрученное кольцо, которое и называется лист Мебиуса |
|||||
(рис. 3.17). Эта поверхность обладает следующим |
|
|
|
||
парадоксальным свойством: если ее начать красить |
|
|
|
||
в какой-либо цвет, то можно, не переходя на другую |
|
|
|
||
«сторону поверхности», тем не менее, покрасить |
|
|
|
||
«обе стороны» поверхности этим цветом. |
|
|
|
|
|
Это говорит о том, что у данной поверхности |
|
|
|
||
Рис. 3.17. Изображение листа |
|
||||
|
|
|
|
||
всего одна сторона. |
|
|
Мебиуса |
|
|
Дадим определение односторонней поверхности. |
|
|
|
||
|
|
|
|||
Выберем некую точку 0 |
на поверхности и проведем через точку |
0 |
|||
замкнутый контур, лежащий на этой поверхности (не пересекающий ее границу). В каждой точке этого контура проведем нормаль к данной поверхности.
Пусть точка вместе со своей нормалью обходит этот контур, начиная движение из точки 0; при этом подразумевается, что вектор нормали меняет свое направление непрерывно по мере движения по контуру.
После обхода контура и возвращения в точку 0 направление вектора нормали может оказаться таким же, как и в начале пути, или же стать противоположным по отношению к исходному направлению.
Определение 3.11.
Гладкая поверхность называется односторонней, если на ней существуют точка0 и контур, проходящий через эту точку – такие, что при обходе контура направление вектора нормали меняется на противоположное направление.
Определение 3.12.
Гладкая поверхность называется двусторонней, если для любых ее точек 0 и любого содержащего эту точку контура направление вектора нормали сохраняется при обходе контура.
В дальнейшем мы исключим из рассмотрения односторонние поверхности. Все поверхности, о которых пойдет речь далее, считаются двусторонними.
17
На этих поверхностях фиксируется одна из сторон поверхности путем указания направления вектора нормали. Тем самым вводится определенная ориентация на данной поверхности. Сама поверхность при этом называется ориентированной.
3.3.2. Понятие потока вектора через поверхность |
|
|
|||
Рассмотрим поверхность , через которую |
|
|
|
||
перемещаются (проходят, перетекают) частицы |
|
|
|
||
|
|
|
|
|
|
некоторого вещества произвольной природы |
|
|
|
( ) |
|
|
|
|
|
||
(например, газа или жидкости). |
|
|
|
|
|
|
|
|
|
|
|
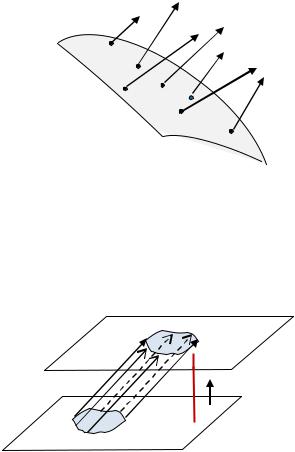
Пусть это движение задается вектором ( ), |
|
||||
который определяет величину и направление |
|
|
|
|
|
скорости частиц в каждой точке поверхности |
|
|
|
||
(рис. 3.18). |
|
|
|
|
|
Определение 3.13. |
|
|
Рис. 3.18. К понятию потока |
||
|
|
|
|||
|
|
|
|
|
|
Потоком П вектор-функции ( ) через |
вектора через поверхность |
||||
|
|
|
|||
поверхность называется общее количество (объем) |
|
|
|
||
|
|
через эту поверхность за единицу времени. |
|||
вещества, протекающего со скоростью ( ) |
|||||
Задача (о вычислении потока). |
|
|
|
|
|
|
|
через заданную поверхность . |
|
||
Найти поток П вектор-функции ( ) |
|
||||
Решение. |
|
|
|
|
|
Если поверхность - плоская, а |
|
|
|
|
|
|
|
|
|
|
|
вектор-функция ( ) - постоянная: ( ) = , |
|
|
|
||
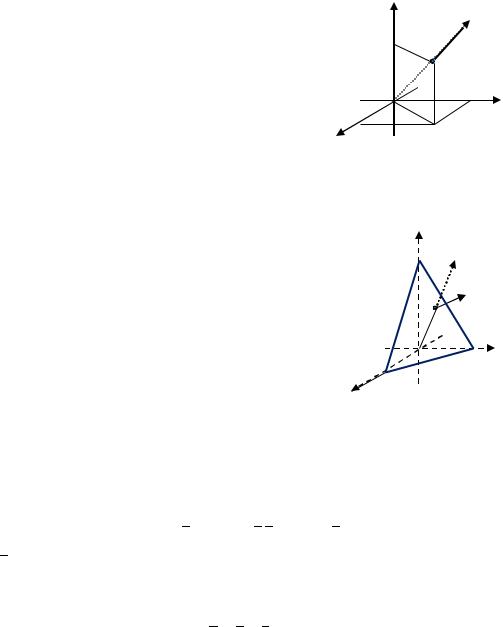
то за единицу времени частицы, проходящие |
|
|
|
0 |
|
через эту поверхность, заполнят |
|
|
|
|
|
|
|
|
|
|
|
цилиндрическое тело с основанием и |
|
|
|
|
|
|
|
|
|
|
|
образующими, совпадающими с вектором |
|
|
|
|
|
(рис. 3.19). |
Рис. 3.19. К задаче о вычислении потока |
|
Значит, поток П в этом случае равен |
||
|
объему цилиндрического тела, т.е. произведению площади основания ( ) на высоту . Высота цилиндрического тела равна проекции вектора на единичный вектор
0 нормали к плоскости (рис. 3.19), т.е. скалярному произведению этих векторов. Таким образом, для рассматриваемого случая имеем следующее выражение для потока:
П = ( )∙ = ( )∙Пр 0 ( ) = ( )∙ ( )∙ 0.
Чтобы вычислить поток в общем случае, выполним следующие действия. 1. Разбиваем поверхность на частичные поверхности: = 1 2 … и
обозначаем площадь -й частичной поверхности через ∆ = ( ), = 1 ÷ .
2. В каждой части выбираем промежуточные точки и вычисляем значения
( ) и 0( ), = 1 ÷ .
Предполагаем, что диаметры частичных поверхностей настолько малы, что эти поверхности почти не отличаются от плоских фигур, а значения ( ) и 0( ) при значениях незначительно отличаются от значений ( ) и 0( ).
Тогда поток через поверхность приближенно равен: П ≈ ∆ ∙ ( )∙ 0( ),= 1 ÷ , а весь поток вычисляется приближенно по формуле:
18
П ≈ ∑=1 ( )∙ 0( )∙∆ .
Эта приближенная формула тем точнее, чем меньше размеры частичных
поверхностей , = 1 ÷ , т.е. чем меньше ранг разбиения λ = .
1≤ ≤
В пределе получаем точное значение:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∑=1 ( )∙ 0( )∙∆ . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ → 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Замечание 3.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Поток удовлетворяет свойству аддитивности: если = 1 2, |
1 ∩ 2 = , то |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
П = П |
+ П , где П |
|
|
- поток через поверхность , |
= 1, 2. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
3.3.3. Примеры на вычисление потока радиус-вектора |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рассмотрим примеры на вычисление потока радиус-вектора |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= ( ) = ( ) = ∙ + ∙ + ∙ (рис. 3.20) через различные поверхности. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
||||||
Найти поток П радиус-вектора через |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
часть плоскости |
: |
|
|
+ |
|
|
|
+ |
|
|
|
= 1 ( , , > 0), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
расположенную в первом октанте в направлении нормали, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
образующей острые углы с осями координат. |
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Применим формулу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
П = |
|
∑ |
|
|
|
|
( |
)∙ ( )∙∆ , |
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.20. Изображение |
|||||||||||||||||||||||||||||||||||||
|
|
λ → 0 |
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
( ) |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
радиус-вектора точки |
|||||||||||||||
= |
|
∙( |
|
+ |
|
|
|
+ |
|
|
|
|
) |
- единичный вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
0 |
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
нормали к плоскости (рис. 3.21), λ = √ |
1 |
|
+ |
1 |
+ |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
2 |
|
|
|
|
|
( ) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вычислим скалярные произведения векторов: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
( )∙ ( ) = |
1 |
∙( |
1 |
|
|
+ |
|
1 |
|
|
|
+ |
1 |
|
) = |
1 |
|
∙1 = |
1 |
, = 1 ÷ . |
|
|
|
|
|
|
|
|
0( ) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В результате получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
П = ∑ |
|
|
1 |
∙∆ |
|
= |
|
|
1 |
∙ ∑ |
∆ |
= |
1 |
∙( ), |
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
λ → 0 |
|
=1 λ |
|
|
|
|
|
|
|
|
|
|
λ |
|
|
λ → 0 |
=1 |
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
где ( ) – площадь треугольника с вершинами в точках |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
( ; 0; 0), (0; ; 0), (0; 0; ) (рис. 3.21). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Площадь треугольника можно вычислить по |
|
|
Рис. 3.21. К Примеру 3.6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
площади его проекции на плоскость (см. 3.1.2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
||
= ∙ γ, |
где γ - угол между векторами 0 {λ∙ ; |
λ∙ |
; λ∙} и |
{0; 0; 1}; |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
γ = |
|
| 0∙ | |
|
= |
|
|
|
( ) = = ∙λ∙ = |
λ∙ . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
λ∙ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
| 0|∙| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Следовательно, поток равен: П = 1λ∙ = 1λ∙12 λ∙ = 12 .
Ответ: П = 12 .
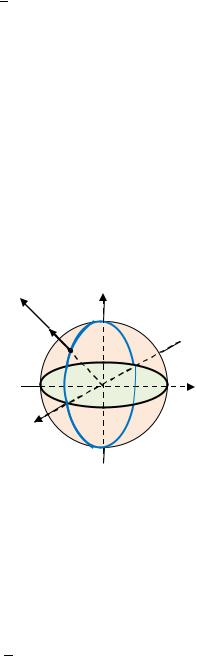
Пример 3.7.
Найти поток П радиус-вектора через поверхность тетраэдра, ограниченного координатными плоскостями и плоскостью + + = 1 ( , , > 0), в направлении внешней нормали.
19
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Поверхность тетраэдра состоит из 4-х граней: = 1 |
2 3 4, |
||||||||||||
|
|
|
|
|
|
|
|
+ |
|
+ |
|
= 1 |
|
где , |
|
, |
|
, |
: { |
|
|
|
|
}. |
|||
|
|
|
|
|
|
||||||||
1 |
2 |
|
3 |
|
4 |
≥ 0, ≥ 0, ≥ 0 |
|||||||
По свойству аддитивности потока имеем: П = П1 + П2 + П3 + П4, где П - поток через поверхность , = 1 ÷ 4. П4 = 12 (см. Пример 3.6).
Найдем потоки через поверхности (грани) 1, , 2, , 3. На поверхности 1 имеем:
0 |
|
|
( ){; ; 0}, 0( ){0; 0; −1} ( )∙ 0( ) = 0 |
1. |
|||||
( ) = − |
|||||||||
На поверхности 2 |
имеем: |
|
|
|
|
|
|||
0 |
( ) = − |
|
( ){ ; 0; }, 0( ){0; −1; 0} |
( )∙ 0( ) = 0 |
2. |
||||
На поверхности 3 |
имеем: |
|
|
|
|
|
|||
0 |
( ) = − |
|
( ){0; ; }, 0( ){−1; 0; 0} |
( )∙ 0( ) = 0 |
3. |
||||
Следовательно, получаем: П |
= П |
= П = 0 и П = 0 + 0 + 0 + П = |
1 |
. |
|||||
|
|||||||||
|
|
|
1 |
2 |
3 |
4 |
2 |
||
|
|
|
|
|
|
|
|||
Ответ: П = |
1 |
. |
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
Пример 3.8. |
|
|
|
|
|
|
|
|
|
Найти поток П радиус-вектора через сферу радиуса с центром в начале |
|||||||||
координат в направлении внешней нормали. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
( ) |
0 |
( ) |
|
|
|
|
|
|
|
|||
Применим формулу для потока: |
|
||||||||
|
|
|
|||||||
П = |
∑ |
( |
)∙ ( |
)∙∆ , |
|
|
|
||
λ → 0 |
|
=1 |
|
0 |
|
|
|
||
где 0( ) - единичный вектор нормали к поверхности сферы (рис. 3.22).
|
|
|
|
|
|
(градиент) |
|
|
Так как вектор нормали |
||||
к поверхности ( , , ) = 0 имеет вид (см. 3.1.4): |
||||||
|
′ |
( ), |
′ |
′ |
( )}, то из уравнения сферы |
|
{ |
|
|
( ), |
|||
|
|
|
|
|
|
|
2 |
+ 2 + 2 − 2 = 0 – получаем вектор нормали: |
|||||||
|
′ |
= 2, |
′ |
= 2, |
′ |
= 2 |
|
{2 ; 2 ; 2 }. |
|
|
|
|
|||||
|
|
|
|
|
|
|||
Рис. 3.22. К Примеру 3.8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Единичный вектор нормали с точностью до знака имеет вид: ( ) = ± |
|
|
= |
||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
= ± |
1 |
{2 ; 2 ; 2 } = ± |
1 |
{ ; ; } = ± |
1 |
{ ; ; } = ± |
1 |
( ), |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
√4 2+ 4 2+ 4 2 |
√ 2+ 2+ 2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
т.е. на поверхности сферы вектор 0( ) и радиус-вектор ( ) - коллинеарны. Учитывая, что нормаль должна быть внешняя, векторы 0( ) и ( ) должны
быть одинаково направлены: 0( ) ↑↑ ( ) 0( ) = 1 ( ).
Подставляя это значение 0( ) в формулу для потока, получим: |
|
|||||||||||||||
П = |
∑ |
( )∙ |
1 |
( |
)∙∆ |
= |
1 |
∙ |
∑ |
| |2( |
)∙∆ |
= |
1 |
∙ |
∑ |
2∙∆ = |
|
|
|
||||||||||||||
λ → 0 |
=1 |
|
|
|
|
|
λ → 0 |
=1 |
|
|
|
λ → 0 |
=1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
= ∙ |
∑ |
∆ = ∙( ) = ∙42 = 43. |
|
|
|
|
|
|
|
|||||||
λ → 0 |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
П = 43. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3.9.
Найти поток П радиус-вектора через прямой круговой цилиндр в направлении внешней нормали. Ось цилиндра совпадает с осью , высота равна , основание лежит

20
в плоскости и имеет радиус . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Поверхность цилиндра состоит из 3-х частей – двух оснований и боковой |
|
|
|||||||||||||||||||||||||||||||||||||||
поверхности: = 1 |
2 |
3, где 1 - нижнее основание, 2 - верхнее основание, |
||||||||||||||||||||||||||||||||||||||||
3 – боковая поверхность (рис. 3.23). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0( ) |
|
|||||||||||||||||||||||||
|
Поток через всю поверхность цилиндра равен |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сумме потоков через эти поверхности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
П = П1 + П2 + П3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0( ) |
||||||||||||||||
|
|
На поверхности |
|
{( , , ) 3: = 0} имеем: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0( ) |
|
|
|
|
|
|
( ){; ; 0}, 0( ){0; 0; −1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
( )∙ 0( ) = 0 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
П = |
∑ |
|
|
|
( |
)∙ ( |
)∙∆ |
= |
∑ |
0∙∆ |
= |
|
|
|
|
|
|
|
|
|
0 |
( ) |
|
|||||||||||||||||||
1 |
λ → 0 |
|
=1 |
|
|
|
0 |
|
|
|
|
|
|
|
λ → 0 |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= ∑ =1 0 = 0 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
λ → 0 |
|
|
|
|
|
|
|
|
λ → 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.23. К Примеру 3.9 |
||||||||||||||
|
|
На поверхности |
|
{( , , ) 3: = } имеем: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0( ) |
|
|
|
|
|
( ){; ; }, |
0( ){0; 0; 1} ( )∙ 0( ) = |
2. |
|
|
||||||||||||||||||||||||||||||||
= |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
П = |
∑ |
|
|
|
( |
)∙ ( |
)∙∆ |
= |
∑ |
∙∆ |
= ∙ |
∑ |
|
|
∆ = ∙( ) |
= |
||||||||||||||||||||||||||
2 |
λ |
→ 0 |
|
=1 |
|
|
|
|
0 |
|
|
|
|
λ → 0 |
=1 |
|
|
|
|
|
|
λ → 0 |
|
|
=1 |
|
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= ∙ 2 = 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
На поверхности |
|
{( , , ) 3: 2 + 2 |
= 2} имеем: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- вектор нормали (градиент) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
{2 ; 2 ; 0} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
( ) = ± |
|
|
|
= ± |
|
|
1 |
|
|
|
|
{2 ; 2 ; 0} = ± |
1 |
|
|
{; ; 0} = ± |
1 |
{; ; 0} |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
2 |
|
|
2 |
|
||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
√4 |
+ 4 |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
( )∙ ( ) = ± { ; ; }∙ |
1 |
{; ; 0} = ± |
1 |
∙(2 + 2) = ± |
1 |
∙ 2 = ±. |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Учитывая, что нормаль должна быть внешняя, угол между векторами 0( ) и |
|||||||||||||||||||||||||||||||||||||||||
( ) должен быть острым (рис. 3.23). Следовательно, имеем: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( )∙ 0( ) > 0 ( )∙ 0( ) = . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
П = |
∑ |
|
|
|
( |
)∙ ( |
)∙∆ |
= |
∑ |
∙∆ |
= ∙ |
∑ |
|
∆ |
= ∙( ) = = |
|||||||||||||||||||||||||||
3 |
λ |
→ 0 |
|
=1 |
|
|
|
|
0 |
|
|
|
|
λ → 0 |
=1 |
|
|
|
|
|
|
λ → 0 |
|
=1 |
|
|
|
|
3 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∙2 = 22 . |
Окончательно получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
П = П + П + П = 0 + 2 + 22 = 32 . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: П = 32 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
3.3.4. Понятие поверхностного интеграла 2 рода |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Рассмотрим гладкую ориентированную поверхность в пространстве (рис. 3.24), |
|||||||||||||||||||||||||||||||||||||||||
на которой задана вектор-функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
( ). |
|
|
|
|
|
|
|
|
0( ) |
|
|
|
||||||||||||||||||||||||||||||
|
|
Выполним следующие действия. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1. |
Разбиение поверхности : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
= |
|
|
… . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Выбор промежуточных точек: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
, |
= 1 ÷ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
Вычисление скалярных произведений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
векторов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( )∙ 0( ), = 1 ÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
и интегральной суммы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
= ∑ |
|
|
|
|
|
|
|
|
|
)∙∆ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
=1 |
( )∙ ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где ∆ |
|
= ( |
|
|
) |
– площадь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.24. Ориентированная поверхность |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
21 |
частичной поверхности , |
= 1 ÷ . |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Если ввести обозначение: |
|
|
|
( ), = 1 ÷ , |
то интегральную сумму |
||||||
∆ = ∆ ∙ 0 |
|||||||||||
можно записать в виде: |
= ∑ |
|
|
|
|
|
Пусть λ = |
|
|
- наибольший из |
|
|
|
( )∙∆ . |
|
||||||||
|
|
=1 |
|
|
|
|
1≤ ≤ |
|
|
|
|
диаметров частичных поверхностей - ранг разбиения. |
|
|
|
|
|||||||
Определение 3.14. |
|
|
|
|
|
|
|
|
|
|
|
Число называется пределом интегральных сумм |
при λ → 0, если для > 0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
> 0 такое, что для любого разбиения поверхности с рангом разбиения λ < и при
любом выборе промежуточных точек { |
} |
|
выполняется неравенство: |
||
|
|
=1 |
|
|
|
|
| |
− | < . |
|
||
|
|
|
|
|
|
Запись: = - означает, что при λ → 0 |
этот предел существует, он не |
||||
λ → 0 |
|
|
|
|
|
зависит ни от способа разбиения, ни от выбора промежуточных точек, и равен числу .
Определение 3.15.
|
Конечный предел интегральных сумм |
|
при λ → 0 называется поверхностным |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интегралом 2 рода от вектор-функции ( ) по поверхности . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Обозначение: |
|
|
|
|
|
|
Таким образом, имеем равенство: |
|
|
|
|
|
|
|||||||||||||||||
|
|
( )∙ . |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
( ) ∙ = |
=1 |
( |
) ∙ ∆ |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
λ → 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Существует простая связь между поверхностными интегралами 1 и 2 рода: |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
( ) |
∙ = |
( ∙ 0) |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В левой части этого равенства стоит поверхностный интеграл 2 рода |
|
|
|
|||||||||||||||||||||||||||
|
( )∙ |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
от вектор-функции ( ), а в правой части - поверхностный интеграл 1 рода |
( ∙ 0) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
от функции ( ) = ( )∙ 0( ), значения которой совпадают с проекцией вектора |
на |
||||||||||||||||||||||||||||||
единичный вектор нормали 0 в точке . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Запишем поверхностный интеграл 2 рода в координатной форме. |
|
|
|
|
|
|||||||||||||||||||||||||
|
Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
( ) = (, , )∙ + (, , )∙ + (, , )∙ , |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где , , γ - направляющие углы вектора |
||||||||||||||||
|
0( ) = ∙ + ∙ + γ∙ , |
||||||||||||||||||||||||||||||
нормали 0 |
в точке . Тогда получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
( |
|
) |
|
|
( |
|
( |
, , |
) |
∙ + |
( |
, , |
) |
∙ + |
( |
, , |
) |
|
) |
. |
|
|||||||||
|
|
|
∙ = |
|
|
|
|
|
|
|
∙ γ |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вектор-функция ( ), для которой существует поверхностный интеграл 2 рода, называется интегрируемой по поверхности .
Пример 3.10.
Пусть ( ) ≡ 0 на поверхности . Тогда имеем:
|
|
|
|
|
|
= |
0 = 0 |
|
|||||
0∙ = |
∑=1 |
0∙∆ |
0∙ = 0. |
||||||||||
|
λ → 0 |
|
|
|
|
|
|
|
λ → 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для поверхностных интегралов 2 рода по замкнутой поверхности принято |
|||||||||||||
следующее обозначение: |
|
|
|
( |
|
) |
|
|
|
|
|||
|
|
∙ . |
|
|
|
|
|||||||
Физический смысл поверхностного интеграла 2 рода: |
|||||||||||||
|
|
|
( |
|
) |
|
|
|
|
( |
|
) |
через поверхность . |
|
П = |
|
|
∙ |
- поток вектора |
|
|
||||||
Теорема 3.9 (достаточное условие интегрируемости).
22
Пусть - гладкая ориентированная поверхность, а вектор-функция ( ) - непрерывна на (т.е. непрерывны все ее координатные функции). Тогда вектор-функция( ) интегрируема по поверхности .
Свойства поверхностного интеграла 2 рода.
Пусть вектор-функции ( ) и ( ) - интегрируемы по поверхности . Тогда справедливы следующие свойства.
1. Антисимметричность.
При изменении ориентации на поверхности поверхностный интеграл 2 рода меняет знак:
|
|
|
|
|
+ ( )∙ = − |
− ( )∙ , |
|||
|
|
|
|
|
где + и −- это одна и та же поверхность , но с противоположными ориентациями.
2. Линейность.
а) постоянный множитель можно выносить за знак поверхностного интеграла 2 рода:
|
|
|
|
|
= ; |
( ∙ ( ))∙ = ∙ |
( )∙ , |
||||
б) поверхностный интеграл 2 рода от суммы вектор-функций равен сумме поверхностных интегралов 2 рода от этих вектор-функций:
( |
|
) |
( |
) |
|
( |
) |
( |
) |
( |
|
+ |
|
)∙ = |
|
∙ + |
|
∙ . |
Свойство линейности можно записать в следующем виде:
|
|
|
= 1∙ |
|
|
|
|
1, 2 = . |
(1 ∙ ( ) + 2 |
∙ ( ))∙ |
( )∙ + 2∙ |
( )∙ |
|||||
|
|
|
|
|
|
|
|
|
3. Аддитивность. |
|
|
|
|
|
|
|
|
Если поверхность разбита на две части, то поверхностный интеграл 2 рода по поверхности равен сумме поверхностных интегралов 2 рода по каждой из этих частей:
= 1 2, 1 ∩ 2 = |
|
|
|
|
|
|
|
|
( )∙ = |
( )∙ + |
( )∙ . |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
Доказательство всех этих свойств аналогично доказательству в случае |
|
|
||||||
криволинейных интегралов 2 рода. |
|
|
|
|
|
|
|
|
3.4. Вычисление поверхностного интеграла 2 рода |
|
|
|
|||||
Рассмотрим методы вычисления поверхностного интеграла 2 рода |
|
|
|
|||||
( )∙ . |
||||||||
|
|
|
)}, |
0( ) = { ; ; γ} |
||||
Пусть ( ) = { ( , , ); ( , , ); ( , , |
||||||||
( , , γ − направляющие углы вектора нормали 0 в точке ).
Тогда поверхностный интеграл 2 рода выражается через поверхностные интегралы 1 рода по следующим формулам:
= { ( , , ) ∙ + ( , , ) ∙ + ( , , ) ∙ γ} =
=( , , )∙ + ( , , )∙ + ( , , )∙ γ .
3.4.1. Метод проектирования на все три координатные плоскости
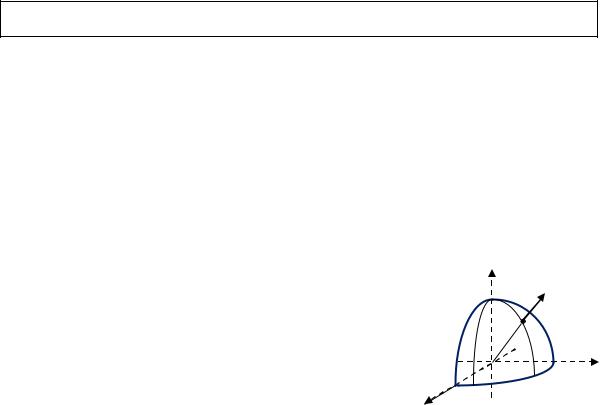
Пусть поверхность взаимно-однозначно проектируется на все три координатные плоскости , , и соответственно: , , - ее проекции на эти плоскости.
При этом поверхность задается следующими уравнениями:
= ( , ), где ( , ) ; = ( , ), где ( , ) ; = ( , ), где ( , ) .
23
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этих случаях вектор нормали к поверхности и его направляющие косинусы |
||||||||||||||||||||||||||||||
(с точностью до знака) вычисляются по формулам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
′ |
′ |
|
| ∙ | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= ( , ) {− |
; − ; 1} γ = ± |
|
|
|
= ± |
|
|
|
= ± |
|
|
|
|
|
|
; |
|
|
|
|||||||||||
|
|
|
|
|
| |∙| | |
|
|
| | |
|
|
|
√1 + (′ )2 + (′ )2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
′ |
|
′ |
|
|
|
| ∙ | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= ( , ) |
{− ; 1; − } = ± |
|
|
|
|
|
|
|
= ± |
|
|
|
|
= ± |
√1 + (′ )2 |
|
; |
|||||||||||||
|
|
|
|
|
|
|
| |∙| | |
|
|
|
| | |
|
|
+ (′)2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
′ |
′ |
|
|
|
| ∙ | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= ( , ) {1; − ; − } = ± |
|
|
|
|
|
|
|
= ± |
|
|
|
|
= ± |
|
|
|
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|
| |∙| | |
|
|
|
| | |
|
|
√1 + (′ )2 + (′ )2 |
||||||||||||||||
|
Применим формулы для поверхностных интегралов 1 рода (см. п. 3.2.3): |
||||||||||||||||||||||||||||||
|
( , , )∙ = ± |
|
|
1 |
|
|
= ± |
( ( , ), , ) ; |
|||||||||||||||||||||||
( ( , ), , )| | |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
( , , )∙ = ± |
|
|
|
1 |
|
= ± |
( , ( , ), ) ; |
|||||||||||||||||||||||
( , ( , ), )| | |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
( , , )∙ γ = ± |
|
|
1 |
|
= ± |
( , , ( , )) . |
||||||||||||||||||||||||
( , , ( , ))|| |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, имеем формулу для вычисления поверхностного интеграла 2 рода через двойные интегралы:
= ± ( ( , ), , ) ± ( , ( , ), ) ± ( , , ( , )) .
Знак перед каждым двойным интегралом должен совпадать со знаком соответствующего косинуса. Например, если - острый угол, то > 0 и знак « + »; если - тупой угол, то < 0 и знак « − ».
Поверхностный интеграл 2 рода может быть записан в следующей форме:
|
|
|
|
(, , ) + (, , ) + (, , ) или: |
|
( )∙ = |
|||||
|
|
|
|
|
(, , ) + (, , ) + (, , ) . |
|
( )∙ = |
||||
В этом случае будут аналогичные формулы:
|
( , , ) = ± |
( ( , ), , ) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( , , ) = ± |
( , ( , ), ) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( , , ) = ± |
( , , ( , )) . |
|
|
|
|
|
||
|
1 |
|
0 |
||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Пример 3.11. |
|
|
|
|
|
|
|
|
|
Вычислить поверхностный интеграл 2 рода |
|
O |
1 |
|
|||||
от вектор-функции |
|
|
|
|
|||||
|
|
|
|
|
|
||||
( ) = ∙ + ∙ + ∙ |
|
|
|
|
|
|
|||
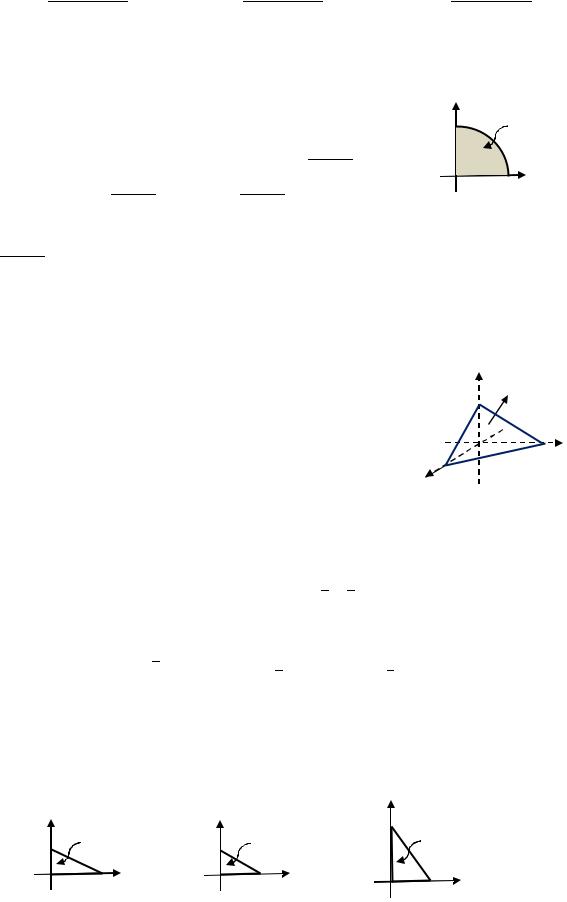
через часть сферы 2 + 2 + 2 = 1, расположенной |
|
|
|
|
|
||||
1 |
|
|
|
|
|||||
в первом октанте в направлении внешней нормали (рис. 3.25). |
|
|
|
|
|
||||
|
|
|
|
|
|
||||
Решение. |
|
|
|
Рис. 3.25. К Примеру 3.11 |
|||||
|
|
|
|
= |
|
|
|
||
|
= ( )∙ = + + |
|
|
|
|||||
= ± ( , )∙ ± ( , )∙ ± ∙( , ) .
Из уравнения сферы: 2 + 2 + 2 = 1 - выразим соответствующие функции:
|
|
|
|
|
|
|
|
|
( , ) = √1 − 2 − 2; |
( , ) = √1 − 2 − 2 |
; |
( , ) = √1 − 2 − 2. |
|||||
Внешняя нормаль образует острые углы со всеми осями координат (рис. 3.25), следовательно, перед интегралами везде ставим знаки « + »:
24
= √1 − 2 − 2∙ + √1 − 2 − 2∙ + ∙√1 − 2 − 2 .
Каждая из проекций , , представляет собой часть круга радиуса 1, лежащую в первой четверти (рис. 3.26). Вычислим первое из этих слагаемых, переходя к
полярным координатам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∙ ] = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
√1 − 2 − 2∙ = [ |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(∫1 2√1 − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= |
′ 2√1 − 2 |
∙ = |
∫ |
2 |
|
) = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
∙∫1 2√1 − 2 |
= ∫1 2√1 − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
= ∫ |
2 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.26. Проекция |
||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
на плоскость |
||||||||||||||||||||||
= [ |
|
= ] = ∫0 |
2 |
2 |
∙ 2 = |
∙∫0 |
2 |
22 = |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
√1 − 2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
1 |
|
|
|
|
|
|
1− 4 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
= |
|
∙∫ |
|
= |
∙( − |
4 ) |2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
2 |
Аналогично получим: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
2 |
|
|
|
|
|
|
8 |
|
|
4 |
|
|
|
0 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
( , )∙ = |
|
|
∙( , ) = |
|
|
= |
|
+ |
|
+ |
|
= |
3 |
. |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
16 |
16 |
16 |
|
16 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Ответ: |
= |
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 3.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
Вычислить = |
− + |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
3 |
|
|||||||||||||
через верхнюю сторону части плоскости |
|
|
|
+ |
|
+ |
|
|
= 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
2 |
|
3 |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
вырезаемой координатными плоскостями (рис. 3.27). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
Учитывая, что вектор 0 |
образует острые углы |
|
|
|
Рис. 3.27. К Примеру 3.12 |
|||||||||||||||||||||||||||||||||||||||||||||||
сосями координат, получаем:
= − + ( , ) =
= − + (1 − 2 − 3) .
Вычислим отдельно каждый из двойных интегралов. Проекции поверхности на координатные плоскости показаны на рисунке 3.28.
1. = ∫03 ∫01− 3 = ∫03 (1 − 3) = ∫03 ( − 13 2) =
= ( |
1 |
2 − |
|
1 |
3) |03 = |
9 |
|
− 3 = |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
9 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
= ∫2 |
∫1− |
|
= ∫2 |
|
1 |
|
|1− |
|
) = |
|
|
|
|
|
||||||||||||||||||||||
2. |
( |
2 |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
0 |
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= ∫2 |
1 |
(1 − |
|
|
)2 = |
|
1 |
∙ |
1 |
|
(1 − |
|
)3∙(−2)|02 |
= − |
1 |
(0 − 1) = |
|
1 |
. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
2 |
|
|
|
2 |
3 |
|
|
|
||||||||||||||||||||||||||||
0 2 |
|
|
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 3.28. Проекции на координатные плоскости
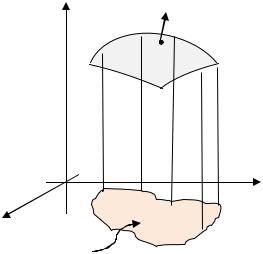
25
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫2 ∫ 3(1− |
|
) (1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
3. |
|
|
|
(1 − |
|
− |
) = |
2 |
− |
) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
= ∫2 |
|
|
|
) |3(1− |
|
) − |
|
1 |
2|3(1− |
|
)) = ∫2 |
|
|
|
)2 − |
3 |
(1 − |
|
|
)2) = |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
((1 − |
|
2 |
2 |
(3 (1 − |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
6 |
2 |
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|
1 |
|
||||||||||||||||||
= |
∫ |
|
|
|
(1 − |
|
|
) = |
|
|
|
|
∙ |
|
|
|
|
(1 − |
|
|
) ∙(−2)| |
0 |
= 1. В результате получим: |
= |
|
|
− |
|
|
|
+ 1 = 2 |
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
2 |
2 |
3 |
6 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Ответ: |
= 2 |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
3.4.2. Метод проектирования на одну координатную плоскость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Пусть поверхность проектируется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
взаимно-однозначно на плоскость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
в область |
|
|
|
|
|
(рис. 3.29). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ( , ) |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
В этом случае поверхность можно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
задать уравнением: = ( , ), а орт 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
нормали к поверхности вычисляется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{− ′ |
;− ′ |
; 1} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 = ± ∙ |
|
|
|
= ± |
|
√1 + |
( ′ )2 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
|
+ |
( ′ )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Тогда поверхностный интеграл 2 рода |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
преобразуется к виду: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= |
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
|
|
|
|
( |
|
) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
∙ = |
|
|
|
|
|
|
|
∙ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
( )∙ 0( )∙| | = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.29. Проекции поверхности на |
|
|
|
|
|||||||||||||||||||||||||||||||||
= ± |
( )∙ ∙ |
|
|
∙| | = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскость |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= ± |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
( )∙ = ± |
|
{ ( , , ); ( , , ); ( , , )}∙{− ; − ; 1} = |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= ± |
|
{− ( , , ( , )) ∙ ′ |
|
− ( , , ( , )) ∙ ′ + ( , , ( , ))} . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знак перед двойным интегралом берется « + », если угол между осью и |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вектором 0 - острый и берется |
|
« − », если угол между осью и вектором 0 - тупой. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Аналогичные формулы для вычисления поверхностных интегралов 2 рода можно |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
получить в случае взаимно-однозначного проектирования поверхности на другие |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
координатные плоскости: |
|
|
|
и |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Таким образом, имеем следующие формулы для вычисления |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
поверхностных интегралов 2 рода: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
= ± |
|
|
|
|
{− ( , , ( , )) ∙ ′ |
− ( , , ( , )) ∙ ′ |
+ ( , , ( , ))} |
, |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
= ± |
|
|
|
|
{− ( , ( , ), ) ∙ ′ |
+ ( , ( , ), ) − ( , ( , ), ) ∙ ′} |
|
, |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
= ± |
|
|
|
|
{ ( ( , ), , ) − ( ( , ), , ) ∙ ′ − ( ( , ), , ) ∙ ′ } |
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 3.13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
Вычислить поверхностный интеграл 2 рода от вектор-функции |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
( ) = |
|
∙ + ∙ |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
по внешней стороне параболоида = 2 |
+ 2, ограниченного плоскостью = 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение.
