
26
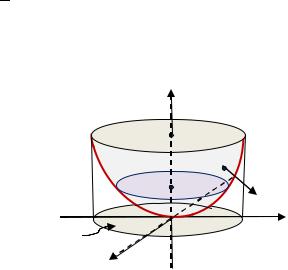
Параболоид проектируется взаимно-однозначно на плоскость в круг с центром в начале координат и радиуса √2 (рис. 3.30). Внешняя нормаль 0 образует тупой угол с осью , поэтому в формуле перед двойным интегралом берем знак « − »:
|
|
|
|
|
|
{− ( , , (, )) ∙ |
′ |
− ( , , (, )) ∙ |
′ |
+ ( , , (, ))} . |
|||||||||||||||||||||||||||||||||||||
( )∙ = − |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Здесь имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
( , , ) = 0, ( , , ) = 2, ( , , ) = ; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
( , ) = 2 + 2, ′ |
= 2, |
′ = 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= − {−0 ∙ 2 − 2 ∙ 2 + 2 + 2} = |
|
|
|
|
|
|
|
|
|
= 2 + 2 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
(23 − 2 − 2) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
= ∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
||||||||||||
|
|
|
|
|
|
= [ = ∙ ] = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= ′ |
(23 3 − 2)∙ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.30. |
К Примеру 3.13 |
|||||||||||
= ∫02 (∫0√2(24 3 − 3) ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
= ∫ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
(3 ( |
2 |
5 |
|√2) − |
1 |
4 |
|√2) = |
( |
8√2 |
|
3 − 1) = |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
5 |
|
0 |
|
|
4 |
|
|
0 |
|
|
0 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ 2 (1 − 2) ( ) − 2 = |
|
|
|
|||||||||||||||||||||||||||||||
= |
8√2 |
|
∫ 2 3 − 2 = − |
|
8√2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
5 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
5 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
3) |2 − 2 = − |
|
|
|
|
|
|
|
|
) |2 |
|
|
|
|
|
||||||||||||||||||||||||||||
= − |
8√ |
2 |
( − |
1 |
|
8√2 |
( |
2 |
− |
2 |
− 2 = 0 − 2 = −2. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
5 |
3 |
|
|
0 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
3 |
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|||||||||||||||||
Ответ: = −2.
В конкретных примерах на вычисление поверхностных интегралов 2 рода можно применять оба метода: метод проектирования на все три координатные плоскости и метод проектирования на одну координатную плоскость.
|
|
В Примере 3.12 вычислен поверхностный интеграл 2 рода от вектор-функции |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
+ |
|
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
через поверхность : { |
|
2 |
3 |
1 |
|
|
|
|
(рис. 3.27) методом |
|
||||||||||||||||||||||||||||||||||||||
( ) = ∙ − ∙ + ∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≥ 0, ≥ 0, ≥ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
проектирования на все три координатные плоскости. Так как поверхность взаимно- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
однозначно проектируется на плоскость , то можно здесь применить и метод |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
проектирования на одну координатную плоскость. Покажем это. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{− ( , , (, )) ∙ |
′ |
− ( , , (, )) ∙ |
′ |
+ ( , , (, ))} |
||||||||||||||||||||||||||||||||||||||||||||
|
( )∙ = |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Здесь имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
( , , ) = , ( , , ) = − , ( , , ) = , |
( , ) = 1 − |
|
− |
|
, |
|
′ |
= − |
1 |
, |
′ |
= − |
1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= |
|
{ ∙ |
1 |
− ( , ) ∙ |
1 |
+ ( , )} = |
{ |
1 |
− |
1 |
(1 − |
|
|
− |
|
) + 1 − |
|
− |
|
} = |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
3 |
2 |
|
|
|
3 |
|
2 |
|
3 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
= |
|
{ |
1 |
|
− |
1 |
+ |
1 |
|
+ |
1 |
+ 1 − |
1 |
− |
1 |
} = |
{ |
2 |
|
− |
1 |
+ |
5 |
|
} , |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
3 6 |
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
3 3 |
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
: { |
|
|
|
|
0 ≤ ≤ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 3.28). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0 ≤ ≤ 3 (1 − |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вычисляя двойной интеграл через повторный интеграл, получим:
= ∫2 |
∫ 3(1− |
|
) |
|
2 |
|
1 |
|
5 |
) = ∫2 |
|
2 |
|
1 |
) |3(1− |
|
) |
|
5 |
2|3(1− |
|
)) = |
||
2 |
( |
− |
+ |
(( |
− |
2 |
+ |
2 |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
3 |
18 |
|
3 |
36 |
|||||||||||||||||||
0 |
0 |
|
|
3 |
|
|
0 |
3 |
|
0 |
|
|
|
0 |
|
|
||||||||
27
= ∫02 ((2 − ) (1 − 2) + 54 (1 − 2)2) = ∫02 (2 − 2 + 12 2 + 54 (1 − 2)2) =
= (2 − 2 + 16 3) |20 + 125 ∙(1 − 2)3∙(−2)|20 = 43 + 56 = 136 = 2 16.
Приходим к такому же результату, что и в Примере 3.12.
3.4.3.Приложения поверхностных интегралов 2 рода
1.Основным приложением поверхностных интегралов 2 рода является вычисление
потока вектора через заданную поверхность :
П = |
( |
) |
( |
) |
∙ 0 |
( |
) |
. |
|
∙ = |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
В этих приложениях часто возникают задачи на вычисление потока через плоские области. Рассмотрим этот частный случай, когда поверхность является плоской областью.
Поток вектора через плоскую область. |
|
|
|
||
|
|
|
|||
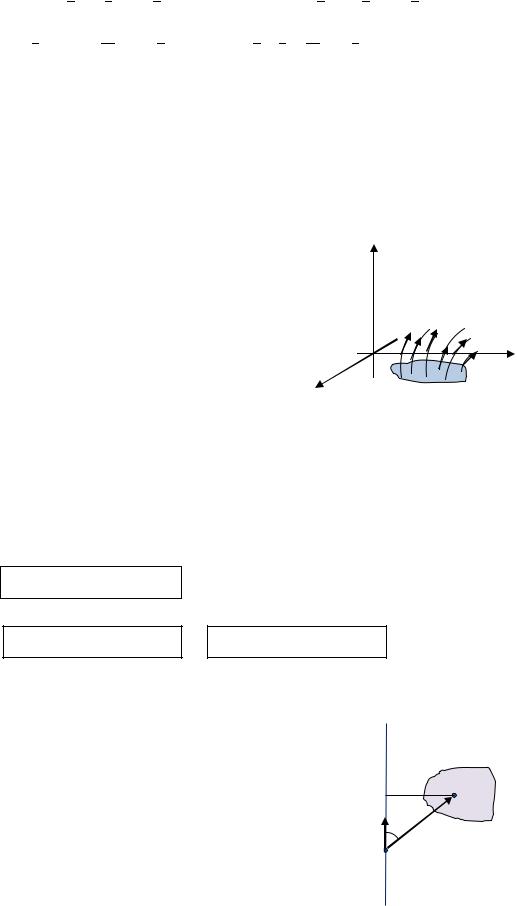
Пусть поверхность – это область , лежащая |
|
|
|||
в плоскости (рис. 3.31): |
|
|
|
||
|
|
|
|
|
( ) |
|
= 0 |
( , , ) |
|
O |
|
|
|
|
|||
: {( , ) |
и ( ) = (( , , )). |
|
|
|
|
|
|
( , , ) |
|
|
|
В этом случае имеем: |
|
|
|||
|
Рис. 3.31. |
Поток вектора |
|||
( , ) = 0, ′ |
= 0, ′ = 0, |
|
|||
|
|
|
|||
|
|
|
|
через плоскую область |
|
а формула для вычисления поверхностного интеграла |
|
||||
|
|
|
|||
2 рода принимает вид: |
|
|
|
||
П = ± |
{− ( , , ( , )) ∙ ′ − ( , , ( , )) ∙ ′ |
+ ( , , ( , ))} = |
|||
|
|
|
|
|
|
|
|
|
|
|
|
= ± ( , , ( , )) = ± ( , , 0) .
Таким образом, в случае потока вектора через плоскую область имеем
формулу: П = ± ( , , 0) . Аналогичные формулы получаются в случае
расположения области в координатных плоскостях и :
П = ± ( , 0, ) и П = ± (0, , ) .
В этих формулах берется знак « + », если поток вычисляется в направлении, совпадающем с направлением соответствующей оси координат, и берется знак « − » в
противном случае. |
|
|
|
|
|
|
Рассмотрим следующую задачу. |
|
|
|
|||
Задача (о вычислении магнитного потока). |
|
|
||||
Рассматривается бесконечно длинный тонкий |
|
|
||||
прямой провод с током , который создает магнитное поле, |
|
|
||||
|
|
|||||
характеризуемое в каждой точке пространства вектором |
|
|||||
|
|
|||||
|
|
|
|
|||
магнитной индукции . |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|||
Вектор магнитной индукции |
|
|
|
|||
в произвольной точке выражается |
|
|
|
|||
|
0 |
|
|
|
|
|
векторным произведением: = |
2 ∙ 2∙( × ), |
Рис. 3.32. К определению |
||||
|
|
|
|
вектора магнитной индукции |
||
28
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
- расстояние |
|
|
|
|
|
|
|
|||||||
- радиус-вектор точки , |
|
|
|
|
|
|
|
|||||||||||||||||||||
от точки до проводника (рис. 3.32), 0 - магнитная постоянная. |
|
|
|
|
||||||||||||||||||||||||
|
В одной плоскости с проводником расположена не пересекающая проводник |
|||||||||||||||||||||||||||
плоская рамка заданной формы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Требуется найти величину (модуль) магнитного потока Ф сквозь данную рамку: |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф = |
( |
|
) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ . |
|
|
|
|
|
|||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введем систему координат так, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
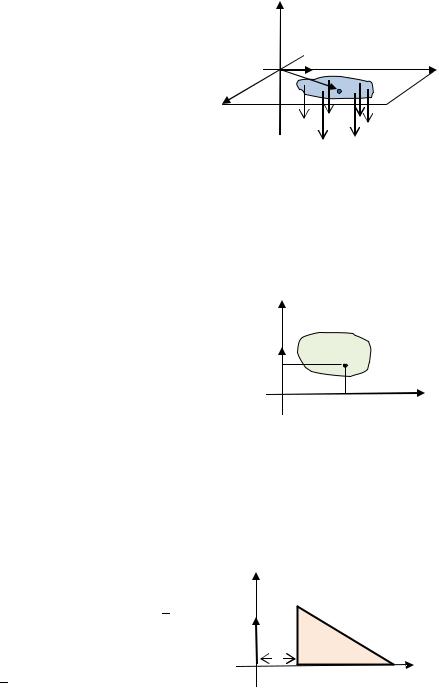
чтобы проводник и рамка лежали в плоскости |
|
|
|
|
O |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
(рис. 3.33), при этом ось направим |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вдоль проводника. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из определения магнитной индукции |
|
|
|
|
|
|
|
|
|
( ) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
следует, что вектор |
|
перпендикулярен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
Рис. 3.33. Введение системы |
||||||||||||||||||
плоскости , т.е. направлен по оси |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
декартовых координат |
|||||||||||||||||||||
(в отрицательном направлении): |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0∙ |
|
0∙ |
|
|
|
||
|
( ) |
= −| |∙ = − |
2 ∙ 2∙| |∙| |∙ ∙ = − |
2 ∙ 2∙ ∙ = − |
2 ∙ ∙ |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0∙ |
|
|
|
|
|
|
|
|
|
|
|
|||
|
( ) |
= − ∙ = − ∙ , |
где |
= |
2 = . |
|
|
|
|
|
|
|||||||||||||||||
|
По условию задачи требуется найти величину (модуль) магнитного потока Ф, |
|||||||||||||||||||||||||||
поэтому направление вектора нормали 0( ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
выберем так, чтобы поток был положителен, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
т.е. |
|
|
Тогда получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0( ) = − . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||
= ( )∙ = |
( )∙ 0( ) = |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Таким образом, магнитный поток сквозь рамку , |
|
|
|
|
|
||||||||||||||||||||||
расположенную в плоскости (рис. 3.34), |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
Рис. 3.34. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
вычисляется по формуле: |
|
Ф |
= |
0∙ |
∙ |
1 |
|
. |
|
|
||||||||||||||||||
|
|
|
К вычислению |
|||||||||||||||||||||||||
|
2 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
магнитного потока |
||||||
Пример 3.14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Найти магнитный поток сквозь плоскую рамку, имеющую форму прямоугольного |
|||||||||||||||||||||||||||
треугольника со сторонами, показанными на рисунке 3.35. |
|
|
|
|
||||||||||||||||||||||||
Решение.
Применим полученную выше формулу для вычисления магнитного потока: Ф = ∙ 1 ,
где = , а область задается неравенствами:
≤ ≤ + {0 ≤ ≤ ( + − ).
Вычисляя двойной интеграл с помощью повторного интеграла, получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.35. К Примеру 3.14
|
|
|
+ |
|
|
(+ − ) 1 |
|
|
|
+ 1 |
|
|
(+ − ) |
|
+ |
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
( |
( + − )) |
|
|||||||||||||||||
Ф = ∙∫ |
|
|
∫ |
|
|
|
|
= ∙∫ |
|
|
∫ |
= ∙∫ |
|
|
|
|
= = |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||
∙∫ + |
( |
|
|
( + ) |
1 |
− |
|
) = ∙( |
|
( + ) ∙ | + − ) = ∙((1 + |
|
|
) ∙ (1 + |
|
) − 1)∙ . |
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
29
Ответ: Ф = |
|
0∙ |
∙((1 + |
|
) ∙ (1 + |
|
) − 1)∙ . |
|
|
|||||
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
||||||
2. Одно из приложений поверхностных интегралов 2 рода связано с вычислением |
||||||||||||||
объема тела Ω, ограниченного замкнутой поверхностью : |
|
|||||||||||||
(Ω |
) |
= ; |
) |
|
) |
; |
||||||||
|
|
(Ω = ; |
(Ω = |
|||||||||||
|
|
|
|
(Ω |
) |
1 |
( + + ) |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
= 3 |
|
|||||||||
|
|
|
|
|
|
|||||||||
(во всех случаях интеграл берется по внешней стороне замкнутой поверхности).
Пример 3.15.
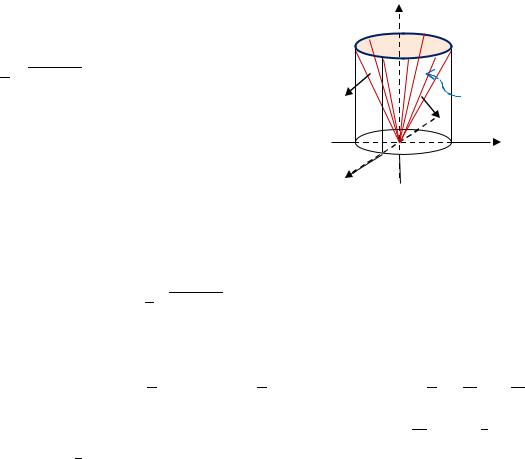
Вычислить с помощью поверхностного интеграла 2 рода объем прямого кругового
конуса высотой и радиусом основания . |
|
Решение. |
|
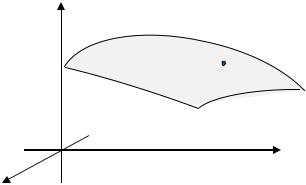
Конус Ω высотой и радиусом основания задается неравенствами (рис. 3.36):
∙√2 + 2 ≤ ≤ .
Полная поверхность конуса состоит из основания 0и боковой поверхности бок:
= 0 бок.
Применим формулу для объема тела:
(Ω) = = 0 + бок .
Вычислим интеграл по основанию конуса:

0 |
|
|
|
|
|
|
= |
∙ √2 + 2 |
|||
|
|||||
|
0 |
|
|
|
|
O
Рис. 3.36. К Примеру 3.15
0 = 0 = ∙ 0 = ∙(0) = ∙ 2 = 2 .
Вычислим интеграл по боковой поверхности конуса (рис. 3.36):
бок = − ∙√2 + 2 =
перед интегралом берем знак « − », так как вектор нормали 0 в каждой точке [образует тупой угол с осью ; − проекция бок на плоскость − круг радиуса ]
= ∙
=[ = ∙ ] = − ′ ∙ 2 = − ∫02 (∫0 2 ) = − ∙2 3 = − 2 2 .= 3 3
Складывая найденные величины, получим: (Ω) = 2 − 23 2 = 13 2 .
Ответ: конуса = 13 2 .
Глава 4. Элементы теории поля
Теория поля – раздел математики, физики и механики, в котором изучаются скалярные, векторные и иные поля. Полем называется любая область в пространстве или на плоскости, в которой задана некоторая (скалярная или векторная) величина.
Примеры скалярных полей: поле температуры воздуха, поле атмосферного давления, поле электрического потенциала и т.д. Примеры векторных полей: силовое поле, поле скоростей в потоке движения, поле электрического тока, магнитное поле и т.д.
Инструментом изучения таких полей служат кратные, криволинейные и поверхностные интегралы, рассмотренные в предыдущих главах.
4.1. Скалярное поле
Определение 4.1.
Пусть в некоторой области (пространства или плоскости) задана функция = ( ), . Тогда пара ( ; ) или запись вида: { = ( ), } - называется
скалярным полем.
Область при этом может быть ограниченной или неограниченной областью, в частности может и совпадать со всем пространством 3 или плоскостью 2.
Если 3, то = ( , , ) – функция 3-х переменных. Если 2, то = ( , ) - функция 2-х переменных, и в этом случае имеем плоское скалярное поле.
4.1.1. Линии и поверхности уровня
Наглядным представлением скалярного поля служат такие его геометрические характеристики как линии и поверхности уровня.
Определение 4.2.
Поверхностью уровня скалярного поля { = ( ), 3} называется множество всех точек области , в которых значения функции постоянны и равны :
|
|
= { : ( ) = }, |
= . |
|||||
|
|
|
|
|
|
|
|
|
Например: изотермы – это поверхности одинаковых температур, изобары – это |
||||||||
поверхности одинаковых атмосферных давлений. |
|
|||||||
Поверхность уровня данного |
|
|
||||||
|
|
|
|
|
|
|
( , , ) = |
|
скалярного поля при фиксированном |
||||||||
|
|
|||||||
значении определяется уравнением |
|
|
||||||
(рис. 4.1): |
|
|
|
|
|
|
||
|
( , , ) = |
. |
|
|
||||
Придавая константе в этом |
|
|
||||||
уравнении различные значения, получим |
|
|
||||||
целое семейство поверхностей уровня: |
O |
|||||||
|
|
|||||||
|
{ , |
}. |
|
|
|
|||
|
|
|
|
|
||||
Заметим, что поверхности уровня, |
|
|
||||||
соответствующие различным значениям , |
Рис. 4.1. Поверхность уровня |
|||||||
не пересекаются: |
|
|
|
|
|
скалярного поля |
||
|
≠ |
|
∩ |
|
= . |
|
|
|
|
|
|
|
|
|
|
||
Пример 4.1. |
|
|
|
|
|
|
||
Описать поверхности уровня следующих скалярных полей: |
||||||||
а) = + + ; |
|
б) = 2 + 2 + 2; |
в) = 2 + 2 − 2. |
|||||
2
Решение.
а) { ( , , ) 3: + + = , } - это семейство параллельных плоскостей в пространстве с вектором нормали 0 {1; 1; 1};
б) { ( , , ) 3: 2 + 2 + 2 = , ≥ 0} - это семейство концентрических сфер с центром в начале координат (при > 0) и точка (0; 0; 0) (при = 0);
в) { ( , , ) 3: 2 + 2 − 2 = , } - это семейство однополостных (при> 0) или двуполостных (при < 0) гиперболоидов с осью ; при = 0 поверхностью уровня будет круговой конус.
Ответ: а) семейство параллельных плоскостей; б) семейство концентрических сфер; в) семейство гиперболоидов и круговой конус.
Определение 4.3.
Линией уровня плоского скалярного поля { = ( ), 2} называется множество всех точек области , в которых значения функции постоянны и равны :
= { : ( ) = }, = .
Например: горизонтали при изображении рельефа местности на топографической карте – это изолинии одинаковых высот, изоклины дифференциального уравнения - это линии, в точках пересечения с которыми интегральные кривые наклонены к оси абсцисс под одним и тем же углом.
|
Линия уровня |
плоского скалярного |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
поля при фиксированном значении определяется |
(, ) = |
|||||||||
|
||||||||||
уравнением: |
|
|
|
|
|
|
|
(, ) = |
||
|
( , ) = . |
|
|
|
|
|
||||
|
Придавая константе в этом уравнении |
|
|
(, ) = |
||||||
различные значения, получим целое |
|
|
|
|
||||||
семейство линий уровня (рис. 4.2): |
|
|
|
|
||||||
|
{ , |
}. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
Заметим, что линии уровня, |
|
|
|
|
|||||
соответствующие различным значениям , |
|
Рис. 4.2. Линии уровня |
||||||||
не пересекаются: |
|
|
|
|
|
|
скалярного поля |
|||
|
≠ |
|
|
∩ |
= . |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
Пример 4.2. |
|
|
|
|
|
|
|
|
||
|
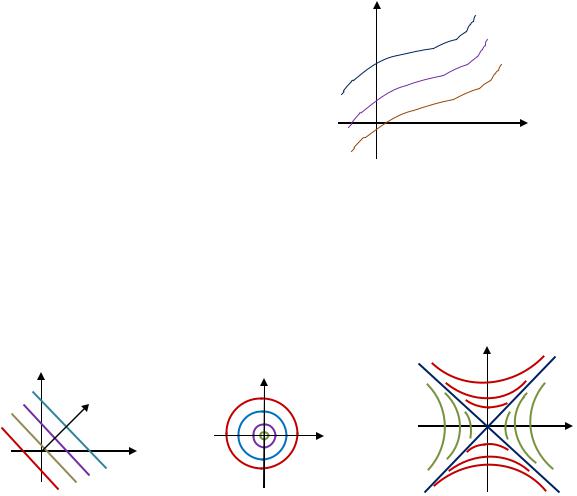
Построить линии уровня следующих скалярных полей: |
|
||||||||
|
а) = + ; |
б) = 2 + 2; |
в) = 2 − 2. |
|
||||||
|
|
|
|
|
|
|
|
в) |
|
|
а) |
|
|
|
|
б) |
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.3. Линии уровня скалярных полей из Примера 4.2 |
|
||||||||

3
Решение.
а) { ( , ) 2: + = , } – это семейство параллельных прямых с
вектором нормали {1; 1}. (рис. 4.3-а); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
б) { ( , ) 2: 2 + 2 |
= , ≥ 0} - это семейство концентрических |
|||||||||||||||||||
окружностей с центром в начале координат (при > 0) и точка (0; 0) (при |
= 0) |
|||||||||||||||||||
(рис. 4.3-б); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) { ( , ) 2: 2 − 2 |
= , } – это семейство гипербол (при |
≠ 0) и |
||||||||||||||||||
пара прямых (при = 0) (рис. 4.3-в). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: Линии уровня изображены на рисунке 4.3. |
|
|
|
|
|
|||||||||||||||
4.1.2. Производная по направлению |
|
|
|
|||||||||||||||||
Для характеристики скорости изменения скалярного поля в различных |
|
|||||||||||||||||||
направлениях вводится понятие производной по направлению. |
|
|
|
|||||||||||||||||
Рассмотрим скалярное поле = ( ), . |
|
|
|
|
|
|||||||||||||||
Пусть 0 - фиксированная точка и - ненулевой вектор. |
|
|
||||||||||||||||||
Проведем луч из точки 0 в направлении вектора |
|
|
0 |
|
||||||||||||||||
(рис. 4.4). Пусть - произвольная точка на этом луче. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||
Рассмотрим приращение ∆ (0) скалярного поля |
|
|
|
|||||||||||||||||
в точке 0 в направлении вектора : |
|
|
|
|
|
|
|
|
|
Рис. 4.4. Луч в |
||||||||||
∆ (0) = ( ) − (0), где |
|
|
|
направлении вектора |
||||||||||||||||
0 |
. |
|
|
|||||||||||||||||
Устремим точку к точке 0 вдоль этого луча. |
|
|
|
|
|
|||||||||||||||
Определение 4.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если существует предел отношения |
∆ (0) |
|
|
|
|
|
|
|
||||||||||||
|
|
|
при → 0 и 0 , то он |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
| 0 | |
|
|
|
|
|
|
||||
называется производной |
|
( ) скалярного поля в точке |
по направлению вектора . |
|||||||||||||||||
|
||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Итак, по определению имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
∆ |
|
(0) |
|
|
|
|
( )− ( ) |
|
|||||
|
|
( ) = |
|
|
|
|
|
= |
|
|
|
0 |
. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 |
|
→ 0 |
|
|
|
→ 0 |
|
|
|
|
|||||||
|
|
|
|
|
| 0 | |
|
| 0 | |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
||
Производная по направлению характеризует скорость изменения скалярного поля в данной точке по заданному направлению. При этом если (0) > 0, то функция ( ) в
направлении возрастает, а если (0) < 0, то ( ) в этом направлении убывает.
Теорема 4.1.
Пусть функция = ( , , ) имеет непрерывные частные производные ′ |
, ′ |
, ′ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
в окрестности точки 0. Тогда в точке 0 |
для любого ненулевого вектора существует |
||||||||||
производная по направлению , которая выражается формулой: |
|
|
|||||||||
|
|
( ) |
= ′ |
( )∙ + ′ |
( )∙ + ′ |
( )∙ γ, |
|
|
|||
|
|
|
|
||||||||
|
|
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где , , γ - направляющие углы вектора . |
|
|
|
|
|
||||||
Доказательство. |
|
|
|
|
|
|
|
|
|
||
Пусть 0(0, 0, 0), (0 + ∆ , 0 |
+ ∆ , 0 |
|
|
|
|
||||||
+ ∆ ); тогда 0 {∆ , ∆ , ∆ } . |
|||||||||||
Из дифференцируемости функции = ( , , ) в точке 0 следует, что ее приращение ∆ (0) в этой точке может быть записано в виде:
∆ ( ) = ′ |
( )∙∆ + ′ |
( )∙∆ + ′ |
( )∙∆ + |
∙∆ + |
∙∆ + ∙∆, |
|||||
|
0 |
|
0 |
|
0 |
|
0 |
1 |
2 |
3 |
4
где 1, 2, 3 → 0 при ∆, ∆, ∆ → 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Введем обозначение: λ = | 0 |; учитывая, что |
0 {∆ ; ∆ ; ∆ } , получим: |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
∆ = λ∙ , |
∆ = λ∙ , |
∆ = λ∙ γ. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Тогда имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
∆ ( 0) |
= ′ |
( ) + ′ |
( ) + ′( ) γ + + + γ. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
λ |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если → 0, то λ → 0 и ∆, ∆, ∆ → 0, следовательно, и |
1, 2, 3 → 0. |
|
|
||||||||||||||||||||||||||||||||||||||||||
Переходя к пределу при → 0, получим нужную формулу. Теорема доказана. |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
В случае плоского скалярного поля = ( , ) имеем формулу: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( ) = ′ ( )∙ + ′ |
( )∙ , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где – угол между вектором |
|
и осью абсцисс. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Пример 4.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Найти производную скалярного поля = в точке 0(1; 2; 3) в направлении |
|||||||||||||||||||||||||||||||||||||||||||||
вектора {1; −2; 2}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Здесь имеем: ′ |
= , ′ = , ′ = ; ′ ( ) = 6, ′ ( ) = 3, |
′( ) = 2. |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Найдем направляющие косинусы вектора : |
| | = √1 + 4 + 4 = 3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
= |
1 |
, = − |
2 |
, γ = |
2 |
. Следовательно: |
|
(0) = 6∙ |
1 |
+ 3∙(− |
2 |
) + 2∙ |
2 |
|
= |
4 |
= 1 |
1 |
. |
|||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
3 |
3 |
3 |
3 |
||||||||||||||||||
Ответ: |
|
|
|
|
(0) = 1 |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Следствие 4.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Пусть |
|
|
- орты осей координат , , . |
Тогда производные по |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
, , |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
направлениям этих ортов совпадают с частными производными по переменным , , : |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
, |
|
= |
|
, |
|
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Замечание 4.1.
Из Следствия 4.1 получаем, что частные производные по переменным , , являются частным случаем производных по направлению, если в качестве направлений взять оси координат. Значит, понятие производной по направлению - это обобщение введенного ранее понятия частных производных.
Понятие производной по направлению тесно связано с понятием градиента
(см. п. 3.1.4).
4.1.3. Градиент скалярного поля
Определение 4.5. |
|
|
|
|
|
|
|
|
|
|
|
|
Градиентом скалярного поля = ( , , ) в точке 0 |
называется вектор |
|||||||||||
|
|
|
′ |
′ |
|
′ |
( )}. |
|
|
|
||
|
|
{ |
( ), |
( ), |
|
|
|
|||||
|
|
|
|
0 |
|
0 |
0 |
|
|
|
|
|
Для градиента приняты обозначения: |
|
|
|
|
|
|
|
|||||
( 0) или |
( 0): |
|
||||||||||
|
|
|
|
|
′ |
( )∙ + |
′ |
|
′ |
|
|
|
= ( ) = ( ) = |
|
( )∙ + |
( )∙ . |
|||||||||
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
Пример 4.4. |
|
|
|
|
|
|
|
|
|
|
|
|
Найти |
|
= | |, |
{ , , } - радиус-вектор точки. |
|
|
|||||||
, где |
|
|
||||||||||
Решение.
|
|
|
|
|
|
|
|
|
|
|
= |
|
; |
|||||||
= |
| | = √2 + 2 + 2 |
′ = |
||||||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√2+ 2+ 2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
{ ; ; } = |
|
|
|
|
|
|
|||||
{ |
|
|
, |
|
, |
|
} = |
|
|
|
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
5 |
′ = |
|
|
= |
|
; ′ = |
|
|
= |
|
|
|
|
|
|
|
|
|||||
|
√2+ 2+ 2 |
|
|
|
√2+ 2+ 2 |
|
|
|
||
|
|
|
|
|
||||||
Ответ: = .
Из формулы для производной по направлению получаем следующее утверждение.
Следствие 4.2.
Производная скалярного поля в точке 0 по направлению вектора равна скалярному произведению вектора градиента на единичный вектор этого направления:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) = (0) |
∙ 0 |
, где |
0 |
|
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
|
||||
Свойства градиента. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1. |
Градиент направлен по нормали к поверхности (линии) уровня. |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
Действительно, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
: ( , , ) = – поверхность уровня, проходящая |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
через точку 0 (рис. 4.5), то согласно п. 3.1.4, имеем: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
′ |
( ), |
′ |
|
|
|
′ |
( )} - вектор нормали |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
{ |
|
( ), |
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
к поверхности , следовательно: |
|
|
|
|
|
) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2. Градиент направлен в сторону |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
наибольшего возрастания скалярного поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
в данной точке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.5. Градиент как |
|||||||||
|
|
|
Это следует из равенства: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нормаль к поверхности уровня |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
(0) = (0)∙ 0 |
= |(0)|∙ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где - угол между градиентом и направлением вектора |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
(рис. 4.6). Максимальное значение это выражение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
принимает в случае, когда |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
т.е. когда (0) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
3. Модуль градиента равен наибольшей скорости |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||||||||||
возрастания скалярного поля в данной точке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
Действительно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.6. Угол между |
|||||
|
|
(0) = {|(0)| ∙ } = |(0)|. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
градиентом и вектором |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Итак, имеем: |
|(0)| = |
|
|
(0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
′ |
|
2 |
|
|
′ |
|
2 |
|
′ 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Заметим, что |(0)| = |
|
|
( ) |
|
+ ( ) |
|
+ ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Пример 4.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Найти величину и направление наибольшего возрастания скалярного поля |
|||||||||||||||||||||||||||||||||||||
= + + в точке 0 (1; 1; 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Здесь имеем: ′ |
= + , ′ |
= + , ′ |
= + ; ′ |
( ) = ′ |
( ) |
= ′ |
( ) = 2; |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
0 |
|
|
|
|
|
|
2} = 2∙{1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(0) = {2; 2; |
1; 1} |(0)| = √12 = 2√3. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Ответ: 2√3 – величина, а {1; 1; 1} - направление наибольшего возрастания.
Правила вычисления градиента.
6
|
|
|
|
|
||
Используем, как и выше, обозначение градиента: = |
|
∙ + |
|
∙ + |
|
∙ . |
Запись такого вида в дальнейшем будем называть оператором «набла» или «оператором Гамильтона». Термин «оператор» означает отображение, функцию или функционал. Оператор Гамильтона можно символически записать в виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
∙ + ∙ + ∙ . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда = ∙ |
- произведение вектора на скалярную (числовую) величину . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Этот оператор преобразует скалярную величину в векторную величину . |
||||||||||||||||||||||||||||||||
Отметим следующие правила действий с оператором |
|
|
|
|
|
|
||||||||||||||||||||||||||
. |
|
|
|
|
|
|||||||||||||||||||||||||||
(1) |
|
|
, |
|
где = . |
|
|
|
(2) |
|
|
|
|
|
|
|
|
|||||||||||||||
= 0 |
|
|
|
|
= , |
= , |
= . |
|||||||||||||||||||||||||
(3) |
|
|
|
|
|
|
|
|
|
|
где = . |
(4) |
|
|
|
|
|
|
|
|
|
|||||||||||
( ∙ ) |
= ∙ , |
( + ) = + . |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ − ∙ |
|
|
|
|||||||||||
(5) |
( ∙ ) |
= ∙ + ∙ . |
|
|
|
(6) |
( |
|
) = |
|
|
. |
|
|
||||||||||||||||||
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||
(7) |
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8) |
|
|
|
′ |
|
′ |
|
|
|||
( ) = |
( )∙ . |
|
|
|
|
|
|
|
( , ) = |
∙ + ∙ . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 4.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из правил (3) и (4) следует, что оператор - это линейный оператор. |
|
|
||||||||||||||||||||||||||||||
Градиент центрального скалярного поля. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Определение 4.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Скалярное поле вида: = ( ), |
где = | | = | { , , }| = √2 + 2 |
+ 2, |
||||||||||||||||||||||||||||||
а { , , } – это радиус-вектор точки, называется центральным скалярным полем. |
||||||||||||||||||||||||||||||||
Пример 4.6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислить градиент центрального скалярного поля = ( ). |
|
|
|
|||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно правилу (7) |
и Примеру 4.4 имеем: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
′ |
|
|
|
|
|
|
|
|
′ |
( )∙ |
|
|
|
′ |
( )∙ 0 |
, где 0 |
- орт вектора ( 0 |
и | 0| = 1). |
||||||||||||
( ) = |
( )∙ = |
|
= |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
′ |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: ( ) = |
|
( )∙ |
|
= |
( )∙ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4.2. Векторное поле
Определение 4.7.
Пусть в некоторой области (пространства или плоскости) задана вектор-функция= ( ), . Тогда пара (; ) или запись вида: { = ( ), } - называется
векторным полем.
Область при этом может быть ограниченной или неограниченной областью, в частности может и совпадать со всем пространством 3 или плоскостью 2.
Если 3, то ( ) = ( , , )∙ + ( , , )∙ + ( , , )∙ - вектор-функция
3-х переменных.
Если 2, то ( ) = ( , )∙ + ( , )∙ + ( , )∙ – вектор-функция 2-х
переменных; если при этом ( , ) ≡ 0, то ( ) = ( , )∙ + ( , )∙ ; в этом случае имеем плоское векторное поле.
4.2.1. Примеры плоских векторных полей
Примером плоского векторного поля является поле линейных скоростей материальной точки , вращающейся с постоянной угловой скоростью вокруг неподвижной оси (рис. 4.7).
