Все лекции

Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

( ) ∆ ( )∙∆ = 0,

Следовательно, имеем:

.pdf

Скачиваний:

Добавлен:

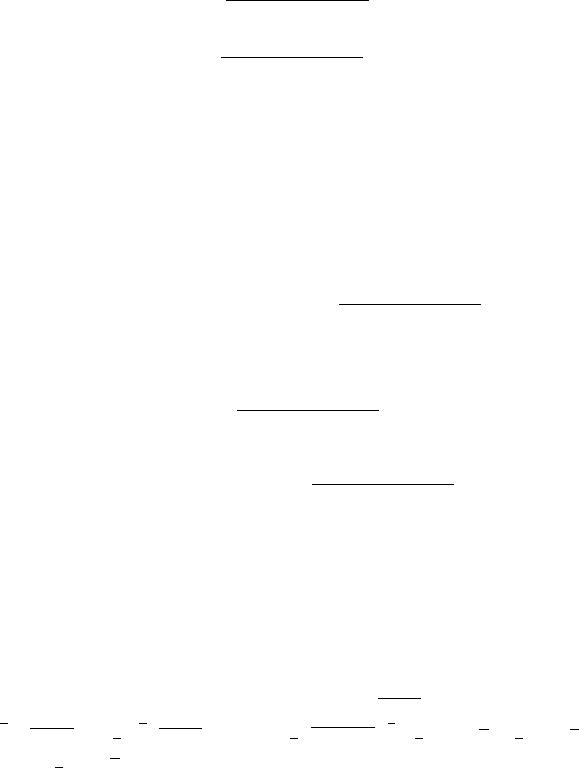
05.06.2021

Размер:

10.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 135 6 7 8 9 10 11 12 13 > Следующая >>>

2.2.2. Вычисление интеграла вдоль пространственной кривой

Рассмотрим гладкую кривую , заданную параметрическими уравнениями:

= ( )

{ = ( ), [ ; ], где ( ), ( ), ( ) - непрерывно-дифференцируемые функции.

= ( )

Для дальнейших выкладок нам потребуется формула для длины кривой. Как известно (см. [4], . ), длина кривой вычисляется по формуле:


		\| \| = ∫ √( ′)2 + ( ′)2 + ( ′)2			.
			̆				- имеем:
Соответственно, для длины дуги = \| \|, где ( ( ), ( ), ( ))							- имеем:
	= ( ) = ∫ √( ′)2 + ( ′)2 + ( ′)2			,		≤ ≤ .
При этом производная функции ( ) равна:

′( ) = √( ′( ))2 + ( ′( ))2 + ( ′( ))2 > 0			[ ; ], что обеспечивает строгое

возрастание функции ( ).

Теорема 2.5.

Пусть - гладкая кривая - задана параметрическими уравнениями:

= ( )

{ = ( ), [ ; ]; пусть функция ( , , ) непрерывна на кривой .

= ( )

Тогда справедлива формула:

∫

( , , ) = ∫ ( ( ), ( ), ( )) ∙ √( ′)2 + ( ′)2 + ( ′)2

Доказательство.
В пункте 2.2.1 получена формула: ∫	( , , ) = ∫0\| \| ( ( ), ( ), ( )) .

Сделаем замену переменной в этом определенном интеграле:

= ( ) = ′( ) = √( ′)2 + ( ′)2 + ( ′)2 [ ( ) = ( ( )) = ( ), ( ) = ( ( )) = ( ), ( ) = ( ( )) = ( )]

0 ≤ ≤ | | ≤ ≤

∫0| | ( ( ), ( ), ( )) = ∫ ( ( ), ( ), ( ))√( ′)2 + ( ′)2 + ( ′)2 .

Теорема доказана.

Пример 2.2.

Вычислить криволинейный интеграл 1 рода = ∫ , где - коническая

			= ∙
винтовая линия (винтовая линия на конусе):			{ = ∙ , [0; √2].
			=
Решение.
	= ∙ ,		= ∙ , =
∫ = [	′( ) = − ∙ ,	′( ) = + ∙ ,		′( ) = 1
∫ = [				] =

= √( ′)2 + ( ′)2 + ( ′)2 = √2 + 2

= ∫0√2 ∙√2 + 2 = 12 ∫0√2 √2 + 2 (2 + 2) = 13 √(2 + 2)3|√02 = 13 (8 − 2√2) = 23 (4 − √2). Ответ: = 23 (4 − √2).

2.2.3. Вычисление интеграла вдоль плоской кривой

= ( )

Вслучае плоской кривой , заданной параметрическими уравнениями: { = ( ),

[ ; ] - имеем следующую формулу для вычисления криволинейного интеграла 1 рода:

∫ ( , ) = ∫ ( ( ), ( ))∙√( ′)2 + ( ′)2 .

Если кривая задана явным уравнением: = ( ), [ ; ] - то формула принимает вид:

∫ ( , ) = ∫ ( , ( ))∙√1 + ( ′( ))2 .

Если кривая задана уравнением в полярных координатах: = ( ), [ ; ] - то формула примет вид:

∫ ( , ) = ∫ [ ( ) , ( ) ]∙√ 2 + ( ′ )2 .

Эти формулы являются следствием формул длины плоской кривой при различных способах задания этой кривой ([4], . ):

| | = ∫

| | = ∫ √1 + ( ′( ))2

| | = ∫ √ 2

+ ( ′ )2

√

( ′)2 + ( ′)2

Пример 2.3.

Вычислить криволинейный интеграл 1 рода = ∫

где – отрезок прямой,

соединяющей точки (1; 1)

и (2; 3).

Решение.

Уравнение отрезка прямой линии , проходящей через две заданные точки (1; 1) и

(2; 3) имеет вид (рис. 2.3):

= 2 − 1, [1; 2].

Применим формулу:

∫ ( , ) = ∫ ( , ( ))∙√1 + ( ′( ))2 ,

где = ( ) = 2 − 1,

′( ) = 2.

2 1

(

′)2

∫ =

∫1 ∙√1 +

= ∫1 (2 −1)∙√5 =

= √5∙∫1

= √5∙∫1 (

−

) =

(2 −1)

2 −1

∙ (

2 −1

) |2

= √5

= √5∙(

− 1) = √5

∙ 1,5.

Рис. 2.3. Иллюстрация

к Примеру 2.3

Ответ:

= √5∙ 1,5.

2.3. Приложения криволинейного интеграла 1 рода

Физические приложения

Масса кривой:

= ∫ ( , , ) - для пространственной кривой,

= ∫ ( , ) - для плоской кривой,

где ( , , ) или ( , ) - линейная плотность массы, распределенной вдоль кривой .

Электрический заряд кривой:

= ∫	(, , ) - для пространственной кривой,
= ∫	(, ) - для плоской кривой,

где ( , , ) или ( , ) - линейная плотность заряда, распределенного вдоль кривой .

Геометрические приложения

Длина кривой: \| \| = ∫	1∙ .
Длина кривой: \| \| = ∫	1∙ .
Площадь цилиндрической поверхности:
(цил.) = ∫ ( ) =	∫ ( , ) .		= ( , )
(цил.) = ∫ ( ) =	∫ ( , ) .

Здесь цилиндрическая поверхность цил.
(рис. 2.4) задается условиями:
- образующая параллельна оси ;
- направляющей служит кривая , лежащая				цил.
- направляющей служит кривая , лежащая
в плоскости ;
в плоскости ;
- сверху поверхность ограничена кривой:
- сверху поверхность ограничена кривой:
= ( , )		Рис. 2.4. Площадь цилиндрической
{ ( , ) .			поверхности

Механические приложения

Статические моменты плоской кривой относительно координатных осей и :

= ∫	)	,	= ∫	)	.
= ∫	∙(,	,	= ∫	∙(,	.

Статические моменты пространственной кривой относительно координатных плоскостей , и :

∫

)

∫

)

∫

)

∙(, ,

Координаты центра тяжести (0, 0) - плоской кривой

и (0, 0, 0) -

пространственной кривой:

∙ ,

∙

- для плоской кривой;

∙ ,

∙

- для пространственной кривой.

Моменты инерции плоской кривой относительно осей координат , и

точки - начала координат:

∫

)

∫

)

= + = ∫ (

)

∙(, ,

∙(,

Моменты инерции пространственной кривой относительно координатных плоскостей , и , относительно координатных осей , и и относительно точки - начала координат:

= ∫

)

∫

)

= ∫

)

∙(, , ,

∙(, ,

∫ (2 + 2)(, , ) ,

∫

( 2 + 2)(, , ) ,

∫ ( 2 + 2)(, , ) ,

( + + ) =

∫

( 2 + 2 + 2)∙(, , ) .

Пример 2.4.

Найти длину одного витка винтовой линии

= ∙

[0; 2 ] (рис. 2.5).

: { = ∙ ,

= ∙

Решение.

Применим формулу: | | = ∫

1∙ ,

где = √(′)2 + (′)2 + (′)2 . Здесь имеем:

′ = −∙ ,

′

Рис. 2.5. К Примеру 2.4

= ∙ ,

= ,

= √2 + 2

В результате получим: | | = ∫02 √2 + 2

= 2∙√2 + 2

Ответ: | | = 2∙√2 + 2

Пример 2.5.

Найти площадь боковой поверхности

прямого кругового цилиндра с радиусом

основания и высотой .

Решение.

Введем систему координат так, чтобы

основание цилиндра лежало в плоскости ,

начало координат совпадало с центром круга, а ось

была параллельна образующей цилиндра (рис. 2.6).

Рис. 2.6. К Примеру 2.5

Направляющей цилиндрической поверхности

будет окружность радиуса . Ограничивающая сверху кривая имеет уравнение:

= ( , ) = , где ( , ) .

Следовательно, получаем:

(цил.) = ∫

( , ) = ∫ = ∙∫

= ∙| | = 2∙ .

Ответ: бок.

цил. = 2∙ .

Пример 2.6.

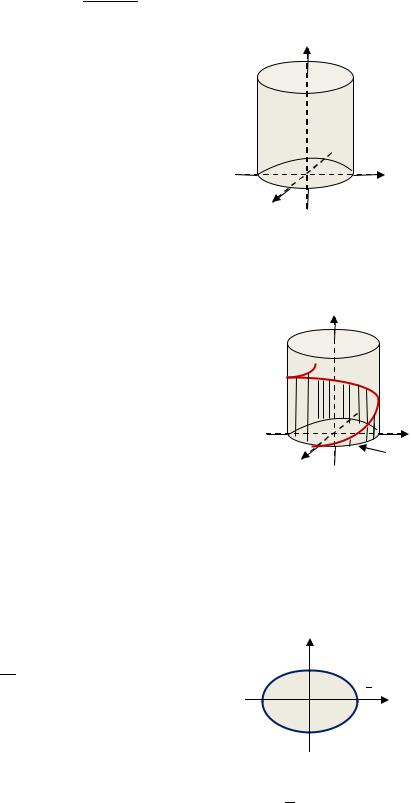
Найти площадь той части боковой поверхности

прямого кругового цилиндра, которая лежит «под»

= ∙

винтовой линией: { = ∙ sin , [0; 2 ] (рис. 2.7).

= ∙

Рис. 2.7. К Примеру 2.6

Решение.

= ∙

( , ) = [ = ∙ sin ] = ∫02 ∙ √

(цил.) = ∫

(′)2

+ (′)2

= ∙

= ∫0 ∙ √(− ∙ sin )

+ ( ∙

= ∙ ∫0

= 2

Ответ: (

) = 22

цил.

Пример 2.7.

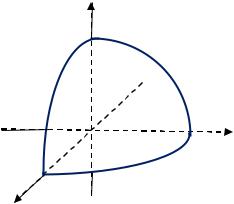
Найти массу эллипса 2 + 2 = 1, если

плотность массы в точке ( , ) равна (, ) = | |.

Решение.

Учитывая симметричность эллипса относительно осей координат (рис. 2.8) и четность функции | |, можно найти массу четверти эллипса и умножить результат на 4.

√2

Рис. 2.8. К Примеру 2.7

Эллипс можно задать параметрическими уравнениями: { = √2 ∙ , [0; 2 ].

Применим формулу для вычисления массы:

( , ) = ∫

= ∫

( ( ), ( ))∙√

(′)2 + (′)2

Вычислим массу первой четверти эллипса:

( ( ), ( ))∙√

(′)2 + (′)2

= ∫

( )∙√

(′)2

+ (′)2

= ∫2

																																( ) = ∫1
					∙√22 + 2																		= − ∫			√2 − 2									√2 − 2					=
		= ∫2			∙√22 + 2																		= − ∫		2	√2 − 2									√2 − 2					=
				0																				0										0
											1											) \|10 =		1				1			+		1	= 4∙(				1	) = + 2.
= (									+		1	∙ √2 − 2												1			+	1	=				1				+	1
											2
					√2																				√2			2		4
					√2																				√2			2		4	2				4			2
Ответ: = + 2.
Пример 2.8.
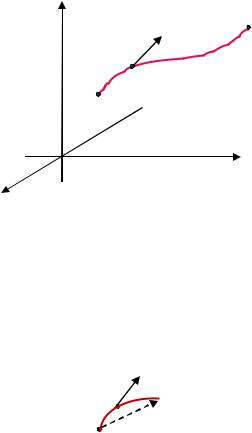
		Найти координаты центра масс контура
однородного сферического треугольника,
однородного сферического треугольника,
расположенного в первом октанте (рис. 2.9):																																2						1
	2	+	2	+			2			=			2	, ≥ 0, ≥ 0, ≥ 0.																		2
		+		+						=				, ≥ 0, ≥ 0, ≥ 0.
Решение.
		Пусть (0, 0, 0) - центр масс


заданного контура. Применим формулы:
заданного контура. Применим формулы:
		=					1		∙					=		1			∙∫ ∙(, , ) ,
							1									1
																																				3
			0																																	3

								1										1			∙∫ ∙(, , ) ,
		=						1		∙					=			1
		=								∙					=
				0

		=				1				∙					=		1			∙∫ ∙(, , ) ,												Рис. 2.9. К Примеру 2.8
		=								∙					=					∙∫ ∙(, , ) ,
			0

= ∫ ( , , ) .

Учитывая, что контур – однородный, т.е. ( , , ) = = , получаем:

= ∫

= ∙∫

= ∙| |,

∙∫

∙ =

∙ ∫

∙∫

∙| |

| |

∙∫

∙ =

∙ ∫

∙∫

∙| |

| |

∙∫

∙ =

∙

∫

∙∫

∙| |

| |

Вычислим ∫

. Разобьем контур на три кривые: = 1 2 3, где

{

2 + 2 = 2

: {

2 + 2 = 2

: {

+ 2

= 2

- четверти окружностей радиуса ;

= 0

следовательно: | | = 3∙

| |

По свойству аддитивности имеем:

∫

= ∫ 1 + ∫ 2 + ∫ 3 .

∫ 1 = ∫ 1 0 = 0;

{

= ∙

, 0 ≤ ≤

= ∙

∫ 2 = [

] = ∫0 ∙ ∙ = ∙ |0

= ;

= √(′)2 + (′)2 = ∙

= ∙

{ = ∙ ,

0 ≤ ≤ 2

∫

= [

] = ∫

∙ ∙ = 2∙ |2

= 2;

= √(′)2

+ (′)2

= ∙

∫ = 0 + 2 + 2 = 22.

Аналогично получим:

∫

= 22

и ∫

= 22.

Следовательно:

∙∫

∙22 =

| |

Ответ: (

) - центр масс.

2.4. Криволинейный интеграл 2 рода

Вначале рассмотрим задачу, которая приводит к понятию криволинейного интеграла 2 рода.

2.4.1. Задача о вычислении работы переменной силы вдоль кривой

Предположим, что материальная точка перемещается вдоль кривой под

(рис. 2.10).

действием переменной силы

Требуется найти работу , которую

при перемещении точки

( )

совершает сила

из пункта в пункт .

Частный случай этой задачи рассмотрен

в работе [4], . .

Из курса физики известно, что если

сила постоянна (по величине и направлению),

а линия = [ ] - отрезок прямой, то

работа равна скалярному произведению

вектора силы на вектор перемещения:

Рис. 2.10. Перемещение точки

= ∙ = | |∙| |∙ ,

вдоль кривой

где - угол между векторами

Для решения задачи в общем случае разобьем кривую на частичные дуги

точками ≡ , , … ,

−1

≡ :

- дуга

(

), = 1 ÷ .

…

где

−1

Далее на каждой частичной дуге выберем произвольную точку ̆ , = 1 ÷ (рис. 2.11).

Если частичные дуги имеют достаточно малые размеры, то вектор силы на этом участке можно считать постоянным и равным ( ), а дугу (−1 ) - можно считать отрезком прямой.

Тогда работа силы на этом участке приближенно равна: ≈ ( )∙∆ ,

( )

∆

−1

Рис. 2.11. Вычисление

работы на частичных дугах

где			,	= 1 ÷ .
где	∆	=	,	= 1 ÷ .
		−1
	Вся работа			равна сумме работ на частичных участках:

= ∑=1 ≈ ∑=1 ( )∙∆ .

Это приближенное равенство тем точнее, чем меньше размеры частичных дуг или модули векторов ∆ , = 1 ÷ ; другими словами, чем меньше ранг разбиения

λ = |∆ |, тем точнее эта приближенная формула.

1≤ ≤

В пределе при λ → 0 получим точное равенство:

=		∑
=		∑	=1	(	)∙∆ .
	λ → 0		=1
	λ → 0

2.4.2. Понятие криволинейного интеграла 2 рода

Пусть = ̆ - простая кривая на плоскости или в пространстве, на которой задана вектор - функция ( ), . Выберем направление на кривой, идущее от точки

к точке . Выполним следующие действия.

1. Разбиение кривой на частичные дуги точками 0 ≡ , 1, … , −1, ≡ :

		̆		̆		̆	(рис. 2.12),
	= 1		2 …				(рис. 2.12),
где	̆	- дуга			(	),	= 1 ÷ .
где		- дуга			(	),	= 1 ÷ .
					−1
2. Выбор промежуточных точек:
			̆		, = 1 ÷ .
					, = 1 ÷ .

3. Вычисление скалярных произведений векторов:

						,	= 1 ÷ ,
			(		) ∙ ∆	,	= 1 ÷ ,

где				– вектор, соединяющий
где	∆	=	−1	– вектор, соединяющий
			−1

начало и конец дуги (−1 ), и вычисление интегральной суммы:

= ∑=1 ( )∙∆ .

Пусть λ =
	\|∆ \| - ранг разбиения.
1≤ ≤

−2 −1

Рис. 2.12. Разбиение кривой

Определение 2.3.

Число называется пределом интегральных сумм при λ → 0, если для > 0> 0 такое, что для любого разбиения кривой с рангом разбиения λ < и при любом выборе промежуточных точек { }=1 выполняется неравенство:

		\|	− \| < .

Запись: =	- означает, что при λ → 0 этот предел существует, он не
	λ → 0

зависит ни от способа разбиения, ни от выбора промежуточных точек, и равен числу .

Определение 2.4.

Конечный предел интегральных сумм при λ → 0 называется

криволинейным интегралом 2 рода (или криволинейным интегралом по координатам)

от вектор-функции ( ) вдоль кривой .

Обозначение: ∫		(	)	Следовательно, по определению имеем:
Обозначение: ∫			∙.	Следовательно, по определению имеем:
	∫					∑				.
	∫	( ) ∙ =				∑	=1	(	) ∙ ∆	.
					λ → 0		=1

Запишем криволинейный интеграл 2 рода в координатной форме.

В случае пространственной кривой вектор-функция ( ) задается тремя координатными функциями:


( ) = (, , )∙ + (, , )∙ + (, , )∙ .


Пусть = - радиус-вектор точки ( , , ) , тогда имеем:
∆

∆ = (∆ ) = ∆ ∙ + ∆ ∙ + ∆ ∙				и = ( ) = ∙ + ∙ + ∙ ,
∆

( )∙ = (, , ) + (, , ) + (, , ) .
В этом случае криволинейный интеграл 2 рода запишется в виде:
∫
∫	( ) ∙ = ∫ (, , ) + (, , ) + (, , ) .
В случае плоской кривой получим:
	( , )
( ) = (( , ))			= (, )∙ + (, )∙ ,		= ( ) = ∙ + ∙ ,

	( )∙ = (, ) + (, ) ,
	∫
	∫	( )∙ = ∫ (, ) + (, ) .

Таким образом, согласно определению имеем:

∫

( , , ) + ( , , ) + ( , , ) =

∑

{ ( , , )∆ + (

, ,

)∆

+ (

, ,

)∆ };

λ → 0

∫ ( , ) + ( , ) =

∑

{ ( , )∆ + ( ,

)∆

λ → 0

Вектор-функция ( ), для которой существует криволинейный интеграл 2 рода, называется интегрируемой вдоль кривой .

Пример 2.9.

∫				0 = 0	∫
∫	0∙ =	∑=1	0∙∆ =	0 = 0	∫	0∙ = 0,
		λ → 0		λ → 0
		λ → 0		λ → 0

т.е. криволинейный интеграл 2 рода от нулевой вектор-функции равен нулю. Физический смысл криволинейного интеграла 2 рода.

Криволинейный интеграл 2 рода от вектор-функции ( ) вдоль кривой равен работе , совершаемой силой по перемещению материальной точки вдоль кривой :

( )∙ .= ∫

Пример 2.10.

		вдоль
Найти работу силы ( ) = (, )∙

плоской кривой , лежащей в плоскости (рис. 2.13).

Решение.

= ∫			∑
= ∫	( )∙ =		∑	=1	(	)∙∆ .
		λ → 0		=1

Здесь вектор силы ортогонален вектору перемещения:

( )

Рис. 2.13. К Примеру 2.10

Ответ: = 0.

Условия существования криволинейного интеграла 2 рода от вектор-функции (интегрируемости вектор-функции) сформулированы в следующем утверждении. Теорема 2.5 (достаточное условие интегрируемости).

Пусть - простая гладкая кривая, а вектор-функция ( ) - непрерывна на кривой

(непрерывны все ее координатные функции). Тогда ( ) интегрируема вдоль кривой .

Доказательство этой теоремы есть в работе [1].

2.4.3. Свойства криволинейного интеграла 2 рода

Пусть вектор-функции

( ) и ( ) - интегрируемы вдоль кривой . Тогда

справедливы следующие свойства.

1. Антисимметричность.

При изменении направления кривой криволинейный интеграл 2 рода

меняет знак:

∫̆

(

)

(

)

∙ = − ∫̆

∙ .

2. Линейность.

а) постоянный множитель можно выносить за знак криволинейного интеграла 2 рода:

∫

(

)

(

)

( ∙

)∙ = ∙∫

∙ , = ;

б) криволинейный интеграл 2 рода от суммы вектор-функций равен сумме криволинейных интегралов 2 рода от этих вектор-функций:

(		)	(	)		(	)	(	)
∫ (			+		)∙ = ∫		∙ + ∫		∙ .

Свойство линейности можно записать в следующем виде:

∫	(		)	(	)		(	)	(	)	1, 2 = .
∫	(1 ∙			+ 2 ∙		)∙ = 1∙∫		∙ + 2∙∫		∙	1, 2 = .

3. Аддитивность.

Если кривая разбита на две дуги, то криволинейный интеграл 2 рода по всей кривой равен сумме криволинейных интегралов 2 рода по каждой из этих дуг:

∫

(

)

(

)

(

)

∙ =

∫ 1

∙ + ∫ 2

∙ ,

где = 1 2

∩ 2 = .

Доказательство.

∫

( )∙ = ∑

(

)∙

−1

λ → 0

∫

;

так как

, = 1 ÷ , то

( )∙ = ∑

(

)∙

= −

−1

λ → 0

получаем:

∫̆ ( )∙ = − ∫̆

( )∙ .

∫

(

∑

(

) +

∙ ( ) +

∙ ( ))∙ =

∙ (

∙ ( ))∙∆ =

λ → 0

= ∑

(

)

∙ (

) ∙ ∆

∙ (

∙ ∆ ) =

λ → 0

= (∑

∑

∙ ( )

∙ ∆

∙ ( )

∙ ∆ ) =

λ → 0

∑

+ ∑

∙ (

)∙∆

∙ (

)∙∆

λ → 0

= ∙

∑

+ ∙ ∑

(

)∙∆

(

)∙∆

1 λ → 0

λ → 0

= 1∙∫

( )∙ + 2∙∫

( )∙ .

на частичные дуги, чтобы

Рассмотрим такое разбиение кривой =

…

точка пересечения

оказалась бы одной из точек разбиения .

Введем

обозначения интегральных сумм:

( ) = ∑

- по кривой ;

( )∙∆

(1)

(

)

= ∑

- по дуге ;

(

)∙∆

(2)

(

)

= ∑

- по дуге .

= +1

(

)∙∆

Тогда имеем: ( ) = (1)( )

+ (2)(

Переходя к пределу в этом равенстве при λ → 0, получим:

∫

(

)

(

)

(

)

∙ = ∫ 1

∙ + ∫ 2

∙ .

2.4.4. Вычисление криволинейного интеграла 2 рода

Вычисление криволинейного интеграла 2 рода, как и криволинейного интеграла 1 рода, сводится к вычислению определенного интеграла.

Теорема 2.6.

Пусть простая гладкая кривая = ̆ - задана параметрическими уравнениями:

= ( )

{ = ( ), [ ; ], где ( ), ( ), ( ) - непрерывно-дифференцируемые функции на

= ( )

отрезке [ ; ], причем ( ( ), ( ), ( )), ( ( ), ( ), ( )).

		14
Пусть вектор-функция		- непрерывна
	( ) = ( , , )∙ + ( , , )∙ + ( , , )∙

на кривой , т.е. непрерывны функции ( , , ), ( , , ) и ( , , ) при ( , , ) .

Тогда справедливо равенство:

∫ ( , , ) + ( , , ) + ( , , ) = . = ∫ { ( ( ), ( ), ( )) ∙ ′( ) + ( ( ), ( ), ( )) ∙ ′( ) + ( ( ), ( ), ( )) ∙ ′( )}

Доказательство этой теоремы также можно найти в работе [1].

Вслучае плоской кривой = ̆ : { = ( ), [ ; ] – получаем формулу:

= ( )

∫ ( , ) + ( , ) = ∫ { ( ( ), ( )) ∙ ′( ) + ( ( ), ( )) ∙ ′( )} .

Если плоская кривая = ̆ - задана явным уравнением: = ( ), [ ; ], или= ( ), [ ; ] - то формула принимает вид:

∫ ( , ) + ( , ) = ∫ { ( , ( )) + ( , ( )) ∙ ′( )} , или

∫ ( , ) + ( , ) = ∫ { ( ( ), ) ∙ ′( ) + ( ( ), )} .

Пример 2.11.

Вычислить криволинейный интеграл 2 рода:

= 3

= ∫ ( + ) + 2 + , где : { = 2, [0; 1].=

Решение.

= ∫ ( + ) + 2 + = ∫1{( 3 + 2) ∙ 3 2 + 2 ∙ 2 + 5 ∙ } =
														0
= ∫1(4 5		+ 3 4 + 4 2) = (						2 6				+	3 5	+	4 3			) \|10 = 2				3		.
= ∫1(4 5		+ 3 4 + 4 2) = (										+	5	+				) \|10 = 2						.
	0						3						5	3							5
Ответ: = 2			3	.
Ответ: = 2		5		.
		5
Пример 2.12.

	Вычислить криволинейный интеграл 2 рода:
= ∫	2 −				2	- вдоль различных кривых,																								1
= ∫	2 −					- вдоль различных кривых,																								1
соединяющих точки (0; 0) и (2; 1):																																							2
	а) прямая [ ],																																						2
	б) парабола с осью ,
	в) ломаная [ ], где (2; 0) (рис. 2.14).																								Рис. 2.14. К Примеру 2.12
																									Рис. 2.14. К Примеру 2.12
Решение.
	а) Отрезок прямой линии [ ] задается уравнением: =																														1		,			[0; 2].
	а) Отрезок прямой линии [ ] задается уравнением: =																													2			,			[0; 2].
																														2
Следовательно, имеем:
= ∫	(2 − 2 ) = ∫2						(2 ∙		1		− 2 ∙					1			) =		1		∙∫2 2					=							1		∙	3	\|02 = 1	1	.
= ∫	(2 − 2 ) = ∫2						(2 ∙				− 2 ∙								) =				∙∫2 2					=							2		∙		\|02 = 1		.
						0	2							2							2				0										2		3			3
	б) Дуга параболы с осью задается уравнением:																								=				1	2,							[0; 2].				Значит:
	б) Дуга параболы с осью задается уравнением:																								=			4		2,							[0; 2].				Значит:
																												4
= ∫	(2 − 2 ) = ∫02 (2 ∙								1	2 − 2 ∙							1			) = ∫02 (						1	3 −							1		3) = ∫02 0 = 0.
= ∫	(2 − 2 ) = ∫02 (2 ∙								4	2 − 2 ∙							2			) = ∫02 (						2	3 −							2		3) = ∫02 0 = 0.
	в) Ломаная линия [ ] разбивается на два отрезка:
= 1 2, где 1 = [ ]:							{0 ≤ ≤ 2,							2 = [ ]: {										= 2								. Следовательно:
							= 0														0 ≤ ≤ 1

<<< < Предыдущая 1 2 3 45 / 135 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в папке Экзамен

#
05.06.2021154.18 Кб8Вопросы к экзамену.pdf
#
05.06.202110.65 Mб17Все лекции.pdf
#
05.06.2021101.62 Кб6Дополнительные вопросы.pdf