
21
= ∫0 −2 ∙∫0 −2 = (∫0 −2 )2. Устремляя к бесконечности, получим:
|
|
|
|
|
|
|
|
2 |
= (∫+∞ −2 |
)2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= |
(∫ −2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
→ +∞ |
|
→ +∞ |
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Окружим квадрат |
четвертями кругов и |
|
|
|
|
|
(рис. 1.23): |
|
|
|
. |
|||||||||||||||||||||||||
|
√2 |
√2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Так как −(2+ 2) > 0 |
( , ), то по свойствам двойного интеграла (см. 1.2.2, |
|
||||||||||||||||||||||||||||||||||
Следствие 1.4) имеем: |
−(2+ 2) ≤ |
−(2+ 2) ≤ |
|
|
|
−(2+ 2) . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Используем результат Примера 1.11: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
−(2+ 2) = |
|
(1 − −2), |
|
|
|
−(2+ 2) = |
|
(1 − −22). |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
√2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Следовательно, имеем неравенства: |
|
(1 − −2) ≤ |
≤ |
|
(1 − −22). |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Переходя к пределу в этих неравенствах при значениях → +∞, получим: |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|||||
|
|
≤ (∫+∞ |
−2 ) |
≤ |
, |
т.е. (∫+∞ −2 ) = |
|
, |
или ∫+∞ −2 |
= |
. |
|
|
|
|||||||||||||||||||||||
|
4 |
4 |
4 |
|
|
|
|
||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||
Формула доказана.
1.5. Тройной интеграл и его свойства
Теория тройного интеграла аналогична теории двойного интеграла. Если двойной интеграл является обобщением понятия определенного интеграла на случай функции 2-х переменных, то тройной интеграл является его обобщением на случай функции 3-х переменных.
1.5.1. Понятие тройного интеграла
Пусть имеется функция = ( , , ), заданная на множестве Ω 3, где Ω – пространственная замкнутая область – тело, ограниченное гладкой (или кусочно-гладкой) поверхностью (рис. 1.24).
Выполним следующие действия.
1. Разбиение области Ω на частичные области: Ω = Ω1 Ω2 … Ω .
2. |
|
Выбор промежуточных точек: ( , , ) Ω |
|
, |
= 1, 2, … , (рис. 1.24). |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
Вычисление суммы: = |
∑ |
( |
, |
, |
) ∙ ∆ |
, |
|
где ∆ |
= (Ω ) – объем |
||
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
частичной области Ω , = 1, 2, … , . |
|
|
Z |
|
|
|
|||||||
|
|
Сумма |
называется |
|
|
|
|
|
|
Ω |
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интегральной суммой Римана |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функции ( , , ) по области Ω. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
Заметим, что интегральная сумма |
|
|
|
|
|
|
Ω |
||||
зависит не только от значения , |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
но и от способа разбиения области Ω |
|
|
|
|
|
|
|
|
|||||
на частичные области Ω и от выбора |
|
|
|
|
|
|
|
|
|||||
промежуточных точек |
|
|
|
|
|
|
|
|
|
||||
( , , ) Ω , = 1, 2, … , . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
|
||
|
|
Введем обозначения: |
|
|
|
|
|
Y |
|||||
|
|
|
|
|
|
|
|
|
|
||||
– диаметр частичной области Ω , |
|
|
|
|
|
|
|
|
|||||
= 1, 2, … , ; |
|
|
|
X |
|
|
|
|
|
|
|||
λ = {1, … , } - ранг разбиения. |
|
|
Определение 1.5. |
Рис. 1.24. Иллюстрация к |
|
Число называется пределом |
||
понятию тройного интеграла |
||
|
22
интегральных сумм при λ → 0, если для > 0 > 0 такое, что для любого разбиения области Ω с рангом разбиения λ < и при любом выборе промежуточных точек { }=1 выполняется неравенство:
|
| |
− | < . |
|
|
|
|
|
Запись: = - означает, что при |
λ → 0 этот предел существует, он не |
||
λ → 0 |
|
|
|
зависит ни от способа разбиения, ни от выбора промежуточных точек, и он равен числу .
Определение 1.6.
Конечный предел интегральных сумм |
|
при λ → 0 называется тройным |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интегралом от функции ( , , ) по области Ω. Обозначение: |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
( , , ) = |
|
∑ |
|
( , , |
) ∙ ∆ |
или: |
||||||
|
Ω |
|
λ → 0 |
|
=1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
( ) = |
∑ |
|
( ) |
∙ ∆ |
. |
|
|
|||
|
|
Ω |
λ |
→ 0 |
=1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
Функция ( , , ), для которой существует тройной интеграл, называется интегрируемой по области Ω. Область Ω называется областью интегрирования.
Пример 1.12.
|
0 = ∑=1 |
0∙∆ = ∑=1 |
0 = 0 = 0 |
0 = 0 |
. |
Ω |
λ → 0 |
λ → 0 |
λ → 0 |
Ω |
|
Физический смысл тройного интеграла.
Если ( , , ) - пространственная плотность массы, распределенная по телу Ω,
то = Ω ( , , ) - масса всего неоднородного тела.
Если ( , , ) - плотность электрического заряда, распределенная по телу Ω,
то = Ω ( , , ) - заряд всей области Ω.
1.5.2. Условия интегрируемости функции
Теорема 1.10.
Если функция ( , , ) интегрируема по области Ω, то она ограничена в области Ω. Доказательство этого утверждения аналогично случаю двойного интеграла.
Обратное утверждение неверно: есть ограниченные, но не интегрируемые функции.
Следствие 1.7.
|
|
Если функция ( , , ) не ограничена в области Ω, то она и не интегрируема по |
||||||||||||||||||||
этой области. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Для получения признаков интегрируемости функции ( , , ) по области Ω, как и |
||||||||||||||||||||
в случае двойного интеграла, вводится понятие суммы Дарбу́. |
|
|
|
|
|
|
||||||||||||||||
|
|
Для произвольного разбиения |
{Ω |
} |
области Ω введем обозначения: |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= { ( ), Ω |
}, |
= { ( ), Ω }, |
|
|
= |
− |
|
, = 1, … , . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Очевидно, что |
|
≤ ( ) ≤ |
|
Ω , |
= 1, … |
, . |
Величина |
|
называется |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
колебанием функции ( ) в частичной области Ω , = 1, … , . |
|
|
|
|
|
|||||||||||||||||
Определение 1.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пусть ∆ = (Ω ) – объем частичной области Ω , |
= 1, … , . Тогда величины: |
|||||||||||||||||||
|
|
|
= |
∑ |
|
|
∙∆ и = ∑ |
∙∆ |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
=1 |
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
||
называются интегральными суммами Дарбу - соответственно нижней интегральной суммой и верхней интегральной суммой.
23
Очевидно, что для любого разбиения {Ω }=1 области Ω и любого выбора точек { }=1 интегральная сумма Римана находится между значениями интегральных сумм Дарбу:
≤ ≤
Теорема 1.11 (основной признак интегрируемости).
Для того чтобы ограниченная функция ( ) была интегрируема по области Ω,
необходимо и достаточно, чтобы ( − ) = 0.
λ→0
Доказательство этой теоремы есть в работе [1].
Разность − можно выразить через колебания функции ( ):
− = ∑=1 ∙∆ − ∑=1 ∙∆ = ∑=1( − )∙∆ = ∑=1 ∙∆ .
В терминах колебаний функции ( ) основной признак интегрируемости можно сформулировать следующим образом.
Следствие 1.8 (основной признак интегрируемости).
Для того чтобы ограниченная функция ( ) была интегрируема по области Ω, необходимо и достаточно, чтобы для > 0 > 0 такое, что для любого разбиения {Ω }=1 области Ω с рангом разбиения λ < и при любом выборе промежуточных точек
{ }=1 - выполнялось неравенство: ∑=1 ∙∆ < .
Классы интегрируемых функций.
Из основного признака интегрируемости можно установить классы функций, интегрируемых по заданной области.
Теорема 1.12.
Если функция ( ) непрерывна в области Ω, то она и интегрируема по области Ω. Доказательство аналогично случаю двойного интеграла.
Оказывается, интегрируемость сохраняется и для класса ограниченных функций, непрерывных «почти всюду» в области интегрирования.
Теорема 1.13.
Если функция ( ) ограничена в области Ω и непрерывна в области Ω всюду за исключением конечного числа точек или конечного числа кривых или поверхностей, лежащих в этой области, то она интегрируема по области Ω.
Доказательство этой теоремы есть в работе [1].
Замечание 1.7.
Интегрируемость функции и величина интеграла сохраняются, если произвольным образом изменить значения функции в конечном числе точек или на конечном числе кривых или поверхностей, лежащих в этой области.
Это связано с тем, что объемы всех поверхностей и кривых равны нулю, поэтому соответствующие слагаемые в интегральных суммах не влияют на общую сумму.
1.5.3. Свойства тройного интеграла
Свойства тройного интеграла аналогичны свойствам двойного интеграла.
Свойства, выраженные равенствами. 1. Нормированность.
Тройной интеграл от единицы по заданной области равен объему этой области:
Ω = (Ω) |
(или Ω = (Ω)). |
2. Линейность.

24
Пусть функции ( ) и ( ) интегрируемы по области Ω. Тогда а) постоянный множитель можно выносить за знак тройного интеграла:
Ω ∙( ) = ∙ Ω ( ) , = ;
б) тройной интеграл от суммы функций равен сумме тройных интегралов от этих функций:
Ω ( ( ) + ( )) = Ω ( ) + Ω ( ) .
Свойство линейности можно записать в следующем виде:
|
(1 ∙ ( ) + 2 |
∙ ( )) = 1∙ |
( ) + 2∙ |
( ) |
1, 2 = . |
Ω |
|
Ω |
Ω |
|
|
3. Аддитивность.
Пусть функция ( ) интегрируема по области Ω.
Если область интегрирования разбита на две области, то тройной интеграл по всей области равен сумме тройных интегралов по каждой из этих областей:
|
|
Ω ( ) = Ω1 ( ) + Ω2 ( ) , |
|
где Ω = Ω1 Ω2, |
Ω1 ∩ Ω2 = (или это пересечение состоит из конечного числа |
||
кривых и поверхностей). |
|
||
Доказательство этих свойств проводится аналогично доказательству для двойного |
|||
интеграла. Например, свойство нормированности: |
|||
= ∑ =1 1∙∆ = ∑ =1 ∆ = (Ω) = (Ω). |
|||
Ω |
λ → 0 |
λ → 0 |
λ → 0 |
Свойства, выраженные неравенствами. |
|
||
Пусть функции ( ) и ( ) интегрируемы по области Ω. |
|||
1. Интегрирование неравенств. |
|
||
Если ( ) ≥ ( ) Ω, то и |
Ω ( ) ≥ Ω ( ) . |
||
Следствие 1.9. |
|
|
|
Если ( ) ≥ 0 |
Ω, то и Ω ( ) ≥ 0. |
||
Следствие 1.10. |
|
|
|
Пусть ( ) ≥ 0 |
Ω; тогда для любых областей Ω1, Ω2 Ω справедливо |
||
утверждение: |
|
|
|
|
Ω1 Ω2 ( ) ≤ ( ) |
||
|
|
Ω1 |
Ω2 |
(т.е. при расширении области интегрирования тройной интеграл возрастает).
Следствие 1.11.
| Ω ( ) | ≤ Ω |( )|.
2. Оценки тройного интеграла.
Если значения подынтегральной функции ( ) в области Ω ограничены величинами и , то значение тройного интеграла ограничено величинами∙(Ω) и ∙(Ω), где (Ω)- объем области Ω:
≤ ( ) ≤ Ω ∙(Ω) ≤ Ω ( ) ≤ ∙(Ω).
Пример 1.13.
1
Оценить значение тройного интеграла: = Ω 4 ( 2 + 2+ 2+ 9) ,
где Ω - шар: 2 + 2 + 2 ≤ 9.
Решение.

25
Так как |
(Ω) = |
4 |
∙ |
3 |
= |
|
4 |
∙3 |
3 |
= 36, а значения подынтегральной функции |
|||||||||||
3 |
|
3 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
1 |
|
≤ |
1 |
|
≤ |
1 |
1 |
||||
удовлетворяют неравенствам: |
|
∙ |
|
|
|
|
|
∙ |
|
, то получаем оценки: |
|||||||||||
4 |
18 |
4 ( 2 + 2+ 2+ 9) |
4 |
9 |
|||||||||||||||||
41 ∙181 ∙36 ≤ ≤ 41 ∙19∙36 12 ≤ ≤ 1. Ответ: 0,5 ≤ ≤ 1.
Теоремы о среднем значении. Теорема 1.14.
Пусть функция ( ) интегрируема по области Ω и пусть
= { ( ), Ω}; = { ( ), Ω}. Тогда [ ; ]:
Ω ( ) = ∙(Ω).
Число = (1Ω)∙ Ω ( ) - называется интегральным средним значением
функции ( ) в области Ω.
Теорема 1.15.
Пусть функция ( ) непрерывна в области Ω. Тогда 0 Ω:
Ω ( ) = (0)∙(Ω).
Доказательство этих свойств и теорем проводится аналогично случаю двойного интеграла.
1.6. Вычисление тройного интеграла
Вычисление тройного интеграла Ω ( , , ) начинается с изучения области Ω. Различаются области (или тела́) «правильные» (относительно какой-нибудь координатной оси) и «неправильные».
Пусть функции = 1( , ) |
и = 2( , ) определены и непрерывны в области |
|||
2, |
причем ( , ) ≤ |
2 |
( , ) ( , ) . |
|
|
1 |
|
|
|
Определение 1.8.
Тело Ω, ограниченное снизу поверхностью = 1( , ), сверху - поверхностью= 2( , ), а с боков - цилиндрической поверхностью с образующими, параллельными
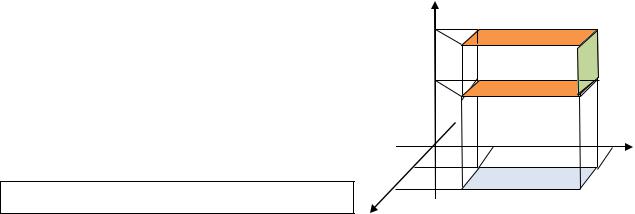
оси , называется «правильным» телом в направлении (относительно) оси (рис. 1.25).
Z |
= 2( , ) |
|
= 1( , ) |
|
|
|
|
|
|
Рис. 1.25. |
Правильное тело |
относительно оси
26
Это тело характеризуются тем, что любая прямая, параллельная оси , пересекает верхнюю и нижнюю границы тела Ω не более чем в двух точках. Проекцией тела Ω на плоскость является область .
Аналогично определяются тела, правильные в направлении осей и . Тело может быть правильным в направлении всех осей координат. Таковым является,
например, прямоугольный параллелепипед, каждая грань которого параллельна одной из координатных плоскостей (рис. 1.26).
Если тело не является правильным ни в каком направлении, то его будем называть
неправильным.
Неправильное тело, как правило, можно разбить на частичные тела так, что каждое из них уже будет правильным в каком-либо направлении.
Для правильных тел вычисление тройного интеграла сводится к вычислению двойного интеграла. Справедливо следующее утверждение, которое приводим без доказательства.
Теорема 1.16.
Пусть функция ( , , ) интегрируема по области Ω, где Ω - правильное тело в направлении оси :
Ω = {( , , ) 3: 1( , ) ≤ ≤ 2( , ), ( , ) }.
Если для любой фиксированной точки ( , ) существует определенный
интеграл ∫ 2( , ) ( , , ) , то существует и повторный интеграл
1( , )
(∫ 2( , ) ( , , ) ) , который равен тройному интегралу:
1( , )
|
( , , ) = |
(∫ 2( , ) |
( , , ) ) |
. |
Ω |
|
1( , ) |
|
|
Если при этом область является правильной областью в 2:
= {( , ): 1( ) ≤ ≤ 2( ), [ ; ]} или: = {( , ): 1( ) ≤ ≤ 2( ), [ ; ]},
то тройной интеграл будет равен трехкратному интегралу:
|
( , , ) = ∫ |
∫ 2() |
∫ 2( ,) |
( , , ) |
|
или: |
|
Ω |
|
( ) |
|
(,) |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
||
|
( , , ) = ∫ |
∫ 2() |
∫ 2( ,) |
( , , ) |
. |
|
|
Ω |
|
1( ) |
1(,) |
|
|
|
|
Аналогичные утверждения имеют место, когда область интегрирования Ω - правильное тело в направлении осей и .
Замечание 1.8.
В случае, когда область интегрирования – прямоугольный параллелепипед:
Ω = { ≤ ≤ , ≤ ≤ , ≤ ≤ }
(рис. 1.26), получаем трехкратный интеграл следующего вида:
Ω ( , , ) = ∫ ∫ ∫ ( , , ) .
Замечание 1.9.
Если при этом подынтегральная функция представима в виде произведения трех функций,
|
|
Ω |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Рис. 1.26. Область интегрирования -
прямоугольный параллелепипед
27
каждая из которых является функцией только одной переменной:
( , , ) = 1( )∙ 2( )∙ 3( ),
то тройной интеграл равен (аналогия с двойным интегралом – см. 1.3.3) произведению трех определенных интегралов:
Ω 1( ) ∙ 2( ) ∙ 3( ) = ∫ 1( ) ∙∫ 2( ) ∙∫ 3( ) .
Пример 1.14.
|
|
|
|
Вычислить = Ω |
3 |
|
2 |
, где Ω = {0 ≤ ≤ 1, 0 ≤ ≤ , |
|
|
|
|
|
|
|
|
} |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 ≤ ≤ . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
= |
∫ |
1 |
|
∫ |
|
∫ |
|
|
3 |
|
2 |
= ∫ |
1 |
∫ |
|
( |
3 |
|
2 2 |
| |
|
) = |
1 |
∫ |
1 |
∫ |
|
|
|
5 |
|
4 |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 |
|
1 |
|
|
|
5 |
|
5 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
10 |
|
|
1 |
|
|
11 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
= |
|
∫ |
|
( |
|
∙ |
|
|
|
|
|
|
|0) = |
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
= |
|
|
|
|
∙ |
|
|
|
|0 = |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
|
5 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Ответ: |
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
+ + = 2 |
||||||||||||||||||||||
Пример 1.15. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Вычислить: = |
|
|
|
( + ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
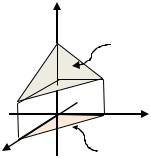
где Ω |
ограничена плоскостями (рис. 1.27): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= 0, = 0, = 1, + + = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ = 1 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
Область интегрирования Ω представляет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
собой треугольную пирамиду с вершиной |
|
|
|
|
Рис. 1.27. |
|
|
Иллюстрация к Примеру 1.15 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в точке (0; 0; 2) с треугольником в основании, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
лежащим в плоскости = 1 и с боковыми гранями, лежащими в координатных |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
плоскостях и |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
Это правильное тело в направлении оси , ограниченное снизу плоскостью = 1, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а сверху - плоскостью = 2 − − . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Следовательно, можно применить формулу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω ( , , ) = |
|
|
2( , ) |
( , , ) ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
(∫ 1( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
В нашем случае получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
= (∫12− − ( + ) ) = |
|
(∫12− − + ∫12− − ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
( (1 − − ) + |
1 |
|
2|12− − ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|||||||||||||
= |
( (1 − − ) + |
|
|
(1 − − )(3 − − )) = ( |
|
− − 2 − |
|
|
|
+ |
|
|
|
) . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
|
2 |
|
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Область является проекцией пирамиды на плоскость и представляет собой |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
треугольник, ограниченный осями координат и прямой + = 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= {0 ≤ ≤ 1, 0 ≤ ≤ 1 − }. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Следовательно, имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
∫1 |
∫1− ( |
3 |
|
− − 2 − |
|
2 |
+ |
|
|
2 |
) = |
∫1 (( |
3 |
|
− − |
2 |
) |1−0 |
+ |
∫1− ( |
2 |
|
− 2 ) ) = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= ∫1 |
(( |
3 |
|
− − |
2 |
) (1 − ) |
+ ( |
3 |
− 2) |1−0 |
) = ∫1 |
( |
3 |
|
− |
5 |
+ |
2 |
+ |
3 |
+ |
|
(1− )3 |
− |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
2 |
2 |
|
|
6 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
−(1 − )2) = ( |
3 |
− |
5 2 |
+ |
|
3 |
+ |
4 |
|
− |
(1− )4 |
+ |
(1− )3 |
) |10 = |
|
|
3 |
− |
5 |
+ |
1 |
+ |
1 |
|
+ |
1 |
|
− |
1 |
|
|
= |
1 |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
24 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
8 |
|
|
24 |
|
3 |
|
4 |
|||||||||||||||||||||||||
Ответ: |
= |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

Пример 1.16.
Найти объем шара радиуса .
Решение.
В декартовой системе координат шар задается неравенством (рис. 1.28):
Ω: 2 + 2 + 2 ≤ 2.
По свойству нормированности имеем:
шара = 2+ 2+ 2≤ 2 .
Шар представляет собой правильное тело в направлении оси , ограниченное
снизу поверхностью = − √2 − 2 − 2 ,
а сверху - поверхностью = √2 − 2 − 2 . Значит, можно записать:
28
= √2 − 2− 2
= − √2 − 2− 2
Рис. 1.28. Вычисление объема шара
|
(∫√ |
2− 2− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|√ |
2− 2− 2 |
|
|
|
|
|
|
||||||||||
= |
|
|
) = |
|
= 2 |
√2 − 2 − 2 |
. |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||
шара |
|
−√ 2− 2− 2 |
|
|
−√ 2− 2− 2 |
|
|
|
|
|
|
|||||||||||
|
Область является проекцией шара на плоскость и представляет собой круг |
|||||||||||||||||||||
с центром в начале координат и радиуса : |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
= {( , ) 2: 2 + 2 ≤ 2}. |
|
|
|
|
|
|
|
|||||||
Для вычисления этого двойного интеграла перейдем к полярным координатам. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= ∙ |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
= ∙ ] = 2 |
|
|
|
|
|
|
|
|||||||
|
= 2 |
|
|
√2 − 2 |
− 2 = [ |
|
′ |
√2 − 2 |
∙ , |
|
||||||||||||
шара |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где ′: { 0 ≤ ≤ . Далее имеем:
0 ≤ ≤ 2
шара = 2∫02 ∫0 √2 − 2 ∙ = − ∫02 ∫0 √2 − 2 (2 − 2) = = − 23 ∫02 (2 − 2) 32 |0 = 23 ∫02 3 = 23 3∙2 = 43 3.
Ответ: шара = 43 3.
1.7. Замена переменных в тройном интеграле
Пусть дан тройной интеграл Ω ( , , ) , где область Ω ограничена кусочно-гладкой поверхностью, а функция ( , , ) непрерывна в этой области или ограничена и непрерывна всюду за исключением конечного числа точек и конечного числа кусочно-гладких кривых и поверхностей, лежащих в этой области.
Рассмотрим преобразование, связывающее переменные ( , , ) с переменными ( , , ) некоторой системой уравнений:
= ( , , )
( ){ = ( , , ).
= ( , , )
Предполагается, что это преобразование устанавливает взаимно-однозначное соответствие между точками области Ω, лежащей в пространстве и точками области Ω′, лежащей в пространстве .
Взаимно-однозначное соответствие означает, что система уравнений ( ) однозначно разрешима относительно новых переменных ( , , ), т.е. выполняются следующие равенства:

29
= ( , , )
{= ( , , ) .
= ( , , )
1.7.1.Якобиан преобразования
Пусть функции = ( , , ), = ( , , ) и = ( , , ) - непрерывно-
дифференцируемы в области Ω′. Составим определитель 3-го порядка из частных производных этих функций:
|
|
|
|
|
|
|
|
|
|||
′ |
′ |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
( , , ) = | ′ |
′ |
′ |
| = |
|
|
. |
|||||
| |
|
|
|
||||||||
|
|
|
|
|
| |
||||||
′ |
′ |
′ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определитель ( , , ) называется определителем Якоби или якобианом. Справедлива следующая лемма (приводим без доказательства).
Лемма 1.2.
Если ( , , ) ≠ 0 в любой внутренней точке области Ω′, то преобразование ( ) устанавливает взаимно-однозначное соответствие между областями Ω и Ω′.
Используя утверждение леммы, можно сформулировать следующую теорему. Теорема 1.17 (о замене переменных в тройном интеграле).
= ( , , ) |
|
Если при замене переменных { = ( , , ) |
якобиан ( , , ) не обращается в |
= ( , , ) |
|
нуль ни в какой внутренней точке области Ω′, то имеет место следующая формула:
Ω ( , , ) = Ω′ ( ( , , ), ( , , ), ( , , )) ∙ |( , , )| .
Доказательство этой теоремы есть в работе [1].
Оформление решения при замене переменных в тройном интеграле выглядит так:
|
= ( , , ) |
|
|
= ( , , ) |
|
Ω ( , , ) = |
= ( , , ) |
= Ω′ ̃( , , ) ∙ |( , , )|, |
|
= |
|
|
[= |( , , )| ] |
|
где ̃( , , ) = ( ( , , ), ( , , ), ( , , )).
Из приведенной формулы следует, что при замене переменных нужно не только подставить в подынтегральную функцию новые переменные, но еще и умножить значение функции на модуль якобиана.
Как и в случае двойного интеграла получаем следующие утверждения. Следствие 1.12 (объем тела в криволинейных координатах).
(Ω) = Ω′|( , , )| = | Ω′ ( , , ) | .
Геометрический смысл якобиана.
Модуль якобиана равен коэффициенту искажения объемов при переходе от переменных ( , , ) к переменным ( , , ).
1.7.2. Линейная замена переменных.
Важным частным случаем замены переменных является линейная замена.

30
Рассмотрим линейное преобразование с невырожденной матрицей:
= 11 + 12 + 13 |
|
|
11 |
12 |
13 |
{ = 21 + 22 + 23 ( )=∙( ), где = ( 21 |
22 |
23), |
|||
= 31 + 32 + 33 |
|
|
31 |
32 |
33 |
= и ∆= ≠ 0.
Якобиан линейного преобразования совпадает с определителем ∆:
′ |
′ |
′ |
|
|
|
|
|
|
|
11 |
12 |
13 |
|
( , , ) = | ′ |
′ |
′ |
| = | 21 |
22 |
23 |
| = ∆. |
|
|
|
31 |
32 |
33 |
|
′ |
′ |
′ |
|
|||
|
|
|
|
|
|
|
Обратное преобразование также является линейным:
( )= −1∙( ), причем −1 = 1∆.
При линейной замене переменных тройной интеграл и объем тела (по Теореме 1.17 и Следствию 1.12) примут следующий вид:
Ω ( , , ) = |∆|∙ Ω′ ̃( , , ) , где̃( , , ) = (11 + 12 + 13, 21 + 22 + 23, 31 + 32 + 33),
(Ω) = Ω′|( , , )| = |∆|∙ Ω′ = |∆|∙(Ω′).
Впростейшем случае линейное преобразование может иметь вид:
= ∙
{ = ∙ , |
где , , = , |
≠ 0. |
|||||
= ∙ |
|
|
|
|
|
|
|
′ |
′ |
′ |
|
|
0 |
0 |
|
|
|
|
|
|
|||
Здесь ( , , ) = | ′ |
′ |
′ |
| = | |
0 |
|
0 |
| = . |
|
|
|
|
|
|||
′ |
′ |
′ |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
Следовательно, в этом случае имеем:
( , , ) = | |∙ ′ ( , , ) . |
|
|||
Ω |
Ω |
|
|
|
Пример 1.17. |
|
|
|
|
Найти объем параллелепипеда Ω, грани которого лежат в попарно параллельных |
||||
плоскостях: 1 2, 3 4, 5 6, заданных линейными уравнениями: |
||||
1: 1 + 1 + 1 = 1, |
2: 1 + 1 + 1 = 2, |
1 < 2, |
|
|
3: 2 + 2 + 2 = 1, |
4: 2 + 2 + 2 = 2, |
1 < 2, |
|
|
5: 3 + 3 + 3 = 1, |
6: 3 + 3 + 3 = 2, |
1 < 2. |
|
|
Решение. |
|
|
|
|
Параллелепипед Ω задается системой неравенств: |
|
|
|
|
1 ≤ 1 + 1 + 1 ≤ 2 |
|
1 |
1 |
1 |
{1 ≤ 2 + 2 + 2 ≤ 2 в предположении, что ∆= (2 |
2 |
2) ≠ 0. |
||
1 ≤ 3 + 3 + 3 ≤ 2 |
|
3 |
3 |
3 |
Сделаем линейную замену переменных: |
|
|
|
|
|
|||||
= 1 + 1 + 1 |
|
|
|
|
1 |
1 |
1 |
|||
{ = |
+ + |
( )=∙( ) ( )= −1∙( ), где = ( |
2 |
|
). |
|||||
2 |
2 |
2 |
|
|
|
|
|
2 |
2 |
|
= 3 + 3 + 3 |
|
|
|
|
3 |
3 |
3 |
|||
В результате такой замены новая область Ω′ задается системой неравенств:
1 ≤ ≤ 2
{1 ≤ ≤ 2 , и представляет собой прямоугольный параллелепипед с объемом:
1 ≤ ≤ 2
