Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

Все лекции

.pdf

Скачиваний:

Добавлен:

05.06.2021

Размер:

10.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 134 5 6 7 8 9 10 11 12 13 > Следующая >>>

(Ω′) = (2 − 1)∙(2 − 1)∙(2 − 1).

Якобиан линейного преобразования имеет вид:

′ ′ ′

									( , , ) = \| ′											′		′	\| = −1 =												1		.
									( , , ) = \| ′											′		′	\| = −1 =														.
																																			∆
																′				′		′													∆
																′				′		′

		Используя формулу: (Ω) = ′\|( , , )\| - найдем объем
																				Ω
параллелепипеда:
			(Ω) =					′ \|	1		\| = \|						1	\|∙(Ω′) =							1		(2 − 1)∙(2 − 1)∙(2														− 1).
			(Ω) =					′ \|			\| = \|							\|∙(Ω′) =						\|∆\|			(2 − 1)∙(2 − 1)∙(2														− 1).
							Ω		∆								∆							\|∆\|
							1																								1						1		1
Ответ:				(Ω) =			1	(				− )∙(				− )∙(					−					), где ∆= \|													\|.
Ответ:				(Ω) =				(		2		− )∙(				− )∙(					−					), где ∆= \|								2					\|.
							\|∆\|			2			1	2		1				2			1											2	2				2
							\|∆\|																								3						3		3
																															3						3		3
Пример 1.18.
																															2					2			2
		Найти объем тела, ограниченного эллипсоидом:																														+						+		= 1.
		Найти объем тела, ограниченного эллипсоидом:																													2	+				2		+	2	= 1.
Решение.
		Данное тело в декартовой системе координат задается неравенством:
2		2			2																																								= ∙
2	+	2		+	2	≤ 1. Сделаем линейную замену переменных простейшего вида: { = ∙ .

2		2			2
2		2			2																																								= ∙
																																													= ∙
Тогда получим:
			( , , ) = ,										=		, =				, =			и					2	+	2	+			2			≤ 1			2			+ 2 + 2 ≤ 1.
			( , , ) = ,										=		, =				, =			и					2	+	2	+			2			≤ 1			2			+ 2 + 2 ≤ 1.
																											2		2				2
		Это означает, что тело, ограниченное эллипсоидом в системе координат ,
переходит в единичный шар в системе координат с объемом (Ω′) =																																												4	∙13	=	4	.
																																													∙13	=		.
																																									3					3
		Используя формулу: (Ω) = ′\|( , , )\| - найдем объем эллипсоида:
																				Ω
		(Ω) = ′\| \| = \| \|∙ ′ = \| \|∙(Ω′) =																																								4	∙ .
		(Ω) = ′\| \| = \| \|∙ ′ = \| \|∙(Ω′) =																																							3		∙ .
							Ω															Ω																			3

Ответ: эллипсоида = 43 .

1.7.3. Тройной интеграл в цилиндрических и сферических координатах

Сначала рассмотрим переход от декартовой системы координат к

цилиндрической системе координатам по известным формулам:

= ∙

{ = ∙ ,

где ≥ 0,

−∞ < < + ∞,

0 ≤ < 2 или:

− < ≤ (рис. 1.29).

Вычислим якобиан перехода:

′

= ,

′

= − ∙ , ′ = 0,

′

= ,

′

∙ , ′

= 0,

′

= 0,

′

= 0,

′

= 1.

′

( , , )

= |

′

| =

′

− ∙

Рис. 1.29.

Цилиндрическая система координат

= |

∙

0| =

= \|	− ∙ \| = ∙ 2	+ ∙ 2 = ;	≥ 0	\|( , , )\| = .
	∙

Получаем тройной интеграл в цилиндрических координатах:

= ∙

( , , ) = [

= ∙

] =

′ ̃( , , ) ∙

где ̃( , , ) = ( ,

Теперь рассмотрим переход от

декартовой системы координат

к сферической системе координатам

по известным формулам (рис. 1.30):

= ∙ ∙

{ = ∙ ∙ ,

= ∙

′

где ≥ 0, 0 ≤ ≤ ,

0 ≤ < 2

(или: − < ≤ ).

Заметим, что справедливы

Рис. 1.30.

Сферическая система координат

равенства:

2 + 2 = 2∙ 2 и 2

+ 2 + 2 = 2.

Вычислим якобиан перехода:

′

= ∙ ,

′

= − ∙ ∙ ,

′

= ∙ ∙ ,

′

= ∙ ,

′

= ∙ ∙ ,

′

= ∙ ∙ ,

′

= , ′

= 0, ′

= − ∙ .

′

∙

− ∙ ∙

∙ ∙

( , , ) = | ′

′

| = | ∙

∙ ∙

∙ ∙ | =

′

− ∙

= [разложение по третьей строке] =

− ∙ ∙

∙ ∙

∙

− ∙ ∙

= | ∙ ∙

∙ ∙ | − ∙ |

∙

∙ ∙

| =

= ∙(−2 ∙ ∙ ∙ 2 − 2 ∙ ∙ ∙ 2) −

−∙ ∙( ∙ 2 ∙ 2 + ∙ 2 ∙ 2) = −2∙ ∙ 2 − 2∙ 3 =

= −2∙ ∙(2 + 2) = −2∙

|( , , )| = |−2 ∙

| = 2∙ .

Итак, имеем:

|( , , )| = 2∙

и получаем тройной интеграл в сферических

координатах:

= ∙ ∙

( , , ) = [

= ∙ ∙

= ∙

] = ′ ̃( , , ) ∙ 2

= 2

где ̃( , , ) = ( ∙ ∙ , ∙ ∙ , ∙ ).

Замечание 1.10.

Переход к сферическим координатам целесообразен в тех случаях, когда подынтегральная функция имеет вид (2 + 2 + 2), или когда область интегрирования Ω есть шар или шаровой сектор.

Пример 1.19.

Вычислить тройной интеграл:

√2+ 2+ 2 , где область Ω

задается системой неравенств:

1 ≤ 2+ 2+ 2 ≤ 4

{

≤ ≤ √3 ∙

≤ ≤

√2+ 2

√2

+ 2

√15

√3

Решение.

= √3 ∙

Область интегрирования представляет

собой пересечение трех тел:

= Ω1 ∩ Ω2 ∩ Ω3.

1) Тело Ω1 задается неравенствами:

1 ≤ 2+ 2+ 2 ≤ 4 - и представляет собой шаровой слой между двумя сферами:

2+ 2+ 2 = 1 и 2+ 2+ 2 = 4.

Рис. 1.31. Иллюстрация к Примеру 1.19

2) Тело Ω2 задается неравенствами:

≤ ≤ √3∙

ипредставляет собой двугранный угол, образованный плоскостями: = и = √3∙ , расположенными в первом октанте и проходящими через ось (рис. 1.31).

3) Тело Ω задается неравенствами:

√2+ 2 ≤ ≤

√2+ 2

- и представляет собой

√15

√3

множество, заключенное между двумя конусами: =

√2+ 2

и =

√2+ 2

√15

√3

(рис. 1.32).

√2+ 2

√3

√2+ 2

√15

Рис. 1.32.

Иллюстрация к Примеру 1.19

= ∙ ∙

Перейдем к сферическим координатам: [

= ∙ ∙

] -

= ∙

= 2

и выясним, что представляет собой область Ω′ = Ω1′ ∩ Ω2′ ∩ Ω3′ .

Ω : 1 ≤ 2+ 2+ 2 ≤ 4 1 ≤ 2 ≤ 4 Ω′ :

1 ≤ ≤ 2;

Ω2:

≤ ≤ √3∙

∙ ∙ ≤ ∙ ∙ ≤ √3∙ ∙

(т.к. > 0) Ω2′ :

;

≤ ≤ √3

1 ≤ ≤ √3

≤ ≤

∙ ≤ ∙ ≤

∙

Ω :

√2+ 2

√15

√3

√15

√3

(т.к. > 0)

≤ ≤

√3

≤ ≤ √15 Ω3′ :

≤ ≤ √15

√15

√3

1 ≤ ≤ 2

Таким образом, тело Ω′ задается системой неравенств: {

≤ ≤

- и

≤ ≤ √15

представляет собой прямоугольный параллелепипед в сферической системе координат. Следовательно, имеем:


																				3					2								√15						3
							2					2			2					3					2				3				√15						3		=
Ω √									+				+			= Ω′						=			∫1			∫ ∫													=
Ω √																= Ω′									∫1
																												4				3
																							4
	2															√15

			3 ∙∫ 3																					\|2∙ \|3∙(− )\| √15
= ∫													∙∫					=														=
= ∫													∙∫					=														=
1																3							4	1			3
1									4														4	1
									4															4
		15								1														по формуле:				] =		5	∙(		1	−		1	) =	5
=		15		∙				∙(		1	− ( √15)) = [										( ) =				1					5			1			1		5		.
=				∙				∙(			− ( √15)) = [														1															.
	4				12				2																			16				2			4			64
	4				12				2																	√1+ 2		16				2			4			64
Ответ:									=			5		.
Ответ:									=			64		.
												64
Обобщенные сферические координаты.
						При необходимости можно перейти от декартовых координат ( , , ) к
обобщенным сферическим координатам ( , , ) по следующим формулам:
																			= ∙ ∙ ∙
																			{ = ∙ ∙ ∙ ,
																						= ∙ ∙
где , , = ,																	∙ ∙ ≠ 0, ≥ 0,						0 ≤ ≤ , 0 ≤ < 2 (или:												− < ≤ ).

Такое преобразование является результатом последовательного применения двух операций: линейной замены (в простейшем случае) и перехода к сферическим координатам. Якобиан перехода в этом случае равен ( , , ) = ∙ 2∙ .

1.7.4. Приложения кратных интегралов

Рассмотрим некоторые приложения двойных и тройных интегралов.

Приложения двойного интеграла.

( ) = - площадь области .

цилиндра = ( , ) - объем цилиндрического тела Ω; тело Ω - ограничено сверху поверхностью = ( , ), снизу - областью , лежащей в плоскости и с боков - цилиндрической поверхностью с образующей, параллельной оси .

= ( , ) - масса неоднородной пластины , где ( , ) - поверхностная плотность распределения массы.

= ( , ) - электрический заряд пластины , где ( , ) - поверхностная плотность распределения заряда.

Статические моменты фигуры относительно осей координат и :

=	∙ ( , ) ,	=	∙ ( , ) .

Координаты центра тяжести (0, 0) фигуры :

=	1	∙ ,	=	1	∙ .

0			0

Моменты инерции фигуры относительно осей координат и :

=	2 ∙ ( , ) ,	=	2 ∙ ( , ) .

Момент инерции фигуры относительно точки - начала координат:

0 = (2 + 2) ∙ ( , ) = + .

Приложения тройного интеграла.

(Ω) = Ω - объем тела Ω.

= Ω (, , ) - масса неоднородного тела Ω, где (, , ) - пространственная плотность массы, распределенной по телу Ω.

= Ω (, , ) - заряд тела Ω, где (, , ) - плотность электрического заряда, распределенного по телу Ω.

Статические моменты тела Ω относительно координатных плоскостей, , и координаты центра тяжести (0, 0, 0):

= Ω ∙ (, , ) ,= Ω ∙ (, , ) ,= Ω ∙ (, , ) ;

=	1	∙ ,	=	1	∙ ,	=	1	∙ .

0			0			0

Моменты инерции тела Ω относительно осей координат , и :

= Ω (2 + 2) ∙ (, , ) ,

= Ω (2 + 2) ∙ (, , ) .

Моменты инерции тела Ω относительно координатных плоскостей

, и :

= Ω 2 ∙ (, , ) ,= Ω 2 ∙ (, , ) ,

= Ω 2 ∙ (, , ) .

Момент инерции тела Ω относительно точки - начала координат:

0 = + + .

Это лишь небольшая часть приложений кратных интегралов к задачам из геометрии, физики и механики. Конечно, есть многочисленные приложения и в других разделах естествознания и в технических дисциплинах, например, в электротехнике.

Рассмотрим одну из таких задач.

Задача (о вычислении энергии электрического поля).

Дан бесконечно длинный проводящий цилиндр, создающий электрическое поле в пространстве. Требуется найти энергию электрического поля, сосредоточенную в некотором выделенном секторе Ω, расположенном вне цилиндра.

Формула для вычисления энергии электрического поля имеет вид:

= Ω 2 ,

где Ω – выделенная область пространства, - расстояние от произвольной точки Ω до

оси цилиндра, = 82 = , – линейная плотность заряда, - диэлектрическая проницаемость среды.

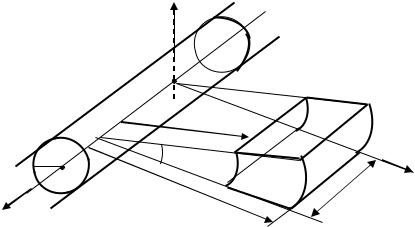
В качестве области Ω возьмем сектор, приведенный на рисунке 1.33 с указанными там «габаритами»: 1, 2, и .

		Ω
		Ω
		1

	2

Рис. 1.33. Иллюстрация к Задаче о вычислении энергии электрического поля

Решение.

Введем систему координат так, как показано на рисунке 1.33: ось направим вдоль оси цилиндра, ось - вдоль одной из боковых граней сектора Ω и так, чтобы основание сектора лежало в плоскости ; ось направим перпендикулярно осям , и так, чтобы была правая система координат.

Тогда расстояние от произвольной точки ( , , ) до оси цилиндра (оси )

				1
равно = √2 + 2, и значит, имеем:	=		= ∙		.
		2		2 + 2
	Ω		Ω

Для вычисления этого интеграла перейдем к цилиндрическим координатам:

			= ∙
	1		= ∙	1		1
∙ Ω		= [	=	] = ∙ Ω′		∙ = ∙ Ω′	,
	2+ 2				2

0 ≤ ≤

где область Ω′ задается системой неравенств: {1 ≤ ≤ 2 - и представляет собой

0 ≤ ≤

прямоугольный параллелепипед в цилиндрической системе координат. Переходя к повторным интегралам, получим:

		1					2	1								2
∙	′		= ∙∫						∙∫		∙∫			= ∙( \| 2) ∙(\|0 )∙(\|0) = ∙			.
∙	′		= ∙∫						∙∫		∙∫			= ∙( \| 2) ∙(\|0 )∙(\|0) = ∙			.
Ω						1			0			0			1
																1
									2
Ответ:				= ∙	2		=			∙		2	.
Ответ:				= ∙			=			∙			.
								82
					1							1

Глава 2. Криволинейные интегралы

В главе 1 были рассмотрены кратные интегралы. В этой главе мы остановимся на новых разновидностях интеграла: криволинейных интегралах 1 и 2 рода. Из самого названия следует, что эти интегралы рассматриваются вдоль «кривых линий».

Под «кривой линией» (или просто кривой, или просто линией) на плоскости или в пространстве подразумевается непрерывная спрямляемая кривая без самопересечений. Такие кривые будем называть простыми кривыми. Заметим, что как частный случай, кривая может быть и отрезком прямой линии.

Спрямляемость означает, что кривая имеет конечную длину (см. [4], . ). Если кривая – замкнутая, то она называется контуром.

Изучение криволинейных интегралов начнем с интегралов 1 рода.

2.1. Криволинейный интеграл 1 рода

Здесь, как и в случае кратных интегралов, сначала введем новое понятие и изучим его свойства, затем выведем формулу для вычисления и в заключение рассмотрим некоторые его приложения.

2.1.1. Понятие криволинейного интеграла 1 рода

Рассмотрим простую кривую

на плоскости или в пространстве. Пусть на этой

кривой задана некоторая функция ( ).

−2

−1

Выполним следующие действия.

Разбиение кривой на частичные дуги

точками

≡ ,

, …, ,

≡ :

−1

(рис. 2.1),

…

- дуга

(

= 1, 2, … ,

где

−1

Выбор промежуточных точек:

= 1, 2, … , .

Рис. 2.1. Разбиение кривой

Вычисление суммы:

∑

(

) ∙ ∆

где ∆

= 1, 2, … , .

= | |

- длина частичной дуги ,

Сумма

называется интегральной суммой Римана функции ( ) по кривой .

Пусть λ =

∆ - наибольшая из длин частичных дуг - ранг разбиения.

1≤ ≤

Определение 2.1.

Число называется пределом интегральных сумм при λ → 0, если для > 0

> 0 такое, что для любого разбиения кривой с рангом разбиения λ < и при

любом выборе промежуточных точек {

}

выполняется неравенство:

− |

< .

Запись:

- означает, что при λ → 0 этот предел существует, он не

λ → 0

зависит ни от способа разбиения, ни от выбора промежуточных точек, и равен числу .

Определение 2.2.

Конечный предел интегральных сумм при λ → 0 называется криволинейным интегралом 1 рода (или криволинейным интегралом по длине дуги) от функции ( ) вдоль кривой .

Обозначения: ∫

( )

или: ∫

( , ) ,

∫ ( , , ) .

Встречаются также обозначения: ∫

( ) или: ∫ ( , ) ,

∫

( , , ) .

Таким образом, по определению имеем:

∫

( ) =

∑

(

) ∙ ∆

или:

λ → 0

∫

( , ) =

∑

( , ) ∙ ∆

- для плоской кривой

λ → 0

∫

( , , ) = ∑

(

)

∙ ∆

- для пространственной кривой.

λ → 0

Функция ( ), для которой существует криволинейный интеграл 1 рода, называется интегрируемой вдоль кривой .

Пример 2.1.

	∫	0∙ =	∑=1		0∙∆		= 0 = 0	∫ 0∙ = 0;
			λ → 0				λ → 0
			λ → 0				λ → 0
∫	1∙ =	∑=1		1∙∆ =			\| \| = \| \|	∫ 1∙ = \| \| - длина кривой .
		λ → 0				λ → 0
		λ → 0				λ → 0

Физический смысл криволинейного интеграла 1 рода.

Если ( , , ) – линейная плотность массы, распределенной вдоль кривой , то

= ∫	( , , ) – масса неоднородной кривой ;
если ( , , ) – линейная плотность электрического заряда, распределенного
вдоль кривой , то
= ∫	(, , – заряд всей кривой .
	)

Замечание 2.1.

Из определения криволинейного интеграла 1 рода вытекает следующее свойство:

∫̆	( ) = ∫̆ ( ) ,

т.е. величина интеграла не зависит от направления, выбранного на кривой . Условия интегрируемости.

Сформулируем теоремы об условиях интегрируемости функции вдоль кривой. Доказательства этих утверждений аналогичны случаю кратных интегралов.

Теорема 2.1 (Необходимое условие интегрируемости).

Если функция ( ) интегрируема вдоль кривой, то она ограничена на этой кривой.

Замечание 2.2.

Обратное утверждение неверно: есть ограниченные, но не интегрируемые функции. Теорема 2.2 (Достаточное условие интегрируемости).

Пусть - гладкая кривая (см. [4], . ), а функция ( ) непрерывна на ней. Тогда эта функция интегрируема вдоль кривой .

2.1.2. Свойства криволинейного интеграла 1 рода 1. Нормированность.

Криволинейный интеграл 1 рода от единицы вдоль кривой равен длине кривой:

∫ 1∙ = | |.

2. Линейность.

Пусть функции ( ) и ( ) интегрируемы вдоль кривой . Тогда а) постоянный множитель можно выносить за знак криволинейного интеграла 1 рода:

∫ ∙( ) = ∙∫ ( ) , = ;

б) криволинейный интеграл 1 рода от суммы функций равен сумме криволинейных интегралов 1 рода от этих функций:

∫ ( ( ) + ( )) = ∫ ( ) + ∫ ( ) .

Свойство линейности можно записать в следующем виде:

∫ (1 ∙ ( ) + 2 ∙ ( )) = 1∙∫

( ) + 2∙∫

( )

1, 2 = .

3. Аддитивность.

Пусть функция ( ) интегрируема вдоль кривой . Если кривая разбита на две дуги, то криволинейный интеграл 1 рода по всей кривой равен сумме криволинейных интегралов 1 рода по каждой из этих дуг:

∫	( ) = ∫	( ) + ∫	( ) ,	где = 1 2	и 1 ∩ 2 = .
	1	2

4. Интегрирование неравенств.

Пусть функции ( ), ( ) интегрируемы вдоль кривой и удовлетворяют неравенству: ( ) ≥ ( ) . Тогда справедливо неравенство:

∫		( ) ≥ ∫	( ) .
Следствие 2.1.
а) Если ( ) ≥ 0	, то ∫		( ) ≥ 0.
б) Пусть ( ) ≥ 0		, тогда для любых дуг 1, 2 справедливо
утверждение:
1 2		∫ ( ) ≤ ∫ ( ) .
		1	2

в) |∫ ( ) | ≤ ∫ |( )|.

5. Оценки криволинейного интеграла 1 рода.

Если значения подынтегральной функции ( ) на кривой ограничены величинами и , то значение интеграла ограничено величинами ∙| | и ∙| |, где | | - длина кривой:

≤ ( ) ≤ ∙| | ≤ ∫ ( ) ≤ ∙| |

6. Теоремы о среднем значении.

Теорема 2.3.

Пусть функция ( ) интегрируема вдоль кривой и пусть

= { ( ), };					= { ( ), }.
Тогда [ ; ]:		∫	( ) = ∙\| \|,		где \| \| - длина кривой.
Число =	1	∙∫		( ) - называется интегральным средним значением функции

	\| \|
( ) на кривой .
Теорема 2.4.
Пусть функция ( ) непрерывна на кривой . Тогда 0 :
		∫		( ) = (0)∙\| \|,		где \| \| - длина кривой.

Замечание 2.3.

Доказательство всех этих свойств аналогично случаю кратных интегралов.

2.2. Вычисление криволинейного интеграла 1 рода

Покажем, как вычисление криволинейного интеграла 1 рода ∫ ( , , ) сводится к вычислению определенного интеграла.

2.2.1. Сведе́ние к определенному интегралу

̆
На кривой = введем так называемую естественную параметризацию. Это
значит, что положение произвольной точки на кривой определяется длиной дуги
̆	(рис. 2.2). Тогда кривая будет задана
= \| \|, отсчитываемой от начальной точки	(рис. 2.2). Тогда кривая будет задана
параметрическими уравнениями:
= ( )
= ( )
{ = ( ), 0 ≤ ≤ \| \|,
{ = ( ), 0 ≤ ≤ \| \|,
= ( )
где параметр (длина дуги) называется
где параметр (длина дуги) называется
естественным параметром кривой .
При этом подынтегральная функция
( , , ) сведется к сложной функции:	0

( ( ), ( ), ( )).

По определению имеем:

∫

( , , ) =

∑

( )∙∆

Рис. 2.2. Иллюстрация к естественной

λ → 0

параметризации кривой

Здесь - промежуточная точка на дуге

= (

), где

и - точки деления кривой ,

∆

−

= ∆ -

−1

= | | =

−1

Промежуточная точка

(

, , ) соответствует

длина дуги , = 1, 2, … , .

некоторому значению естественного параметра = ,

= 1, 2, … , .

Введем обозначение: ( ) = ( ( ), ( ), ( )). Тогда интегральная сумма Римана

запишется в виде:

= ∑

(

)∙∆

= ∑

( (

), (

))∙∆ =

∑

(

)∙∆ .

Следовательно, имеем:

∫

( , , ) =

∑

(

)∙∆ .

λ → 0

Если вспомнить понятие определенного интеграла (см. [4], . ), то можно

заметить, что последнее выражение есть не что иное, как определенный интеграл от

функции ( ) по промежутку [0, | |]:

∫| | ( ) =

∑

( )∙∆ .

λ → 0

Таким образом, получаем формулу:

∫

( , , ) = ∫0| | ( ) = ∫0| | ( ( ), ( ), ( ))

Полученная формула показывает, что вычисление криволинейного интеграла 1 рода сводится к вычислению определенного интеграла.

Однако эта формула имеет чисто теоретический интерес: при вычислениях она мало пригодна, так как задать конкретную кривую с помощью естественной параметризации удается крайне редко. Необходимо получить формулу для вычисления криволинейного интеграла 1 рода при произвольной параметризации кривой.

<<< < Предыдущая 1 2 34 / 134 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в папке Экзамен

#
05.06.2021154.18 Кб8Вопросы к экзамену.pdf
#
05.06.202110.65 Mб17Все лекции.pdf
#
05.06.2021101.62 Кб6Дополнительные вопросы.pdf