
|
|
= ( , ) |
|
|
|
{ |
( , ) . |
|
|
|
= ( , ) |
|
|
|
|
|
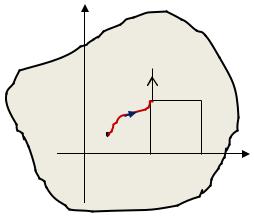
Зафиксируем некоторую внутреннюю точку0(0, 0) . Для произвольной точки ( , )
и произвольной дуги ̆ , целиком лежащей в
0
области и соединяющей точки 0 и (рис. 2.32), составим криволинейный интеграл 2 рода:
∫̆ ( , ) + ( , ) .
0
Так как этот интеграл не зависит от пути, а зависит только от точки
(при фиксированной точке 0), то он является функцией точки ( , ), т.е. функцией двух переменных ( , ). Введем обозначение:
25
2
+ ∆ 

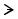
 1
1
0 |
|
|
|
|
+ ∆ |
Рис. 2.32. Иллюстрация к
доказательству Теоремы 2.9
( , ) = ∫ |
|
( , ) + ( , ) = ∫ ( , ) + ( , ) . |
|||||||||||||||||
̆ |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Докажем, что введенная таким образом функция ( , ) является искомой |
|||||||||||||||||||
функцией, т.е. для нее выполняются равенства: |
|
|
= ( , ), |
|
= ( , ). |
||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для удобства обозначим переменные интегрирования и новыми буквами и : |
|||||||||||||||||||
( , ) = ∫ |
|
( , ) + ( , ) = |
∫ ( , ) + ( , ) . |
||||||||||||||||
|
|
|
̆ |
|
|
|
|
|
|
|
|
|
|
0 |
|||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
По определению частных производных имеем: |
|||||||||||||||||||
|
|
|
|
= |
∆ |
, |
|
|
= |
|
|
∆ |
, |
||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
∆ → 0 |
∆ |
|
|
∆ → 0 |
|
∆ |
||||||||
где ∆ , ∆ - частные приращения: |
∆ = (1) − ( ) = ( + ∆ , ) − ( , ), |
||||||||||||||||||
∆ = (2) − ( ) = ( , + ∆ ) − ( , ); здесь 1( + ∆ , ), 2( , + ∆ )
(рис. 2.32).
Преобразуем частное приращение ∆ :
∆ = (1) − ( ) = ∫ 1 ( , ) + ( , ) − ∫ ( , ) + ( , ) = |
|||||
|
|
|
|
|
|
|
0 |
|
|
|
0 |
= ∫ ( , ) + ( , ) + ∫ 1 |
( , ) + ( , ) − ∫ ( , ) + ( , ) = |
||||
0 |
|
|
|
|
0 |
= ∫ 1 |
( , ) + ( , ) . |
|
|
|
|
|
|
|
|
|
|
|
Так как интеграл ∫ 1{ ( , ) + ( , )} не зависит от пути, то в качестве дуги |
||||
|
|
|
= = |
|
|
̆ |
|
|
}, параллельный оси ; тогда имеем: |
||
1 можно взять отрезок [1] = { |
+ ∆ |
||||
|
|
|
|
||
= 0 и ∆ = ∫ 1 ( , ) = |
∫+∆ ( , ) . |
|
|
||
|
|
|
|
|
|
|
Преобразуем частное приращение ∆ : |
|
|
||
∆ = (2) − ( ) = ∫ 2 ( , ) + ( , ) − ∫ ( , ) + ( , ) = |
|||||
|
0 |
|
|
|
0 |
= ∫ ( , ) + ( , ) + ∫ 2 |
( , ) + ( , ) − ∫ ( , ) + ( , ) = |
||||
0 |
|
|
|
|
0 |
= ∫ 2 |
( , ) + ( , ) . |
|
|
|
|
|
|
|
|
|
|
|
Так как интеграл ∫ 2 ( , ) + ( , ) |
не зависит от пути, то в качестве дуги |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
̆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
|
= = |
}, параллельный оси ; тогда |
||||||||||||
2 можно взять отрезок [2] = |
+ ∆ |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
имеем: = 0 и ∆ = ∫ 2 ( , ) = ∫+∆ ( , ) . |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, частные приращения равны следующим значениям: |
|
|||||||||||||||||||||||||||||||
|
|
|
|
∆ = ∫+∆ ( , ) , |
|
|
∆ = ∫+∆ |
( , ). |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По теореме о среднем для определенного интеграла имеем: |
|
|||||||||||||||||||||||||||||||
|
|
|
|
∫+∆ ( , ) = ( |
|
, )∙∆, |
|
|
+ ∆; |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ср. |
|
|
|
|
|
|
|
|
ср. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∫+∆ ( , ) = ( , |
)∙∆, |
|
|
+ ∆. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ср. |
|
|
|
|
|
|
ср. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Из непрерывности функций ( , ) и ( , ) получаем: |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
= |
|
∆ |
= |
|
( |
|
, ) = ( , ), |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
∆ → 0 ∆ |
∆ → 0 |
|
|
ср. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
= |
|
|
|
∆ |
= |
|
( , |
|
|
) = ( , ). |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
∆ → 0 |
|
∆ |
∆ → 0 |
|
|
|
ср. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Доказано, что |
|
|
|
= ( , ), |
|
= ( , ). Следовательно, ( , ) - «потенциал», а |
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
( ) - потенциальная вектор-функция в области . |
|
|
|
|
||||||||||||||||||||||||||||
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2.6.3. Условия независимости интеграла от пути |
|
||||||||||||||||||||||||||||
Предварительно докажем следующее утверждение. |
|
|
||||||||||||||||||||||||||||||
Лемма 2.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть выполнено равенство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
( , ) = |
|
( , ) для ( , ) . |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Тогда криволинейный интеграл 2 рода: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
( , ) + ( , ) - |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
не зависит от пути интегрирования в области . |
|
|
|
|
||||||||||||||||||||||||||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ввиду односвязности области любой |
|
|
|
|
||||||||||||||||||||||||||||
простой контур в ней ограничивает некоторую |
|
|
Рис. 2.33. Иллюстрация |
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
область , которая также является односвязной областью |
к доказательству Леммы 2.2 |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
(рис. 2.33). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
По формуле Грина (для односвязной области) имеем: |
|
|||||||||||||||||||||||||||||||
( , ) + ( , ) = |
|
{ |
|
( , ) − |
|
( , )} = 0 = 0, |
|
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
т.е. криволинейный интеграл по любому замкнутому контуру в области равен нулю. Согласно Лемме 2.1 это означает, что криволинейный интеграл не зависит от пути
интегрирования в области . Лемма доказана.
Теперь можно перейти к основному утверждению данного параграфа. Теорема 2.10 (условия независимости криволинейного интеграла 2 рода от пути).
Пусть - односвязная область, а функции ( , ) и ( , ) непрерывны в области
и в этой области существуют и непрерывны частные производные
( , ) и ( , ).
Тогда следующие 4 утверждения равносильны:
( ): криволинейный интеграл 2 рода ∫ ( , ) + ( , ) не зависит от пути интегрирования в области .

27
( ): криволинейный интеграл 2 рода ( , ) + ( , ) по любому замкнутому контуру в области равен нулю.
(γ): ( ) = ( ( , )) - потенциальная вектор-функция в области .
( , )
( ): |
|
( , ) = |
|
( , ) |
для ( , ) . |
|
|
|
|||||
|
|
|
|
Доказательство.
Выше были доказаны утверждения: ( ) ( ) - Лемма 2.1, ( ) (γ) - Теорема 2.9, (γ) ( ) - Замечание 2.6, ( ) ( ) - Лемма 2.2.
Имеем цепочку утверждений (импликаций): ( ) (γ) ( ) ( ), значит ( ) (γ) ( ). Следовательно, все эти 4 утверждения – действительно равносильны.
2.6.4. Обобщенная формула Ньютона-Лейбница
Если криволинейный интеграл 2 рода не зависит от пути интегрирования, то его значение на кривой равно разности потенциалов в конечной и начальной точках кривой:
∫̆ ( , ) + ( , ) = ( ) − ( ),
где ( , ) - первообразная функция подынтегрального выражения (или потенциал вектор-функции).
|
|
|
|
|
̆ |
|
|
|
|
|
= ( ) |
|
|
|
Действительно, пусть |
= - гладкая кривая: |
{ = ( ), 1 |
≤ ≤ 2 и такая, что |
|||||||||
( |
) = , |
( |
) = , |
( |
) = , |
( |
) = . Тогда имеем: |
|
|
||||
1 |
|
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
∫̆ ( , ) + ( , ) = |
∫̆ ( , ) |
= ∫ |
2 |
|
|
|
= |
||||||
|
|
{ ( ( ), ( ))} = ( ( ), ( ))| 2 |
|||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
= ( ( ), ( )) − ( ( ), ( )) = ( , |
) − ( , ) = ( ) |
− ( ). |
|
||||||||||
|
2 |
2 |
|
1 |
1 |
|
|
|
|
|
|
|
|
Полученную формулу можно назвать обобщенной формулой Ньютона-Лейбница (по аналогии с известной формулой для определенного интеграла):
∫̆ ( , ) + ( , ) = ∫̆ ( , ) = ∫ ( , ) = ( , )| = ( ) − ( ) .
Алгоритм вычисления интеграла по обобщенной формуле Ньютона-Лейбница.
Чтобы вычислить криволинейный интеграл 2 рода: ∫̆ ( , ) + ( , ) - по обобщенной формуле Ньютона-Лейбница, необходимо выполнить следующие действия.
1. Убедиться в том, что криволинейный интеграл не зависит от пути, т.е. подынтегральная функция является полным дифференциалом. Для этого следует проверить равенство:
|
( , ) = |
|
( , ) |
для ( , ) . |
|
|
|
||||
|
|
|
2. Найти первообразную функцию подынтегрального выражения (потенциал вектор-функции), т.е. составить и решить систему уравнений относительно ( , ):
{
= ( , )
.
= ( , )
3. Вычислить разность значений потенциала в конечной и начальной точках, т.е.
применить формулу: ∫̆ ( , ) + ( , ) = ( ) − ( ).
Пример 2.15.
Вычислить = ∫̆ (3 2 + 6 2) + (6 2 + 4 3) , где (1; 2), (−1, 1).

28
Решение.
1.Здесь ( , ) = 3 2 + 6 2, ( , ) = 6 2 + 4 3,
|
|
|
= (3 2 + 6 2)′ = 12 , |
|
|
|
= (6 2 + 4 3)′ = 12 , |
|||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
( , ) = |
|
( , ) |
для ( , ) 2. |
||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
Следовательно, данный криволинейный интеграл 2 рода не зависит от пути. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
= 3 2 |
+ 6 2 |
|
|
|
|
|
|
|
|
{ |
|||||
2. |
Составляем систему уравнений: |
|
. Выберем одно из этих |
|||||||||
|
|
|
|
|
|
|
|
|
|
= 6 2 |
+ 4 3 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
уравнений для его интегрирования, например, первое уравнение: |
|
||||||||||||||||
( |
, |
) |
= ∫(3 |
2 |
+ 6 |
2) |
= |
3 |
+ 3 |
2 |
|
2 |
+ |
( |
) |
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||
Подставим найденное значение ( , ) во второе уравнение: |
|
||||||||||||||||
( 3 + 3 2 2 + ( )) = 6 2 + ′ |
|
( ) = 6 2 + 4 3 ′ ( ) = 4 3 |
( ) = 4 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( , ) = 3 + 3 2 2 + 4 - первообразная функция подынтегрального выражения.
3.= ( 3 + 3 2 2 + 4)| = (−1, 1) − (1; 2) = 3 − 29 = −26.
Ответ: = −26.
Понятие потенциальной вектор-функции легко обобщается на 3-хмерный случай. Рассмотрим криволинейный интеграл 2 рода вдоль пространственной кривой :
∫ ( , , ) + ( , , ) + ( , , ) .
Определение 2.9.
( , , )
Вектор-функция ( ) = ( ( , , )) - называется потенциальной в области( , , )
3, если существует дифференцируемая в области функция ( , , ) такая, что ее полный дифференциал равен подынтегральному выражению:
( , , ) = ( , , ) + ( , , ) + ( , , ) ( , , ) .
При этом функция ( , , ) называется потенциалом вектор-функции ( ) или
первообразной для выражения ( , , ) + ( , , ) + ( , , ) .
Очевидно, что условие: ( , , ) = ( , , ) + ( , , ) + ( , , )( , , ) - равносильно системе дифференциальных уравнений в частных
= ( , , )
производных: = ( , , ).
{ = ( , , )
Здесь также имеет место обобщенная формула Ньютона-Лейбница:
∫̆ ( , , ) + ( , , ) + ( , , ) = ∫̆ ( , , ) = ∫ ( , , ) = = ( , , )| = ( ) − ( ) = ( , , ) − ( , , ).
Из этой формулы следует, что в случае потенциальной вектор-функции криволинейный интеграл 2 рода вдоль пространственной кривой также не зависит от пути, а зависит только от его начала и конца.
Общие условия независимости криволинейного интеграла 2 рода вдоль пространственной кривой будут обсуждаться далее в главе 4 «Элементы теории поля».
29
Пример 2.16.
|
|
|
|
|
|
Вычислить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
а) |
= ∫ |
|
|
|
+ 32 − 23 , где |
(2; 1; 0), (4; −1; 2); |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
̆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
б) |
= ∫̆ |
|
+ + , где |
(4; 1; 1), (1; 2; 3). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
а) = ∫̆ + 32 − 23 = ∫̆ |
|
( |
2 |
) + (3) − ( |
4 |
) = ∫̆ |
( |
2 |
+ 3 − |
4 |
) = |
|||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
2 |
|
||||||||||||
|
= ( |
2 |
+ 3 − |
|
4 |
) | = (8 − 1 − 8) − (2 + 1 − 0) = −4. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
б) = ∫ |
+ + = ∫ |
( ) = ( )| = 1∙2∙3 − 4∙1∙1 = 6 − 4 = 2. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
̆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: а) = −4; |
|
|
б) = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Приложения криволинейных интегралов 2 рода. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Площадь плоской фигуры: ( ) = |
1 |
∙ |
|
( − ). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Работа силы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
по перемещению материальной точки вдоль кривой : |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
= ∫ |
|
|
|
|
|
|
|
|
|
(, ) + (, ) - для плоской кривой; |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
( ) ∙ = ∫ |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
= ∫ |
|
|
|
|
|
|
|
|
|
(, , ) + (, , ) + (, , ) - для |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
( ) ∙ = ∫ |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
пространственной кривой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Пример 2.17. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
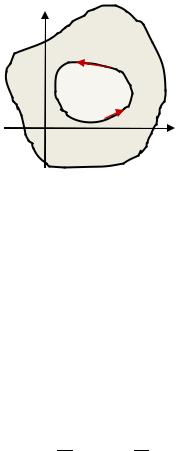
Найти площадь фигуры, ограниченной астроидой: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
= ∙ 3 |
(рис. 2.34). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∙ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Вычислим площадь по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
1 |
∙ ( − ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
При обходе фигуры вдоль кривой |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.34. К Примеру 2.17 |
|||||||||||||||||||||||||||||||||||||||
в положительном направлении параметр |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
изменяется от 0 до 2. Следовательно, имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
= |
1 |
∙ |
|
( − ) = |
1 |
∙∫2 {3 ∙ 32 |
∙ + 3 ∙ 32 ∙ } = |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
1 |
∙32 |
∫2 (4 ∙ 2 + 4 ∙ 2) = |
|
1 |
∙32 |
∫2 2 ∙ 2 = |
|||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
1 |
∙32 |
∫2 |
1 |
|
∙ 22 = |
1 |
∙32 |
∫2 |
1− 4 |
= |
1 |
∙32 ( − |
1 |
|
4 ) |02 |
= |
3 2 |
. |
|||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
16 |
4 |
|
|
|
|
|
8 |
|
|
|
|||||||||||||
Ответ: |
|
= |
3 2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2.18. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
Найти работу силы |
|
|
|
|
6 |
∙ + ∙ |
вдоль кривой = |
3 |
от точки (0; 0) до |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
= 4 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
точки (1; 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
Вычислим работу по формуле: = ∫ |
|
|
|
(, ) + (, ) . |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
( ) ∙ = ∫ |
|||||||||||||||||||||||||||||||||||||||||||||||||||
В нашем случае получим:
= ∫ (46 ∙ + ∙ ) = ∫01(46 ∙ + ∙ 3 ∙ 32 ∙ ) = ∫01 76 = 7|10 = 1.
Ответ: = 1.
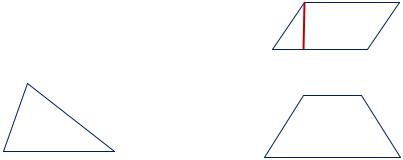
Глава 3. Поверхностные интегралы
Данная глава посвящена еще двум разновидностям интеграла: поверхностным интегралам 1 и 2 рода. Эти интегралы рассматриваются на участках «кривых поверхностей» или плоскостей. Изучение поверхностных интегралов начнем с понятия площади кривой поверхности.
3.1.Площадь кривой поверхности
Впредыдущих главах мы неоднократно использовали понятия площади и объема, не углубляясь особо в их смысл, а лишь ограничиваясь интуитивными представлениями о них. Здесь мы уточним эти понятия и рассмотрим их свойства.
3.1.1.Понятие площади плоской фигуры
Пусть – некоторая фигура (не обязательно область) на плоскости. Если для этой фигуры определено понятие площади, то фигура называется квадрируемой, а ее площадь обозначается как ( ).
Заметим сразу, что не любая фигура на плоскости будет квадрируемой, т.е. не всякая фигура имеет площадь. Однако все известные из элементарной геометрии фигуры будут квадрируемы.
Введем понятие площади аксиоматическим путем.
Определение 3.1.
Площадью называется неотрицательная функция, заданная на множестве квадрируемых фигур на плоскости, принимающая значение 0 для пустого множества, значение 1 для единичного квадрата, обладающая свойством аддитивности и сохраняющая свое значение при движении фигур:
1.( ) = 0, (□) = 1;
2.если 1 ∩ 2 = , то ( 1 2) = ( 1) + ( 2);
3.если 1 и 2 - конгруэнтны (равны), то ( 1) = ( 2).
Конгруэнтными называются такие фигуры, которые могут быть совмещены друг с другом с помощью некоторого движения (параллельного переноса, поворота и т.д.).
Очевидно, что свойство аддитивности можно обобщить на любое конечное число
«слагаемых»: |
|
|
|
|
|
|
|
|
|
|||
|
|
если = |
, где |
∩ = ( ≠ ), то |
( ) = ∑ |
( ). |
||||||
|
|
|
=1 |
|
|
=1 |
|
|
||||
|
Как следствие этих аксиом получаем формулы для площадей прямоугольника, |
|||||||||||
параллелограмма, треугольника и трапеции (рис. 3.1): |
|
|
|
|||||||||
|
|
|
|
= ∙ |
|
|
= ∙ |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
= |
1 |
∙ |
|
|
= |
1 |
( + ) ∙ |
||
|
|
|||||||||||
|
|
|
|
|||||||||
|
|
|
|
|||||||||
|
|
|
|
2 |
||||||||
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.1. Формулы для площадей некоторых геометрических фигур
Если фигуру можно разбить на конечное число частей указанного вида, то ее площадь вычисляется как сумма площадей этих частичных фигур. Например,
2
площадь многоугольника равна сумме площадей |
|
|
|
|
|
|
|
|
|
||
треугольников, из которых состоит этот |
|
|
1 |
|
|
многоугольник (рис. 3.2). |
|
|
|
||
|
|
|
|
||
|
|
|
|||
Далее, используя аксиомы 1, 2 и 3, |
|
|
|
||
|
|
|
|
||
можно распространить понятие площади |
|
|
2 |
|
|
для произвольных фигур на плоскости. |
|
|
4 |
|
|
Пусть - фигура на плоскости, |
|
|
3 |
|
|
|
|
|
|
||
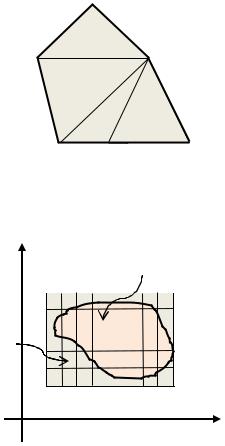
ограниченная замкнутым контуром. Поместим |
|
|
|
|
|
|
|
|
|||
фигуру в прямоугольник П, стороны которого |
Рис. 3.2. Площадь многоугольника |
||||
параллельны осям координат (рис. 3.3). |
|||||
|
|
|
|
||
Разобьем прямоугольник П на частичные прямоугольники прямыми, |
|
||||
параллельными осям координат |
|
|
|
|
|
Эти частичные прямоугольники можно |
|
|
|
|
|
разделить на три группы: |
|
|
|
|
|
1) все те, которые целиком лежат внутри фигуры ; |
|
|
|
||
|
|
|
|||
2) все те, которые имеют общие точки как с самой |
|
|
… |
|
|
|
П |
|
|
||
фигурой , так и с ее внешней частью; |
|
|
|
||
3)все остальные, т.е. те, которые целиком лежат вне фигуры .
Введем обозначения:
− - сумма площадей всех частичных |
|
|
|
|
прямоугольников из 1-й группы; |
|
Рис. 3.3. Иллюстрация к |
||
+ - сумма площадей всех частичных |
|
|||
|
понятию площади фигуры |
|||
прямоугольников, входящих в 1-ю и 2-ю группы. |
||||
|
|
|||
Суммы + и − зависят от способа разбиения прямоугольника П, но при этом |
||||
− ≤ + при любом способе разбиения. |
|
|
||
Пусть λ - ранг разбиения, т.е. λ = {1, … , }, где |
– длина диагонали |
|||
частичного - го прямоугольника, = 1, 2, … , . |
|
|
||
Определение 3.2. |
|
|
|
|
Если существуют пределы +, −, не зависящие от способа разбиения |
||||
λ → 0 |
λ → 0 |
|
|
|
фигуры , и они совпадают: + = |
− = , то этот общий предел называется |
|||
λ → 0 |
λ → 0 |
|
|
|
площадью фигуры , а сама фигура называется квадрируемой. Справедливо следующее утверждение.
Теорема 3.1.
Для того чтобы фигура была квадрируемой, необходимо и достаточно, чтобы выполнялось равенство:
(+ − −) = 0.
λ→ 0
Ввопросе квадрируемости фигуры существенную роль играет контур,
ограничивающий данную фигуру.
Теорема 3.2.
Пусть фигура ограничена замкнутым контуром . Для того чтобы фигура была квадрируемой, необходимо и достаточно, чтобы контур имел площадь, равную нулю.
3
Доказательство этих теорем можно найти в работах [1] и [2]. В этих работах указан широкий класс кривых, имеющих нулевую площадь. К этому классу кривых с нулевой площадью, в частности, относятся:
- любая непрерывная кривая , заданная в декартовой системе координат явным уравнением:
= ( ), [ ; ] или = ( ), [ ; ]; - любая кусочно-гладкая кривая , заданная параметрическими уравнениями:
= ( )
{ = ( ), [ ; ] и т.д.
Таким образом, все известные нам кривые имеют нулевую площадь, а фигуры, ограниченные ими, являются квадрируемыми, т.е. они имеют площадь.
Тем не менее, существуют кривые и с ненулевой площадью и соответственно, неквадрируемые фигуры.
3.1.2. Связь между площадью плоской фигуры и площадью ее проекции
В дальнейшем нам понадобится следующее свойство, связанное с площадями фигур, расположенных в разных плоскостях пространства.
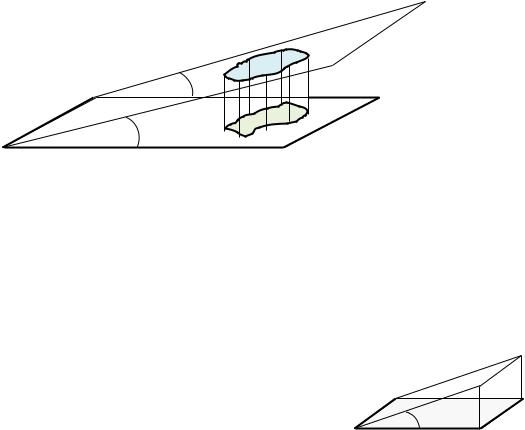
Пусть имеются две плоскости и ′ с двугранным углом между ними < 90°, фигуры , ′ ′, причем является проекцией ′ на плоскость (рис. 3.4).
Найдем связь между площадями ( ) и (′).
′
|
′ |
|
|
|
|
|
|
|
Рис. 3.4. Изображение проекции плоской фигуры
Площадь фигуры ′ есть по определению предел суммы площадей частичных
прямоугольников: (′) = + = |
−. Сначала найдем связь между площадью |
|||||||
|
λ → 0 |
λ → 0 |
|
|
|
|
|
|
прямоугольника, лежащего в плоскости ′ и площадью соответствующего (при |
||||||||
проектировании) прямоугольника, лежащего в плоскости . |
|
|
|
|
||||
При проекции прямоугольника на плоскость |
одна из его сторон сохраняет |
|||||||
свою длину, а другая сторона ′ примет значение , равное |
′ (рис. 3.5). |
|||||||
Следовательно, имеем: |
|
|
|
|
|
′ |
||
= ∙ = ∙ ′ γ = ′∙ γ. |
|
|
|
|||||
Так как это соотношение между площадями верно |
|
|
|
|
||||
для всех частичных прямоугольников, то оно верно и |
|
|
||||||
|
|
|||||||
для сумм этих площадей и для пределов этих сумм. |
|
|
|
|||||
|
|
|
|
|
|
|||
В результате получим: |
|
|
|
Рис. 3.5. Изображение |
||||
|
|
|
|
|
||||
|
( ) = (′) ∙ γ |
. |
прямоугольника и его проекции |
|||||
Замечание 3.1.
Понятие объема пространственной фигуры вводится по схеме, аналогичной
4
рассмотренной выше схеме для площади плоской фигуры. Останавливаться подробно на этом мы не будем. Отметим лишь то, что встретится в дальнейшем изложении, а именно: объем любой (практически) поверхности (как и площадь любой кривой), равен нулю.
Перейдем к рассмотрению некоторых дополнительных сведений из геометрии.
3.1.3. Касательная прямая и нормальная плоскость к пространственной кривой
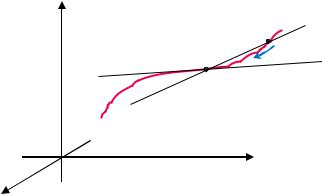
Пусть имеется пространственная кривая и точка 0 . Проведем секущую через точку 0 и некую другую точку на этой кривой (рис. 3.6).
Определение 3.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Касательной (прямой) в точке 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
к пространственной кривой называется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
предельное положение секущей, проходящей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||||||||||||||||
через точку 0 и некую другую точку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
на этой кривой, когда точка вдоль |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
этой кривой стремится к точке 0 (рис. 3.6). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Составим уравнения этой касательной. |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Пусть кривая задана |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
параметрическими уравнениями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.6. Иллюстрация к понятию |
||||||||||||
{ = ( ), [ ; ], |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
касательной прямой |
|||||||||||||
= ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где ( ), ( ), ( ) - непрерывно-дифференцируемые функции, |
0(0, 0, 0) , |
||||||||||||||||||||||||||||||||||
0 = (0), 0 = (0), |
0 = (0), |
0 [ ; ]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Возьмем текущую точку (0 |
+ ∆ , 0 + ∆ , 0 + ∆ ) . |
Тогда уравнения |
|||||||||||||||||||||||||||||||||
секущей [ ] будут иметь вид: |
|
− 0 |
= |
− 0 |
|
= |
− 0 |
. |
Разделим знаменатели этих |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
∆ |
|
|
|
|
∆ |
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
− |
|
− |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
дробей на величину ∆: |
|
0 |
= |
|
|
|
0 |
|
= |
|
|
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
∆ |
|
|
∆ |
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
∆ |
|
|
∆ |
|
|
|
|
|
|
∆ |
|
|
− 0 |
|
|
|
|
− 0 |
|
|
− 0 |
|
|||||||||||
Переходя к пределу при ∆ → 0, получим: |
|
|
= |
|
|
= |
|
. |
|||||||||||||||||||||||||||
|
|
′( ) |
|
|
′( ) |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′( ) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|||||
Таким образом, имеем уравнения касательной: |
|
− 0 |
|
= |
|
− 0 |
|
= |
− 0 |
|
. |
||||||||||||||||||||||||
|
′( ) |
|
′( ) |
′( ) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|||||
Вектор {′( ), ′( ), ′( )} |
является направляющим вектором касательной к |
||||||||||||||||||||||||||||||||||
0 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
кривой в точке 0(0, 0, 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Замечание 3.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения касательной теряют смысл, если ′( |
) = ′( |
|
) |
= ′( ) = 0. В этом |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
0 |
||||
случае точка 0(0, 0, 0) называется особой точкой кривой . В особых точках кривой касательная не существует.
Если же хотя бы одна из координат вектора {′(0), ′(0), ′(0)} отлична от нуля, то точка 0(0, 0, 0) называется обыкновенной точкой кривой . В обыкновенных точках кривой касательная существует, и она единственна.
Определение 3.4.
Нормальной плоскостью кривой в точке 0 называется плоскость, проходящая через точку 0 перпендикулярно касательной к этой кривой в данной точке (рис. 3.7).
Направляющий вектор касательной к кривой в точке 0 перпендикулярен нормальной плоскости в данной точке. Следовательно, уравнение нормальной плоскости имеет вид:
5
|
|
|
|
|
′( |
|
) ∙ |
( − |
|
) + ′( |
) ∙ ( − |
) + ′( |
|
) ∙ ( − ) = 0 |
. |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
0 |
0 |
|
0 |
|
|
|
|
||||||
Пример 3.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Составить уравнения касательной |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
прямой и нормальной плоскости к кривой , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||
где : { = |
2 |
- в точке, соответствующей |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
= |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
параметру 0 = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
||
( 0) = 1, ( 0) = 1, |
|
|
( 0) = 1 0(1, 1, 1); |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
′( ) = 1, ′( ) = 2, ′( |
|
|
) |
= 3 {1; 2; 3}. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Уравнения касательной прямой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
− 1 |
= |
|
|
− 1 |
= |
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.7. Нормальная плоскость |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
3 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кривой в точке |
|
|||||||||||||||||||
Уравнение нормальной плоскости: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
1∙( − 1) + 2∙( − 1) + 3∙( − 1) = 0 + 2 + 3 − 6 = 0. |
|
||||||||||||||||||||||||||||||||||||||||||||
Ответ: |
− |
1 |
= |
− |
1 |
= |
− |
1 |
; |
|
|
+ 2 + 3 − 6 = 0. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
1 |
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
3.1.4. Касательная плоскость и нормаль к поверхности в пространстве |
|
||||||||||||||||||||||||||||||||||||||||||||
Рассмотрим в пространстве 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
поверхность , заданную уравнением: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( , , ) = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
где функция ( , , ) дифференцируема |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||||||||||||||||||||||
в окрестности точки 0( 0, 0, 0) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Рассмотрим всевозможные гладкие кривые , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
лежащие на поверхности и проходящие |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
через точку 0 (рис. 3.8): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
||||||||||||||||
= ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
: { = ( ), [ ; ], |
|
( 0, 0, 0) = 0, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
= ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.8. Изображение касательной |
||||||||||||
0 = ( 0), 0 = ( 0), 0 = ( 0), |
0 [ ; ]; |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
плоскости к поверхности в точке |
|||||||||||||||||||||||||||||||||||||||||||
( ( ), ( ), ( )) = 0 [ ; ]. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Продифференцируем равенство: ( ( ), ( ), ( )) = 0 |
на промежутке [ ; ]. |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ ( ( ), ( ), ( ))} = 0 [ ; ] |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
′ ( ( ), ( ), ( ))∙ |
|
|
+ ′ |
|
( ( ), ( ), ( ))∙ |
|
|
+ ′ ( ( ), ( ), ( ))∙ |
|
= 0 [ ; ]. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Подставим в это равенство значение = 0: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
′ ( |
, , |
)∙ |
′( ) |
+ ′ ( |
, , |
|
|
)∙ ′( |
|
) + ′ ( |
|
, , |
)∙ ′( ) = 0, или |
|
|||||||||||||||||||||||||||||||
0 0 0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 0 0 |
|
|
0 |
|
0 |
0 0 |
0 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
′ ( |
|
)∙ ′( |
|
) + ′ |
( |
)∙ ′( |
) |
+ ′ |
( )∙ ′( ) |
= 0. |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|||||
Определение 3.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Вектор |
|
|
|
′ |
( ), |
′ |
|
|
|
|
′ |
( |
|
)} с координатами из частных производных |
|||||||||||||||||||||||||||||||
{ |
|
|
|
|
( ), |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
функции ( , , ) в точке 0 - называется градиентом функции ( , , ) в точке 0. |
|||||||||||||||||||||||||||||||||||||||||||||
Так как вектор { ′( |
|
), ′( ), ′ |
( )} |
– это направляющий вектор касательной к |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кривой в точке 0, то полученное при дифференцировании равенство можно записать в виде равенства нулю скалярного произведения двух векторов:
