Все лекции

Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

Следствие 4.4.

.pdf

Скачиваний:

Добавлен:

05.06.2021

Размер:

10.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1312 13 > Следующая >>>

		γ

( ) = |

| = ∙|

Частный случай формулы Стокса.

Если взять контур в плоскости ( = 0), а в качестве поверхности , натянутой на этот контур, выбрать область , ограниченную этим контуром, то из формулы Стокса получим формулу Грина:

( + ) = ( − ) .

Следовательно, формула Грина (см. п. 2.5.2) есть частный случай формулы Стокса, а формула Стокса является обобщением формулы Грина на случай пространственного контура.

4.3.3. Ротор векторного поля
Введем понятие ротора векторного поля
	( , , ) .
( ) = ( , , )∙ + ( , , )∙ + ( , , )∙ ,	( , , ) .
Определение 4.13.

Ротором (вихрем) векторного поля называется вектор следующего вида:

= \|

| = (

−

) + (

−

) + (

−

) .

Пример 4.14.

Найти , где = 3∙ + 3∙ + 3∙ .

Решение.



						(3)			(3)		(3)			(3)			(3)		(3)
= \|					\| = (			−		) − (			−			) + (		−		) =
= \|					\| = (			−		) − (			−			) + (		−		) =
	3	3	3
= (0 − 0) − (3				2	2							2		2	) .
= (0 − 0) − (3					− 3		) + (0 − 0) = 3(						−		) .

Ответ: = 3( 2 − 2) .

Если ( ) = , где { , , } - радиус-вектор точки , то имеем:

= |

| = (

−

) − (

−

) + (

−

) = 0∙ − 0∙ + 0∙ = 0.

Значит, ротор радиус-вектора точки равен нулевому вектору. Замечание 4.6.

Для плоского векторного поля ( ) = ( , )∙ + ( , )∙ имеем:

= |

| = (

−

) .

(, )

(, ) 0

Используя оператор Гамильтона: =

∙ +

∙ - можно записать ротор

векторного поля в виде векторного произведения векторов:

= × .

Тогда функция ( ) из формулы Стокса равна скалярному произведению векторов:

( ) = 0∙ = ∙ 0,

а поверхностный интеграл 1 рода равен потоку П вектора через поверхность :

( ) = ( ∙ 0) = П.

Следовательно, теорема Стокса имеет следующую (векторную) формулировку.

Циркуляция векторного поля ( ) по замкнутому контуру равна потоку ротора этого векторного поля через любую поверхность , натянутую на контур :

	( ∙ 0)	- формула Стокса.
( ∙ ) =

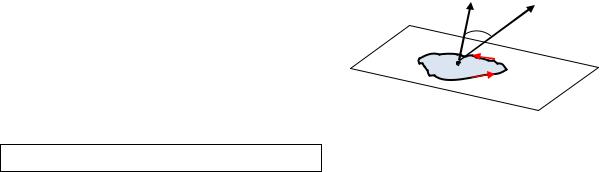
Выясним связь между понятиями плотность циркуляции ( ) и ротор ( ) в данной точке.

Применяя формулу Стокса для плоского контура и теорему о среднем для поверхностного интеграла 1 рода (см. п. 3.2.2), а также непрерывность функции ( ), получим:

			( ) = (ср)∙ (D)
	( ∙ ) =		( ) = (ср)∙ (D)

		( ) =	1
		( ) =		(D)	∙ ( ∙ ) =
		{ } →		(D)
=		(ср) = ( ) = ( )∙ 0( ).
	{ } →
						и
		Учитывая, что векторы 0( )				и

| 0| = 1, получим:

( ) = | ( )| ∙ = Пр ( ) ,








Рис. 4.21. Угол между
векторами
векторами	и нормали

где - угол между векторами ( ) и (рис. 4.21).

Таким образом, плотность циркуляции в точке равна проекции ротора на вектор нормали в этой точке.

Полученная формула выражает зависимость плотности циркуляции от направления вектора . Эта зависимость выражается наличием множителя , а величина | | от вектора не зависит.

Свойства ротора.

1. Ротор направлен в сторону наибольшего значения плотности циркуляции.

Это следует из формулы: ( ) = | ( )|∙ . Наибольшее значение плотности ( ) достигается при = 0, т.е. при условии, что .

2. Модуль ротора равен наибольшему значению плотности циркуляции в данной

точке.

Действительно, имеем: {

( )} = {| ( )| ∙ } = | ( )|.

3. Дивергенция ротора равна нулю: ( ( )) = 0.

Действительно, имеем: = (

−

) + (

−

) + (

−

)

( ( )) =

(

−

) +

(

−

) +

(

−

) =

= (

−

) + (

−

) + (

−

) =

= (	2	−	2	) + (	2	−	2	) + (	2	−	2	) = 0 + 0 + 0 = 0.

Замечание 4.7.

Из свойств 1 и 2 следует, что не зависит от выбора системы координат, хотя в определении ротора (Определение 4.13) и присутствует система координат . Эта независимость вытекает из того, что ротор непосредственно связан с плотностью циркуляции, которая определяется без привязки к системе координат (Определение 4.12).

Физический смысл ротора.

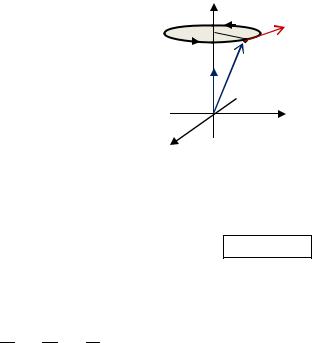
Найдем ротор поля линейных скоростей твердого тела, вращающегося вокруг оси

с постоянной угловой скоростью (рис. 4.22).

Поле линейных скоростей задается формулой

(см. п. 4.2.1): = − ∙ + ∙ . Вычислим ротор

этого поля: = |

| =

−

(0)

( )

(0)

(− )

( )

(− )

= (

−

) − (

−

) + (

−

) = Рис. 4.22. Иллюстрация к

физическому смыслу ротора

= (0 − 0) − (0 − 0) + ( + ) = 2 = 2.

Таким образом, ротор поля линейных скоростей вращающегося твердого тела

одинаков во всех точках этого тела и равен удвоенной угловой скорости: = 2 . С этим физическим смыслом и связано название «ротор» («вращатель», вихрь).

Правила вычисления ротора.

Ротор векторного поля , как показано выше, равен векторному произведению векторов и : = × , где = ∙ + ∙ + ∙ - оператор Гамильтона.

Таким образом, ротор - это оператор, преобразующий одну векторную величину в другую векторную величину и определяемый равенством: = × .

Отметим следующие правила вычисления ротора.

(1)= 0 , где = .

(2)( ∙ ) = ∙ , где = .

(3)( 1 + 2) = 1 + 2.

(4)( ∙ ) = ∙ + × = ∙( × ) + × ,

где - скалярная функция,

- градиент .

Эти правила легко проверяются, если использовать формулу: = × .

Докажем, например, правило (4): ( ∙ ) = × ( ∙ ) = |

| =

∙

( ∙ )

= (

−

) − (

−

) + (

−

) =

= ∙{(

−

) − (

−

) + (

−

) } +

+ {(

∙ −

∙ ) − (

∙ −

∙ ) + (

∙ −

∙ ) } =




= ∙ + \|						\| = ∙ + × .
= ∙ + \|						\| = ∙ + × .

Замечание 4.8.

Правила (2) и (3) означают, что ротор - это линейный оператор.

Ротор центрального векторного поля.

Пример 4.15.

Найти ротор центрального векторного поля ( ) = ( )∙ , где { , , } –

радиус-вектор точки , = | | = √2 + 2 + 2.

Решение.

По Правилу 4 имеем:

( ( )

∙ ) = ( )∙ + ( ) × .

′

Так как = 0 и

( ) =

( )∙ (см. Пример 4.6), то получим:

( ( ) ∙ ) = ( )∙0 + ′( )∙

× = 0 +

′( )

∙( × ) = 0 +

′( )

∙0 = 0.

Ответ: ротор центрального векторного поля равен нулевому вектору: ( ( ) ∙ ) = 0.

Безвихревые векторные поля.

Определение 4.14.

Векторное поле называется безвихревым, если ротор этого поля в каждой точке равен нулевому вектору:

{ = ( ), } – безвихревое поле ( ) = 0 .

Например, центральное поле ( ) = ( )∙ - безвихревое поле, так как

( ( ) ∙ ) = 0 (см. Пример 4.15).

Другими словами, все центральные векторные поля – безвихревые поля. Еще одним примером безвихревого поля является поле градиентов: = .

Действительно, имеем:

(′)

(′ )

(′)

(′ )

= ( ) = |

| = (

−

) − (

−

) + (

−

) =

′

= (

−

) − (

−

) + (

−

) = 0∙ − 0∙ + 0∙ = 0.

Таким образом, получаем важное равенство: () = 0 .

Из определения ротора (Определение 4.13) вытекают условия, при которых векторное поле будет безвихревым:

	−	= 0	=


( ) = 0	−	= 0		=	( , , ) .

{

−

= 0

{

Для плоского векторного поля ( ) = ( , )∙ + ( , )∙

безвихревое поле

определяется условием:

−

= 0

( , ) , или:

( ) = ( , )∙ + ( , )∙ -

безвихревое поле

( , ) .

4.4. Специальные векторные поля

Рассмотрим векторные поля, обладающие некоторыми специальными свойствами.

4.4.1. Потенциальные поля

Определение 4.15.

Векторное поле { = ( ), } - называется потенциальным, если существует

такое скалярное поле = ( ), , градиент которого совпадает с вектором ( ) в любой точке области :

( ) = ( ) .

Другими словами, потенциальное поле – это поле градиентов.

Если ( ) = ( , , )∙ + ( , , )∙ + ( , , )∙ , то потенциальность этого поля означает существование скалярной функции (потенциала) ( , , ), для которой выполняются следующие равенства:

= ( , , )

= ( , , ) ( , , ) = ( , , ) + ( , , ) + ( , , ) ( , , ) .

{ = ( , , )

Замечание 4.9.

Потенциал векторного поля определяется с точностью до постоянного слагаемого:

если ( ) – потенциал

( ), то ( ) + ,

где = , - также потенциал.

В потенциальном поле линейный интеграл ∫

от векторного поля ( )

( )∙

равен разности значений потенциала ( ) в конечной и начальной

вдоль кривой =

точке кривой (см. п. 2.6.4):

∫

(, , ) = (, , )|

= ( ) − ( ) = (

, )

− ( , , )

( ∙ ) = ∫

Примеры потенциальных полей.

1. Поле Ньютоновского притяжения:

( ) = −

∙

= −

∙

= −

∙ ,

где = | | = √2

+ 2

+ 2,

{ , , } - радиус-вектор точки ,

- сила притяжения.

′

В Примере 4.6

была получена формула: ( ) =

( )∙

( )∙ 0.

′

( )∙ 0

= ( ). Следовательно,

Если взять =

, то получим:

= −

∙ 0

( ) - потенциальное поле с потенциалом =

2. Электростатическое поле точечного заряда:

( ) =

∙

∙ 0

∙ ,

где

= | | = √

{ , , } - радиус-вектор точки

– электрическая

напряженность.

Здесь ( ) = , где = − ; следовательно, ( ) - потенциальное поле

с потенциалом = − .

Замечание 4.10.

В обоих приведенных выше примерах поля являются центральными полями. Далее нам потребуется понятие односвязной области в пространстве 3.

Определение 4.16.

Область 3 называется односвязной (поверхностно односвязной), если на любой замкнутый контур, лежащий в этой области, можно натянуть поверхность, целиком лежащую в области .

Примеры односвязных областей: все пространство 3; внутренность сферы; внутренность параллелепипеда; и т.д.

Примеры неодносвязных областей: внутренность тора; пространство 3, из которого удалена прямая; и т.д.

Рассмотрим векторное поле: ( ) = ( , , )∙ + ( , , )∙ + ( , , )∙ , ( , , ) , где - односвязная область, а функции ( , , ), ( , , ), ( , , )

непрерывны вместе со своими частными производными 1- го порядка в области .


Пусть ( ) = ∫ ( ∙ ) = ∫ { (, , ) + (, , ) + (, , ) } -

линейный интеграл от векторного поля ( ) вдоль кривой , ;
	векторного поля ( ) вдоль замкнутого контура.
Ц = ( ∙ ) - циркуляция
Основные свойства потенциального поля.
Основные свойства потенциального поля вытекают из следующей теоремы.
Теорема 4.4.
Следующие утверждения равносильны:
( ): линейный интеграл ( ) не зависит от пути интегрирования в области .

( ): циркуляция по любому замкнутому контуру в области равна нулю: Ц = 0. (γ): поле ( ) - потенциальное поле в области .

( ): поле ( ) - безвихревое поле: ( ) = 0 .

Доказательство.

Утверждения: ( ) ( ) и ( ) (γ) – доказываются аналогично случаю потенциальной вектор-функции ( ), заданной на плоскости 2 (см. п. 2.6.1 и 2.6.2).

Утверждение (γ) ( ):		(см. п. 4.3.3).
	( ) = () = 0
Утверждение ( ) ( ):			( ∙ 0) =
	Ц = ( ∙ ) = [формула Стокса] =

(0 ∙ 0) = 0. Теорема доказана.

Таким образом, в потенциальном поле с односвязной областью циркуляция по любому замкнутому контуру равна нулю, а линейный интеграл не зависит от пути интегрирования и равен разности потенциалов в конечной и начальной точке кривой.

Кроме того, это потенциальное поле является безвихревым, т.е. ротор векторного поля в каждой точке равен нулю (нулевому вектору).

Замечание 4.11.

Для плоского векторного поля: ( ) = ( , )∙ + ( , )∙ - эта теорема идентична теореме о независимости криволинейного интеграла 2 рода от пути на плоскости (см. п. 2.6.3). При этом безвихревое поле определяется условием:

Все центральные векторные поля, заданные в односвязной области - потенциальны. Это вытекает из равенства: ( ) = ( ( ) ∙ ) = 0 (см. Пример 4.15).

Пример 4.16.

Вычислить линейный интеграл ( ) от векторного поля = 2∙ + 2∙ + 2∙ вдоль произвольной кривой , соединяющей точки (−1; 0; 2) и (−2; 1; −1).

Решение.

Сначала докажем потенциальность этого поля. Согласно Теореме 4.4 для этого достаточно показать, что поле – безвихревое.



					(2)		(2)		(2)		(2)		(2)		(2)
= \|				\| = (		−		) − (		−		) + (		−		) =
	2	2	2

= (0 − 0) − (0 − 0) + (0 − 0) = 0. Поле - безвихревое,

Найдем потенциал этого поля:

( , , ) = 2 + 2 + 2 = 13 ( 3) + 13 ( 3) + 13

значит, оно потенциальное.

( 3) = ( 3+ 3+ 3)

( , , ) =

3+ 3+ 3

. Следовательно, имеем:

( ) = ∫̆

( , , ) = (

3+ 3+ 3

) | =

−8 + 1 − 1

−

−1+ 0 + 8

= −5.

Ответ: ( ) = −5.

Пример 4.17.

Найти потенциал векторного поля: ( ) = ∙ ,

где = | | = √ 2 + 2 + 2,

{ , , } - радиус-вектор точки .

Решение.

( ) - центральное поле, значит оно потенциальное. Для нахождения потенциаласоставим систему уравнений:

			= ∙
	∙

( ) = ∙( ) = ( ∙ )			= ∙ .

	∙
			= ∙
		{

Для решения этой системы выбираем одно из уравнений и проинтегрируем его по той же переменной, по которой вычисляется частная производная, например:

( , , ) = ∫

= ∫ ∙ = ∫ √ 2 + 2 + 2 ∙ =

∫ √

( 2 + 2 + 2) =

( 2 + 2 + 2)

+ ( , ) =

3 + ( , ).

2 + 2 + 2

Далее подставляем функцию ( , , ) =

3 + ( , ) во второе и третье

уравнения нашей системы:

(

3 + ( , )) = 2∙ ′ + ′

( , ) = 2∙

+ ′ ( , )

= ∙ + ′ ( , ) = ∙

′

( , ) = 0;

(

3 + ( , )) = 2∙ ′

+ ′( , ) = 2∙

+ ′( , ) = ∙ + ′( , ) = ∙

′

( , ) = 0;

′

( , ) = 0

{

( , ) = = ( , , ) =

3 + , = .

( , ) = 0

′

Ответ: =

Для центральных полей ( ) = ( )∙ градиент можно искать в виде = ( ).

Учитывая, что = ′( )∙ , неизвестную функцию ( ) можно найти из дифференциального уравнения: ′( )∙1 = ( ) ′( ) = ( )∙ .

Таким образом, потенциал центрального векторного поля ( ) = ( )∙ имеет вид:

= ( ) = ∫ ( ) ∙ .

Пример 4.18.

Найти потенциалы следующих центральных векторных полей ( = ):

а) ( ) = ∙ ;

б) ( ) =

∙ ;

в) ( ) =

∙ ;

г) ( ) =

∙ .

Решение.

( ) = ∙ ( ) = ( ) = ∫ ∙ = ∫ 2 =

3 + =

( ) =

∙ ( ) =

( ) = ∫

∙ = ∫ = + = ;

( ) =

∙ ( ) =

( ) = ∫

∙ = ∫

= ∙ + = ∙ ;

( ) =

∙ ( ) =

( ) = ∫

∙ = ∫

= −

+ = −

Ответ: а) =

б) = ; в) = ∙ ; г) = −

Рассмотрим некоторые приложения теории потенциальных полей в электротехнике.

Задачи на вычисление потенциалов электрического поля. Задача 1.

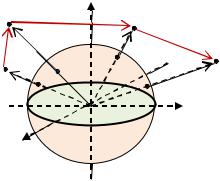
Дан бесконечно длинный проводящий цилиндр радиуса с линейной плотностью заряда , расположенный в среде с диэлектрической проницаемостью 0 (рис. 4.22).

Рис. 4.22. Иллюстрация к задаче 1

Напряженность электрического поля в точках , удаленных от оси цилиндра на расстояние ( > ), определяется равенством:


( ) =	20	∙		,

где – вектор, перпендикулярный оси цилиндра и соединяющий эту ось с точкой . Точки , , , удалены от оси цилиндра на расстояния соответственно

, , , (рис. 4.22). Требуется найти:

1)потенциалы точек и (приняв = 0 на поверхности цилиндра);

2)разность потенциалов между точками и ;

3)работу электрического поля по перемещению заряда по контуру [ ].

Решение.

Введем систему координат - так, как показано на рисунке 4.22: плоскостьпроведем через точку перпендикулярно оси цилиндра, а ось направим по оси цилиндра.

Тогда имеем: = + ( )

= 2∙ – плоское центральное векторное поле,

где =

; следовательно, потенциал равен

= ∙ + (см. Пример 4.18).

2 0

При = имеем: = 0, значит

∙ + = 0 = −∙ .

1) ( ) = ∙ −∙ = ∙

. Аналогично, имеем:

( ) = ∙

2) ∆ = ( ) − ( ) = ∙

−∙

= ∙

3) Так как

( ) - потенциальное поле, то работа равна разности потенциалов в

конечной и начальной точке:

(

)

(

)

= ∙ .

= ∫[ ]( ∙ ) =

−

Ответ:

1) ( ) =

∙

, ( ) =

∙

;

2) ∆ =

∙

; 3)

∙

Задача 2.

Дан проводящий шар радиуса , расположенный в среде с диэлектрической проницаемостью 0; заряд шара равен .

Напряженность электрического поля в точках , удаленных от центра шара на расстояние ( > ), определяется равенством:

( ) = 40 2∙ ,

где – радиус - вектор, соединяющий центр шара с точкой .

Точки , , , удалены от центра

шара на расстояния соответственно

, , , (рис. 4.23). Требуется найти:

1) потенциалы точек и

(приняв = 0 в бесконечно удаленной точке);

2) разность потенциалов между точками и ;

3) работу электрического поля

по перемещению заряда по контуру [ ].

Решение.

Введем систему координат

с началом координат в центре шара (рис. 4.23).

Рис. 4.23.

Иллюстрация

к задаче 2

( ) =

∙

- центральное векторное поле,

где =

;

следовательно, потенциал равен

= −

+ (см. Пример 4.18).

4 0

При = ∞ имеем: = 0,

значит = 0 = −

( ) = −

, ( ) = −

;

2) ∆ = ( ) − ( ) = (

−

);

3)Так как ( ) - потенциальное поле, то работа равна разности потенциалов

вконечной и начальной точках:

							(		)	(	)			1		1

												= (			− ).
	= ∫[ ]( ∙ ) =									−		= (			− ).
Ответ:
1) ( ) = −		∙	1	, ( ) = −		∙	1	;		2) ∆ =			(	1	−		1	);	3) =		(	1	−	1	).
1) ( ) = −		∙		, ( ) = −	40	∙		;		2) ∆ =		40	(		−			);	3) =	40	(		−		).
	40				40							40								40

4.4.2. Соленоидальные поля

Определение 4.17.

Векторное поле { = ( ), } - называется соленоидальным (трубчатым), если существует такое векторное поле { 0 = 0( ), }, ротор которого совпадает с вектором ( ) в любой точке области :

( ) = 0( ) .

Другими словами, соленоидальное поле – это поле роторов.

Если ( ) = ( , , )∙ + ( ,

, )∙ + ( , , )∙ , то соленоидальность этого

поля означает существование такой векторной функции (векторного потенциала)

0( , , ) = 0( , , )∙ + 0( , , )∙ + 0( , , )∙ , для которой выполняются

следующие равенства:

−

= ( , , )

−

= ( , , )

( , , ) .

{

−

= ( , , )

Например, векторное поле угловых скоростей тела, вращающегося вокруг

неподвижной оси, является соленоидальным полем (см. п. 4.3.3), так как

= 2 , т.е. = (2

- векторное поле линейных скоростей.

где 2 - векторный потенциал, а

Основные свойства соленоидального поля.

1. Соленоидальное поле - это поле без стоков и источников (т.е. дивергенция в каждой точке равна нулю): (( )) = 0 .

Это следует из свойства ротора: (( )) = ( 0( )) = 0 (см. п. 4.3.3).

Оказывается, справедливо и обратное утверждение: если дивергенция векторного поля в каждой точке равна нулю, то это поле – соленоидальное. Доказательство этого утверждения есть в работе [1].

2. В соленоидальном поле поток вектора через любую замкнутую поверхность

равен нулю: ( ∙ 0) = 0.

Это следует из формулы Остроградского (см. п. 4.2.3):

( ∙ 0) = Ω ( ) = Ω 0 = 0.

Далее рассмотрим отрезок векторной трубки с боковой поверхностью 0 между двумя ее произвольными сечениями 1 и 2 (рис. 4.24).

3. В соленоидальном поле поток вектора через любое поперечное сечение векторной трубки сохраняет постоянное значение:

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1312 13 > Следующая >>>

Соседние файлы в папке Экзамен

#
05.06.2021154.18 Кб8Вопросы к экзамену.pdf
#
05.06.202110.65 Mб17Все лекции.pdf
#
05.06.2021101.62 Кб6Дополнительные вопросы.pdf