Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

Все лекции

.pdf

Скачиваний:

Добавлен:

05.06.2021

Размер:

10.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1311 12 13 > Следующая >>>

Покажем это. Направим ось по оси вращения. Как известно из курса физики, линейная скорость точки равна векторному произведению вектора угловой скорости на радиус-вектор точки :

= × .

Найдем координатные функции вектора .

Так как вектор угловой скорости направлен по оси ,

то имеем {0, 0, }.

Тогда для любой точки ( , , ) можно вычислить координаты вектора с помощью определителя 3-го порядка:

Рис. 4.7. Векторное поле линейных скоростей

| = − |

= |0

| = −∙ + ∙ {− , , 0}.

Таким образом, поле линейных скоростей тела, вращающегося с постоянной

угловой скоростью вокруг неподвижной оси, есть плоское векторное поле:

( , )∙ + ( , )∙ ,

для которого ( , ) = −, ( , ) = .

Еще один пример плоского векторного поля дает

магнитное поле, создаваемое бесконечным проводником

электрического тока (рис. 4.8).

Это следует из формулы для вектора напряженности

магнитного поля, создаваемого электрическим током :

= ,

= 2∙( × ),

где

- радиус-вектор точки, - расстояние от точки

до проводника

Действительно, после введения декартовой системы

Рис. 4.8. Магнитное

координат так, чтобы вектор был направлен по оси ,

поле напряженности

получим:

∙ |0

| = −

∙|

| =

∙(− ∙ + ∙ ) {−

∙ ,

∙ , 0}.

Таким образом, магнитное поле , создаваемое бесконечным проводником

электрического тока , есть

плоское векторное поле: = ( , )∙ + ( , )∙ , для

которого ( , ) = −

∙ ,

( , ) =

∙ , где 2 = 2 + 2,

= | |.

4.2.2. Векторные линии и векторные поверхности

Наглядной геометрической характеристикой векторного поля является семейство

векторных линий этого поля.

Определение 4.8.

Векторной линией векторного поля { = ( ), } называется линия,

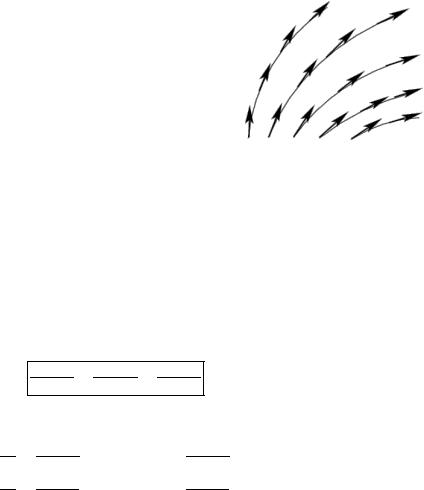
касательная к которой в каждой точке имеет направление вектора ( ). Примером векторных линий являются силовые линии в электромагнитном поле

(рис. 4.9).

В случае стационарного (т.е. не зависящего от времени) течения жидкости (или газа) векторные линии можно рассматривать как траектории движения частиц этой жидкости (или газа), т.е. линии тока.

Составим уравнения этих векторных линий.

= ( )

Пусть : { = ( ), [ ; ] – параметрические

= ( )

уравнения гладкой векторной линии векторного поля

Рис. 4.9. Силовые линии

( ) = ( , , )∙ + ( , , )∙ + ( , , )∙ .

электромагнитного поля

Как известно, касательным вектором к линии

в точке ( ( ), ( ), ( )) является вектор {′( ), ′( ), ′( )} (см. п. 3.1.3).

Из условия коллинеарности векторов:

- получаем пропорциональность

соответствующих координат этих векторов:

′( )

( , , )

Полученные уравнения составляют систему дифференциальных уравнений векторных линий:

( , , ) = ( , , ) = ( , , ) .

Эта система может быть записана и в виде нормальной системы дифференциальных уравнений:

= ( , , ) { ( , , )

= ( , , )( , , )

′( ) = ( , , )

{ ( , , ),′( ) = ( , , )( , , )

где = ( ) и = ( ) – искомые функции.

В случае плоского векторного поля: ( ) = ( , )∙ + ( , )∙ - получаем следующую систему дифференциальных уравнений векторных линий:

					{ ′( ) =	( , )
	=		=			( , )

						( , ).
( , )		( , )		0		( , ).
( , )		( , )		0	=

Замечание 4.3.

Пусть векторное поле { = ( ), } задается непрерывно-дифференцируемой

вектор - функцией ( ), которая нигде не обращается в нулевой вектор. Тогда можно доказать, опираясь на теоремы существования решений дифференциальных уравнений, что вся рассматриваемая область заполняется векторными линиями.

При этом через каждую точку области проходит одна и только одна такая линия. Векторные линии между собой не пересекаются.

Пример 4.7.

Найти векторные линии поля линейных скоростей тела, вращающегося с постоянной угловой скоростью вокруг оси .

Решение.

Линейная скорость определяется равенством: = −∙ + ∙ (см. п. 4.2.1). Составим систему дифференциальных уравнений векторных линий:

					′( ) = −
	=	=		{		.
−			0		=

Первое уравнение этой системы является дифференциальным уравнением с

разделяющимися переменными. Найдем его решение методом разделения переменных и

последующего интегрирования:

∙ = −∙ ∫ + ∫ =

−

= 2

= 1, 1

≥ 0.

Таким образом, векторные линии

задаются системой уравнений:

{

2 + 2 =

= , ≥ 0,

1, где ,

= 2

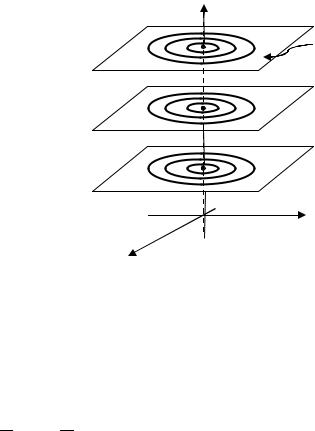
и представляют собой концентрические

окружности с центрами на оси , лежащие

в плоскостях, перпендикулярных этой оси

(рис. 4.10).

Ответ:

{

+ 2 =

, = ,

≥ 0.

= 2

Пример 4.8.

Рис. 4.10. Векторные линии

Найти векторные линии магнитного поля

в Примерах 4.7 и 4.8

бесконечного проводника тока: =

2∙( × ), = ,

где

- радиус-вектор точки, - расстояние от точки до проводника.

Решение.

Магнитное поле

бесконечного проводника тока задается формулой (см. п. 4.2.1):

= − 2∙ ∙ + 2∙ ∙ .

Составим и решим систему дифференциальных уравнений векторных линий:

′( ) = −

2 + 2 =

{

1, ,

= .

1 2

−

= 2

− 2∙

2∙

Векторные линии здесь также представляют собой концентрические окружности с центрами на оси , лежащие в плоскостях, перпендикулярных этой оси (рис. 4.10).

Ответ: { 2 + 2 = 1, 1, 2 = , 1 ≥ 0.= 2

Пример 4.9.

Найти векторную линию векторного поля ( ) = − + + , = ,

проходящую через точку (1, 0, 0).

Решение.

{

Дифференциальные уравнения векторных линий:

−

2 + 2 = { = √1

∙ (при ≥ 0);

√

1∙

−

√1∙

= √1

∙

= = + 2. Параметрические уравнения векторных линий имеют вид:

= √1 ∙

	∙ , −∞ < < +∞. Векторная линия проходит через точку (1, 0, 0),
{ = √
1
= + 2
	1 = √1 ∙
		∙ .
следовательно, имеем: {0 = √		∙ .
1
	0 = + 2
Решая эту алгебраическую систему
Решая эту алгебраическую систему
относительно 1, 2, получим: 1 = 1, 2 = 0.
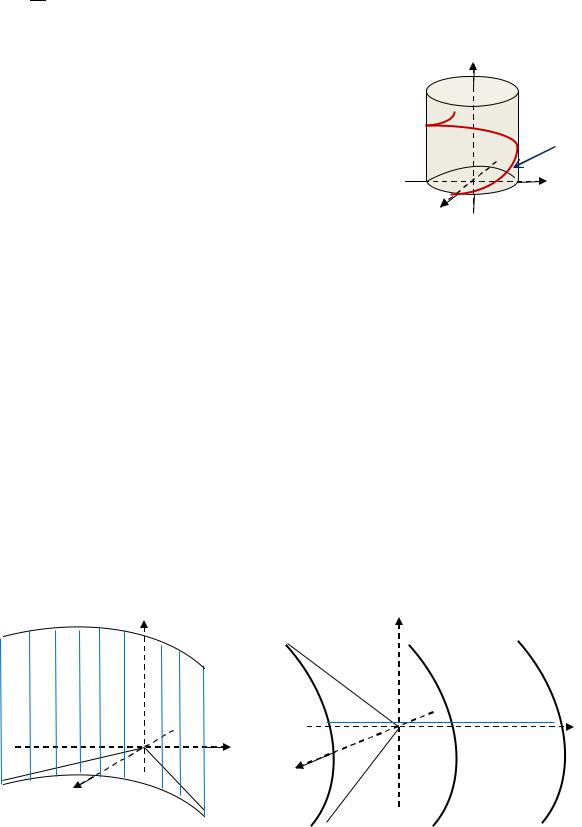
Ответ: Векторной линией является винтовая линия:			1
Ответ: Векторной линией является винтовая линия:
	=
: { = , −∞ < < +∞ (рис. 4.11).

	=	Рис. 4.11. Винтовая линия
		из Примера 4.9
	Пример 4.10.

Найти векторную линию векторного поля ( ) = + + , проходящую через точку (2, 1, 0).

Решение.


			′( ) =
			′( ) =
Дифференциальные уравнения векторных линий:	=	=	{ ′( ) =	.
Дифференциальные уравнения векторных линий:	=	=		.

Решая каждое из двух уравнений с разделяющимися переменными, получим:

{

2 − 2

= 3

2 − 2 =

1. Подставляя точку (2, 1,

0), получим: { 1

2 = 4

{

2 − 2

= 3

- линия пересечения двух гиперболических цилиндров

и ,

2 − 2

= 4

где :

2 − 2 = 3 - гиперболический цилиндр с образующей, параллельной оси и с

направляющей гиперболой, лежащей в плоскости (рис. 4.12);

: 2

− 2 = 4 - гиперболический цилиндр с образующей, параллельной оси

и с

направляющей гиперболой, лежащей в плоскости (рис. 4.13).

− 2 = 3

− 2 = 4

Рис. 4.12. Гиперболический

Рис. 4.13. Гиперболический

цилиндр

−

цилиндр

−

Ответ: Векторная линия : { 2 − 2 = 3 - линия пересечения двух гиперболических

2 − 2 = 4

цилиндров.

Векторные поверхности и векторные трубки.

Поверхности, составленные из векторных линий, называются векторными поверхностями.

Векторная поверхность характеризуется тем, что в каждой ее точке вектор( ) лежит в касательной плоскости к данной поверхности в этой точке (рис. 4.14) и,

следовательно, ортогонален вектору нормали
следовательно, ортогонален вектору нормали	в этой точке:		( ) ( ) .
Векторную поверхность можно
построить мысленно следующим образом.
Если взять в рассматриваемой области
Если взять в рассматриваемой области
какую-нибудь линию 0 («направляющую»),	0
отличную от векторных линий, и через	0
отличную от векторных линий, и через
каждую ее точку провести векторную линию,
то множество всех точек этих векторных линий			( )
и образует векторную поверхность.			( )
и образует векторную поверхность.
В случае, когда эта «направляющая»
является замкнутой линией, получается		Рис. 4.14. Векторная трубка
трубкообразная векторная поверхность,
которая называется векторной трубкой (рис. 4.14).

4.2.3. Поток векторного поля через замкнутую поверхность

Пусть имеется векторное поле { = ( ), } и ориентированная поверхность. По аналогии с п. 3.3.2 определим поток П векторного поля через поверхность по направлению вектора 0 как поверхностный интеграл 2 рода от вектор-функции ( ):

П( )∙

== ( ∙ 0)

Если - замкнутая поверхность, ограничивающая некоторое тело Ω, то поток записывается в виде:

П =
П =	( )∙ = ( ∙ 0)

В этом случае за направление вектора нормали принимается внешняя нормаль
(поток изнутри поверхности ).			0
Физический смысл потока через замкнутую поверхность.			0
Физический смысл потока через замкнутую поверхность.
Пусть вектор ( ) задает поле скоростей		0
движения частиц некоторого вещества, например
жидкости или газа, через замкнутую поверхность .
Обозначим через + ту часть поверхности ,
Обозначим через + ту часть поверхности ,
в точках которой вектор ( ) образует с вектором 0
острый или прямой угол (векторные линии выходят из			0
тела Ω или касаются его); через − обозначим ту часть
поверхности , в точках которой вектор ( ) образует		Рис. 4.15. Поток через
с вектором 0 тупой угол (векторные линии входят в тело Ω).		замкнутую поверхность

Тогда поток через замкнутую поверхность равен разности количества вещества, вытекающего из тела Ω и втекающего в него (рис. 4.15): П = П+ − П−.

При этом если П > 0 (П+ > П−), то через поверхность вытекает больше вещества, чем втекает. Это означает, что внутри тела Ω имеются дополнительные

источники.

Если же П < 0 (П+ < П−), то внутри тела Ω имеются стоки, поглощающие избыток вещества.

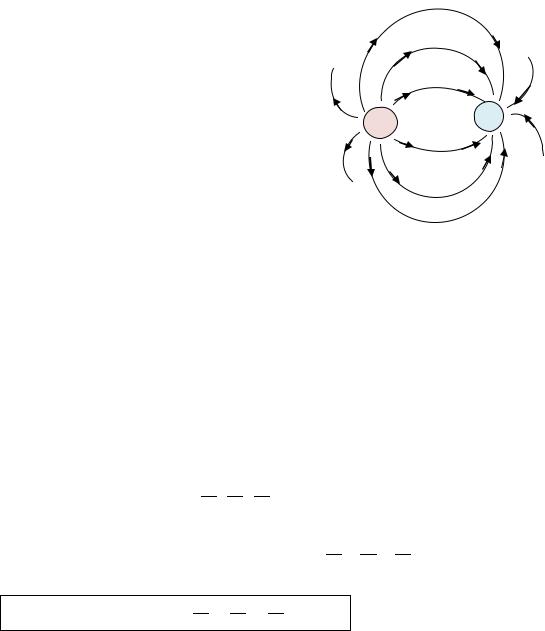
Другими словами, источники – это точки, откуда векторные линии начинаются, а стоки – точки, где векторные линии заканчиваются.

К примеру, в электростатическом поле точечного заряда источником является положительный заряд, а стоком – отрицательный заряд (рис. 4.16).

Если П = 0, то из тела Ω вытекает столько же вещества, сколько в него и втекает; значит, внутри тела Ω либо нет ни источников, ни стоков, либо они таковы, что их действие взаимно компенсируется.

+ −

Рис. 4.16. Источники и стоки в

электростатическом поле

Поток П = ( ∙ 0) через замкнутую поверхность иначе называют еще

производительностью (источников и стоков) векторного поля ( ) внутри пространственной области (тела) Ω.

Рассмотрим поток векторного поля ( ) = ( , , )∙ + ( , , )∙ + ( , , )∙ ,

( , , ) через произвольную замкнутую поверхность , ограничивающую некоторое тело Ω. Справедливо следующее утверждение.

Теорема 4.2 (Остроградского).

Пусть функции ( , , ), ( , , ), ( , , ) непрерывны в области и имеют там непрерывные частные производные , , . Пусть – произвольная кусочно-гладкая замкнутая поверхность в области . Тогда поток П векторного поля ( ) через поверхность равен тройному интегралу от функции + + по телу,

ограниченному этой поверхностью:

П = ( ∙ 0) = Ω ( + + ) - формула Остроградского.

Доказательство теоремы Остроградского можно найти в работах [1], [2].

Следствие 4.3.

Поток радиус-вектора точки ( ) через любую замкнутую кусочно-гладкую поверхность равен утроенному объему тела Ω, ограниченного этой поверхностью:

	П =	( ∙ 0) = 3 (Ω).

Действительно, имеем:
				( ∙ 0) =	3 = 3 (Ω).

( ) = ∙ + ∙ + ∙	+ +		= 3
				Ω

Замечание 4.4.

В п. 3.3.3 непосредственно вычислены потоки радиус-вектора точки ( ) через замкнутые поверхности тетраэдра, сферы и цилиндра (см. Примеры 3.7, 3.8, 3.9). Если же использовать формулу Остроградского и Следствие 4.3, то можно сразу получить те же результаты:

= 3

= 3∙

∙

; П

= 3 = 3∙

∙ 3

= 43;

сферы

тетр.

3 2

шара

Пцил. = 3цил. = 3∙ 2 = 32 .

4.3. Основные свойства векторного поля

Основные свойства векторного поля связаны с такими понятиями, как дивергенция, циркуляция и ротор. Перейдем к рассмотрению этих понятий.

4.3.1. Дивергенция векторного поля

Пусть - замкнутая поверхность, ограничивающая тело Ω. Тогда отношение потока векторного поля ( ) через замкнутую поверхность к объему тела Ω, т.е.

величина: (1Ω)∙ ( ∙ 0) - будет средней объемной плотностью потока через

замкнутую поверхность (или средней плотностью источников и стоков, или средней производительностью источников и стоков).

Пусть – некоторая фиксированная точка, лежащая внутри тела, ограниченного поверхностью . Будем «стягивать» поверхность к точке так, чтобы эта точка находилась внутри тела, а диаметр стремился к нулю: { } → .

Определение 4.9.

Если существует конечный предел				1		∙	( ∙ ) , то он называется

		{ } → (Ω)					0

дивергенцией (расходимостью) векторного поля в точке и обозначается								( ):
( ) =		1	∙		( ∙ ) .

	{ } → (Ω)						0

Дивергенция ( ) характеризует векторное поле в самой точке , а именно:

-если ( ) > 0, то в точке имеется источник;

-если ( ) < 0, то в точке имеется сток;

-если ( ) = 0, то в точке нет ни источника, ни стока.

Следовательно, дивергенция векторного поля ( ) в области - это скалярная функция, характеризующая распределение и производительность источников и стоков этого поля в области .

Введем обозначение: ( ) = ( , , ) + ( , , ) + ( , , ).

Тогда из формулы Остроградского и теоремы о среднем для тройного интеграла (см. п. 1.5.3) имеем:

( ∙ 0) =

( ) = (ср)∙(Ω)

( ) =

∙(

)∙(Ω) =

(

) = ( ) =

{ } → (Ω)

ср

{ } →

ср

В результате получаем формулу для вычисления дивергенции:

( ) = + + .

Теорему 4.2 (Остроградского) теперь можно дать в следующей формулировке.

Поток векторного поля через любую замкнутую поверхность равен тройному интегралу от дивергенции векторного поля по телу, ограниченному этой поверхностью:

( ∙ 0) = Ω ( ) - формула Остроградского.

Правила вычисления дивергенции.


Используя обозначение оператора Гамильтона: =	∙ +	∙ +		∙ , можно
представить дивергенцию как скалярное произведение векторов			и :

∙ = (

∙ +

∙ )∙( ∙ + ∙ + ∙ ) =

= .

Таким образом, дивергенция есть оператор, преобразующий векторную величину в скалярную величину и определяемый равенством:

= ∙ .

Отметим следующие правила вычисления дивергенции.

(1)= 0 , где = .

(2)( ∙ ) = ∙ , где = .

(3)( 1 + 2) = 1 + 2.

(4)( ∙ ) = ∙ + ∙ , где - скалярная функция, - градиент .

Эти правила легко выводятся из формулы: ( ) = + + .

Например, правило (4):

∙ = ∙( ∙ + ∙ + ∙ ) = ∙ ∙ + ∙ ∙ + ∙ ∙

( ∙ ) = ( ∙ ) + ( ∙ ) + ( ∙ ) =

=∙ + ∙ + ∙ + ∙ + ∙ + ∙ = ∙( + + ) +


+ ∙		+ ∙		+ ∙		= ∙ + ∙ .

Замечание 4.5.

Правила (2) и (3) означают, что дивергенция - это линейный оператор.

Дивергенция центрального векторного поля.

Определение 4.10.

Векторное поле вида: ( ) = ( )∙ , где { , , } - радиус-вектор точки,

= | | = √2 + 2 + 2 - называется центральным векторным полем.

Пример 4.11.

Найти ( ( ) ∙ ), где { , , } - радиус-вектор точки, = | | = √2 + 2 + 2.

Решение.

′

= ( ∙ + ∙ + ∙ ) = 3;

( ) =

( )∙

(см. Пример 4.6).

′

По правилу (4) имеем: ( ( ) ∙ ) = ( )∙ + ∙ ( ) = 3 ( ) + ∙

( )∙ =

= 3 ( ) + ′( )∙

= 3 ( ) + ∙ ′( ).

Ответ: ( ( ) ∙ ) = 3 ( ) + ∙ ′( ).

Пример 4.12.

Найти (

∙ ), где = .

Решение.

Применим результат Примера 4.11,

где ( ) =

′( ) = (

)′ = −

В результате получим: (

∙ ) = 3

+ ∙(−

) = 3

−

= 0.

Ответ: (

∙ ) = 0.

4.3.2. Циркуляция векторного поля

Рассмотрим криволинейный интеграл 2 рода ∫

( )∙ вдоль кусочно-гладкой

Рис. 4.19.

Поверхность, натянутая на контур

кривой : ∫	(	)		{			(	, ,	)	+	(	, ,	)	+	(	, ,	)	}	.
кривой : ∫		∙ = ∫						, ,		+		, ,		+		, ,			.

Далее этот интеграл будем называть линейным

интегралом от векторного поля ( ) вдоль кривой .

Определение 4.11.
Линейный интеграл вдоль замкнутой кривой
(замкнутого контура) называется циркуляцией Ц
(замкнутого контура) называется циркуляцией Ц
векторного поля ( ) вдоль этой кривой (рис. 4.17):														0
					)
			(		)
Ц = ( ∙ ) =						∙ , или:
Ц = { ( , , ) + ( , , ) + ( , , )}.														Рис. 4.17.			Иллюстрация к
Физический смысл циркуляции.														Рис. 4.17.			Иллюстрация к
Физический смысл циркуляции.

В силовом поле циркуляция равна работе силы	понятию циркуляции

по перемещению материальной точки вдоль замкнутой кривой.
Пример 4.13.

Найти циркуляцию Ц векторного поля линейных скоростей тела, вращающегося с постоянной угловой скоростью вокруг оси вдоль произвольной замкнутой кривой, лежащей в плоскости, перпендикулярной оси вращения (рис. 4.18).

Решение.

В п. 4.2.1 показано, что векторное поле


линейных скоростей является плоским
векторным полем, которое имеет вид:

= −∙ + ∙ .
Пусть - произвольная замкнутая кривая	O
Пусть - произвольная замкнутая кривая

в плоскости = (рис. 4.18).

Тогда имеем: Ц = (− ∙ + ∙ ) =	Рис. 4.18.	Иллюстрация к
= ∙ (− ∙ + ∙ ).	Примеру 4.13

Учитывая, что ( − ) = 2∙( ) – площадь плоской фигуры, ограниченной замкнутой кривой (см. п. 2.5.2), получим: Ц = 2∙( ).

	Ответ: Ц = 2∙( ).
	Если замкнутая кривая в пространстве ограничивает
	Если замкнутая кривая в пространстве ограничивает
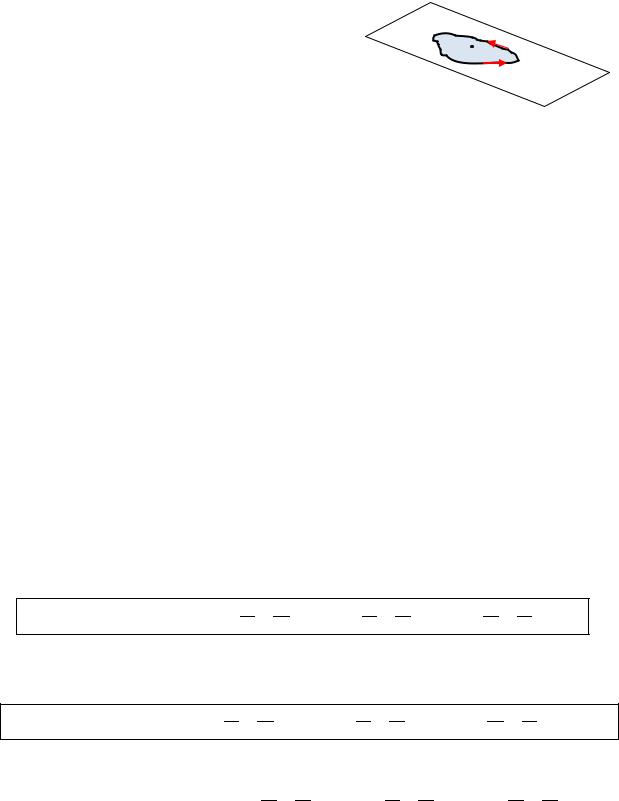
	некоторую (незамкнутую) поверхность , то говорят, что
	некоторую (незамкнутую) поверхность , то говорят, что
	поверхность «натянута» на контур (рис. 4.19).
	В частности, если контур - плоский, то ограниченная
	В частности, если контур - плоский, то ограниченная
	этим контуром область также считается «натянутой» на контур.
	Предполагается, что ориентации контура и поверхности

(т.е. вектора нормали ) - согласованы. Это означает, что обход контура должен быть таким, чтобы прилегающая часть поверхности оставалась слева от направления движения

по контуру (рис. 4.19). При этом движущийся по контуру объект ориентирован так, что вектор нормали пронизывает его «от ног к голове».

Ниже будет показано, что имеется непосредственная связь между циркуляцией по контуру и поверхностным интегралом по поверхности, натянутой на этот контур.

Плотность циркуляции.

Далее мы рассматриваем циркуляцию вдоль плоских замкнутых контуров.

Пусть – замкнутый контур в плоскости (с вектором нормали ), ограничивающий плоскую область (рис. 4.20). Тогда отношение циркуляции по контуру к площади области , т.е. величина:

1
(D)∙		( ∙ ) - будет средней (плоскостной)

Рис. 4.20. Иллюстрация к

понятию плотности циркуляции

плотностью циркуляции по контуру в направлении вектора .

Выберем некоторую точку и будем «стягивать» контур к точке (т.е. точка находится внутри контура, а диаметр области стремится к нулю): { } → .

Определение 4.12.

Если существует конечный предел					1
Если существует конечный предел						∙ ( ∙ ), то он называется
			{ } → (D)
								и
плотностью (плоскостной) циркуляции в точке в направлении вектора								и
обозначается ( ):

( ) =		1
( ) =				∙ ( ∙ ).
	{ } → (D)
Рассмотрим векторное поле:
							( , , ) .
( ) = ( , , )∙ + ( , , )∙ + ( , , )∙ ,							( , , ) .
Пусть - замкнутый контур и		- произвольная поверхность, натянутая
на этот контур. Справедливо следующее утверждение.
Теорема 4.3 (Стокса).
Пусть функции ( , , ), ( , , ),			( , , ) непрерывны вместе со своими

частными производными 1-го порядка в области .

Тогда для любого замкнутого контура и для любой поверхности , натянутой на контур , справедлива следующая формула Стокса, связывающая циркуляцию векторного поля ( ) по контуру с поверхностным интегралом 2-го рода по поверхности :

( + + ) = {( − ) + ( − ) + ( − ) } .

Доказательство теоремы Стокса приведено в работах [1], [2].

Учитывая связь между поверхностными интегралами 1 и 2 рода, формулу Стокса можно записать в следующем виде:

( + + ) = {( − ) ∙ + ( − ) ∙ + ( − ) ∙ γ} ,

где , , γ - направляющие углы единичного вектора нормали 0( ) в точке , а интеграл в правой части равенства есть поверхностный интеграл 1 рода.

Введем обозначение: ( ) = ( − ) + ( − ) + ( − ) γ.

Тогда формула Стокса запишется в виде: Ц =		( ) .
	( ∙ ) =

Символически функцию ( ) можно представить в виде определителя 3-го порядка, или в виде скалярного произведения векторов:

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1311 12 13 > Следующая >>>

Соседние файлы в папке Экзамен

#
05.06.2021154.18 Кб8Вопросы к экзамену.pdf
#
05.06.202110.65 Mб17Все лекции.pdf
#
05.06.2021101.62 Кб6Дополнительные вопросы.pdf