Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

Все лекции

.pdf

Скачиваний:

Добавлен:

05.06.2021

Размер:

10.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 138 9 10 11 12 13 > Следующая >>>

′	(	′	(	′	′	(	′	′
	(	)∙	(	) +	( )∙	(	) +	( )∙	( ) = 0 ∙ = 0.
	0		0		0	0		0	0

Последнее равенство означает, что векторы и - ортогональны: . Заметим, что вектор зависит от кривой , а вектор - один и тот же для всех

кривых, лежащих на поверхности и проходящих через точку 0.

Таким образом, получаем, что все кривые, лежащие на поверхности и проходящие через точку 0, имеют касательные, перпендикулярные одному и тому же вектору - градиенту функции ( , , ) в точке 0.

Это означает, что все касательные лежат в одной плоскости, а именно: в плоскости, проходящей через точку 0 и перпендикулярной вектору . Эту плоскость называют касательной плоскостью.

Определение 3.6.

Касательной плоскостью к поверхности в точке 0 называется плоскость, проходящая через все касательные прямые к кривым, лежащим на этой поверхности и проходящим через точку 0.

		Уравнение касательной плоскости имеет вид:
′ ( , , ) ∙ ( −						) + ′		( , , ) ∙ ( − ) + ′ ( , ,																) ∙ ( − ) = 0, или:
	0 0 0				0		0 0 0									0			0 0 0							0
			′	(	) ∙ ( − ) + ′ (						) ∙ ( −					) + ′			(		) ∙ ( −					) = 0		.
				0		0				0				0						0					0
Определение 3.7.
		Прямая, проходящая через точку 0											и перпендикулярная касательной плоскости,
называется нормалью к поверхности в точке 0.
												− 0				=		− 0				=		− 0
		Уравнения нормали имеют вид:																									, или:
		Уравнения нормали имеют вид:									′	(		, , )			′	(		, , )			′	(		, , )	, или:
												0		0 0				0		0 0					0	0 0

							− 0		=	− 0			=		− 0		.
							′ ( )		=	′	(	)	=		′ ( )		.
							′ ( )			′	(	)			′ ( )
								0			0					0
Замечание 3.3.
		Уравнения нормали и касательной плоскости теряют смысл, если
′	(	) = ′ ( )			= ′ ( ) = 0.				В этом случае точка ( , ,																) называется особой
	0			0		0														0	0	0 0

точкой поверхности . В особых точках поверхности касательная плоскость и нормаль к поверхности не существуют.

	′	(	),	′	(	),	′	( )}	отлична
Если же хотя бы одна из координат вектора {
		0			0			0
от нуля, то точка 0(0, 0, 0) называется обыкновенной точкой поверхности .									В таких

точках поверхности касательная плоскость и нормаль существуют, и они единственны. Рассмотрим частный случай, когда поверхность задается уравнением:

= ( , ).

В этом случае имеем:

( , , ) = − ( , ),

′

= −

′

, 1}.

= −

= 1 {−

, −

Уравнение касательной плоскости:

−

′( , )

∙ ( − ) + ′( , )

∙ ( − );

0 0

уравнения нормали:

− 0

′( ,

)

′

(

, )

−1

0 0

Пример 3.2.

Составить уравнения касательной плоскости и нормали к поверхности = 2 + 2

в точке 0(1; −2; 5).

Решение.

Здесь имеем: ′ = 2,

′

= 2,

′( , )

= 2,

′( , )

= −4;

на касательную плоскость

1≤ ≤

уравнение касательной плоскости: − 5 = 2∙( − 1) − 4∙( + 2) 2 − 4 − − 5 = 0;

уравнения нормали:

−

+ 2

− 5

−4

−1

Ответ: 2 − 4 − − 5 = 0;

−

+ 2

− 5

−4

−1

3.1.5. Понятие площади кривой поверхности и ее вычисление

Рассмотрим в пространстве 3 поверхность

, ограниченную контуром .

Разобьем поверхность
на частичные поверхности:
на частичные поверхности:
=	… .
1		2
В каждой части			выбираем

промежуточную точку							и проводим

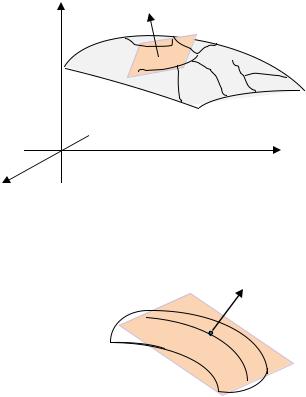
касательную плоскость				к поверхности

в точке (рис. 3.9).
											O
Далее проектируем частичную											O
Далее проектируем частичную
поверхность		с вектором нормали
поверхность		с вектором нормали

на касательную плоскость					(рис. 3.10),

= 1, … , .											Рис. 3.9.
Предполагаем, что диаметр
частичной поверхности				настолько мал, что

это проектирование будет взаимно-однозначным.
̃		- проекция				на касательную
Пусть		- проекция				на касательную

плоскость , а		̃
плоскость , а	( ) - ее площадь, = 1, … , .

Составим сумму: ̃					=	∑				̃	и введем
Составим сумму: ̃					=	∑		=1	( )		и введем
								=1

обозначение:

λ = { } - ранг разбиения поверхности .

Определение 3.8.

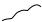
Разбиение поверхности и выбор промежуточных точек

Рис. 3.10. Проектирование

Если существует ̃ , не зависящий

λ → 0

ни от способа разбиения, ни от выбора промежуточных точек, то этот предел называется площадью поверхности :

( ) = ∑ (̃ ),

λ =1 → 0

а сама поверхность называется квадрируемой.

Таким образом, площадь кривой поверхности определяется как предел сумм площадей плоских фигур, полученных проектированием кривых поверхностей на касательные плоскости.

Вычисление площади кривой поверхности.

Пусть поверхность задана явным уравнением:

= ( , ),

где ( , ) - дифференцируемая функция 2-х переменных ( , ) 2.

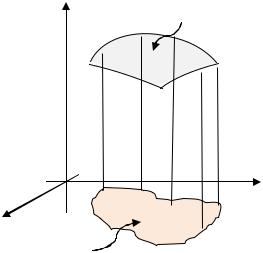
Поверхность , ограниченная некоторым контуром, проектируется на плоскостьв область (рис. 3.11). Выведем формулу для вычисления площади поверхности .

Разобьем область на частичные области: = 1 2 … и рассмотрим цилиндрические поверхности с образующими, параллельными оси и с основаниями

, = 1, … , .

Эти цилиндрические поверхности разбивают поверхность на

частичные поверхности:

… .

Выберем в каждой части

= ( , )

промежуточную точку

и проведем

касательную плоскость

к поверхности

в точке .

Далее продолжим эти цилиндрические

поверхности до пересечения с построенными

касательными плоскостями.

Тогда на этих плоскостях вырежутся

плоские области ′

с площадями (′ ),

= 1, … , .

Как было показано выше (см. 3.1.2),

площади (′ ) и (

) связаны формулами:

(

) = (′ )∙ γ

Рис. 3.11. Проекция поверхности

где γ - острый угол между касательной

на плоскость

плоскостью

и плоскостью , который

совпадает с углом между вектором нормали (градиентом) и осью .

По определению площади поверхности имеем:

( ) = ∑

( ),

λ → 0

на касательную плоскость .

где ( ) - площадь проекции

Примем без доказательства следующее утверждение.

Лемма 3.1.

Для поверхности , заданной явным уравнением:

= ( , ), следующие пределы

совпадают:

∑

(

′

( ) =

λ → 0

Согласно этой лемме, имеем:

( ) = ∑

∑

(

′

) =

∑

( )

∑

( ) =

∙ ∆ .

λ → 0

→ 0

λ → 0

Последнее выражение совпадает с пределом интегральных сумм для двойного

интеграла от функции

Таким образом, получаем формулу:

γ( , )

( )

γ( , )

где γ( , )- острый угол между вектором нормали и осью в точке ( , , ).

Для практических вычислений полученная формула не очень удобна, поэтому ее

надо преобразовать. Для этого вычислим γ( , ).

′

Так как γ = γ( , ) — это острый угол между вектором нормали {−

, − , 1}

оси , то справедливы следующие равенства:

ортом {0, 0, 1}

| ∙ |

√

′

γ( , ) =

√1 + (′)2 + (′)2

γ( , )

= | | =

1 + ( )

+ ( )

| |∙| |

| |

( ) =

√

′

| | =

1 + ( )

+ ( )

Таким образом, доказано следующее утверждение.

Теорема 3.3.

Пусть - гладкая поверхность, заданная явным уравнением: = ( , ), а область - ее проекция на координатную плоскость .

Тогда площадь поверхности вычисляется по формуле:

( ) = √1 + (′)2 + (′)2 .

Замечание 3.4.

Аналогичные формулы получаются в случае задания поверхности уравнениями

= ( , ) и = ( , ):

( ) = √1 + (′)2 + (′)2 и ( ) = √1 + (′)2 + (′)2 .

Общую формулу для площади поверхности можно записать в виде:

( ) =		, или	( ) =		, или	( ) =		,
( ) =	\| \|	, или	( ) =	\| \|	, или	( ) =	\| \|	,

где , , - проекции поверхности на координатные плоскости, соответственно, и , а - вектор нормали к поверхности в произвольной точке:

= ( , ) {−′ ; −′ ; 1}; = ( , ) {−′; 1; −′}; = ( , ) {1; −′ ; −′ }.

Пример 3.3.

Найти площадь поверхности сферы радиуса .

Решение.

Сфера радиуса задается уравнением:

2 + 2 + 2 = 2

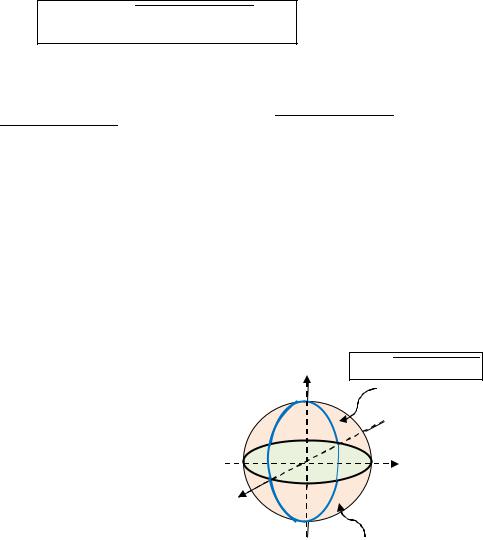
Вычислим сначала площадь поверхности верхней полусферы (рис. 3.12) с уравнением:

= √2 − 2− 2

= √2 − 2 − 2 .

Здесь имеем: ′ = −

′ = −

√ 2− 2

− 2

√ 2− 2− 2

1 + (′)2 + (′)2

= 1 +

2− 2− 2

= − √2 − 2− 2

√1 + (′)2 + (′)2 =

;

√ 2− 2− 2

Рис. 3.12. Иллюстрация

. Область — это круг

к Примеру 3.3

√

2− 2− 2

с центром в начале координат и радиуса .

Для вычисления двойного интеграла перейдем к полярным координатам:

= ∙

0 ≤ ≤

[ = ∙

∙ , где ′:

]

= ′

{0 ≤ < 2.

√

2− 2− 2

2− 2

|0 =

= ∫0

∫0

∙ = −

∫0

− 2) = − ∫0

(2 − 2) 2

√

2− 2

= ∫2

= 2∙2 = 22

= 42.

сферы

Ответ:

= 42.

сферы

3.2. Поверхностный интеграл 1 рода

Введенное выше понятие площади кривой поверхности позволяет нам перейти к рассмотрению нового типа интегралов – поверхностного интеграла 1 рода.

	3.2.1. Понятие поверхностного интеграла 1 рода
	Рассмотрим в пространстве
квадрируемую поверхность (рис. 3.13).
	Пусть на поверхности					задана
	Пусть на поверхности					задана
функция ( ),			.
	Выполним следующие действия.
1.	Разбиение поверхности на частичные
	поверхности:
		=				… .			O
				1	2
2.	Выбор промежуточных точек:
2.	Выбор промежуточных точек:
	,			= 1, 2, … , .

3.	Вычисление суммы:							Рис. 3.13. Поверхность в пространстве
	= ∑			( ) ∙ ∆ ,				Рис. 3.13. Поверхность в пространстве
	= ∑			( ) ∙ ∆ ,
		=1
	где ∆ = ( )			- площадь частичной поверхности , = 1, 2, … , .

	Сумма		называется интегральной суммой						Римана функции ( ) по

поверхности .		Пусть λ =					- наибольший из диаметров частичных поверхностей

1≤ ≤

- ранг разбиения.

Определение 3.9.

Число называется пределом интегральных сумм при λ → 0, если для > 0> 0 такое, что для любого разбиения поверхности с рангом разбиения λ < и при любом выборе промежуточных точек { }=1 выполняется неравенство:

	\|	− \| < .

Запись: = - означает, что при			λ → 0 этот предел существует, он не
λ → 0

зависит ни от способа разбиения, ни от выбора промежуточных точек, и равен числу .

Определение 3.10.

Конечный предел интегральных сумм при λ → 0 называется поверхностным интегралом 1 рода от функции ( ) по поверхности .

Обозначения: ( ) или

( , , ) .

Согласно определению имеем:

( ) =

∑

( ) ∙ ∆

или

λ → 0

( , , ) =

∑

( , , ) ∙ ∆

λ → 0

Функция ( ), для которой существует поверхностный интеграл 1 рода,

называется интегрируемой по поверхности .

Пример 3.4.

0 = ∑=1

0∙∆ = 0 = 0

0 = 0;

1 =

λ → 0

∑

1∙∆

= ( ) = ( ) - площадь поверхности .

λ → 0

Физический смысл поверхностного интеграла 1 рода.

Если ( ) - поверхностная плотность массы, распределенной на поверхности ,

то = ( ) - масса этой неоднородной поверхности.

Если ( ) - поверхностная плотность заряда, распределенного на поверхности ,

то = ( ) - электрический заряд поверхности . Условия интегрируемости.

Теорема 3.4 (необходимое условие интегрируемости).

Если функция ( ) интегрируема по поверхности , то она ограничена на этой поверхности.

(Обратное утверждение неверно: есть ограниченные, но не интегрируемые функции). Теорема 3.5 (достаточное условие интегрируемости).

Пусть - гладкая поверхность, а функция ( ) непрерывна на поверхности . Тогда функция ( ) интегрируема по поверхности .

3.2.2. Свойства поверхностного интеграла 1 рода 1. Нормированность.

Поверхностный интеграл 1 рода от единицы по поверхности равен площади этой поверхности:

1 = ( ).

2. Линейность.

Пусть функции ( ) и ( ) интегрируемы по поверхности . Тогда справедливы следующие утверждения.

а) постоянный множитель можно выносить за знак поверхностного интеграла 1 рода:

∙( ) = ∙ ( ) , = ;

б) поверхностный интеграл 1 рода от суммы функций равен сумме поверхностных интегралов 1 рода от этих функций:

( ( ) + ( )) = ( ) + ( ) .

Свойство линейности можно записать в следующем виде:

	(1	∙ ( ) + 2	∙ ( )) = 1∙	( ) + 2∙	( )	1, 2 = .

3. Аддитивность.

Пусть функция ( ) интегрируема по поверхности . Тогда справедливо следующее утверждение.

Если поверхность разбита на две части, то поверхностный интеграл 1 рода по всей поверхности равен сумме поверхностных интегралов 1 рода по каждой из этих частей:

	( ) =	( ) +	( ) ,	где = 1 2	и 1 ∩ 2 = .
	1	2

4. Интегрирование неравенств.

Пусть функции ( ), ( ) интегрируемы по поверхности и удовлетворяют неравенству: ( ) ≥ ( ) . Тогда справедливо неравенство:

( ) ≥ ( ) .

Следствие 3.1.

а) Если ( ) ≥ 0 , то ( ) ≥ 0.

б) Пусть ( ) ≥ 0 , тогда для любых поверхностей 1, 2 справедливо утверждение:

	1 2		( ) ≤	( ) .
		1	2
в) \|	( ) \| ≤	\|( )\|.

5. Оценки поверхностного интеграла 1 рода.

Если значения подынтегральной функции ( ) на поверхности ограничены величинами и , то значение интеграла ограничено величинами ∙( ) и ∙( ), где ( ) - площадь поверхности:

≤ ( ) ≤ ∙( ) ≤ ( ) ≤ ∙( ).

6. Теоремы о среднем значении. Теорема 3.6.

Пусть функция ( ) интегрируема по поверхности и пусть

= { ( ), };					= { ( ), }.
Тогда [ ; ]:				( ) = ∙( ), где ( ) - площадь поверхности.
Число =		1	∙	( ) - называется интегральным средним значением
	()

функции ( ) по поверхности .
Теорема 3.7.
Пусть функция ( ) непрерывна на поверхности . Тогда 0 :
( ) = (0)∙( ),						где ( ) - площадь поверхности.

Доказательство всех этих утверждений аналогично доказательству в случае кратных интегралов.

3.2.3. Вычисление поверхностного интеграла 1 рода

Вычисление поверхностного интеграла 1 рода ( ) сводится к вычислению двойного интеграла. Покажем это.

Теорема 3.8.

Пусть - гладкая поверхность, заданная явным уравнением: = ( , ), область - ее проекция на плоскость и ( , , ) - непрерывная функция, заданная на поверхности . Тогда поверхностный интеграл 1 рода вычисляется по формуле:

( , , ) = ( , , ( , )) ∙ √1 + (′)2 + (′)2 .

Доказательство.

По определению поверхностного интеграла 1 рода имеем:

( ) = ∑

( ) ∙ ∆ , или

λ → 0

( , , ) =

∑

( , , ) ∙ ∆ ,

λ → 0

где (

) - промежуточные точки на частичных поверхностях , полученных

при разбиении поверхности , а ∆

= ( ) - площади этих частичных поверхностей,

= 1, 2, … , .

Разбиение поверхности порождает разбиение области : = … .

По формуле для площади кривой поверхности (см. 3.1.5)

имеем:

∆

= ( ) =

| | ,

√

′

)

′

)

, а по теореме о среднем для двойного интеграла (см. п. 1.2.3)

где | | =

1 + (

+ (

можно записать:

̃′

)∙ ( ),

| | = | |(

′

- некоторая точка частичной области , а ( ) - площадь этой частичной

где

области.

Следовательно, имеем:

∑

( , ,

)∙∆

∑

( ,

, ( ,

̃′

)∙ ( ) =

))∙| |(

λ → 0

∑

( , , ( ,

))∙√1 +

( ′)2( ′ , ′ ) + ( ′)2( ′ , ′ )∙ ( ).

λ → 0

С другой стороны, по определению двойного интеграла имеем:

( , , ( , ))∙√1 + ( ′)2

+ ( ′)2

∑

( , , ( , )) ∙ √1 + (

′)2

( ,

) + ( ′)2

( ,

)∙ ( ).

λ → 0

Как видим, разница заключается лишь в значениях подкоренных выражений. В

одном случае это значение вычисляется в точках ′

( ,

), которые являются

проекциями произвольно взятых точек

( , ,

) на координатную плоскость , а

вдругом - в специальных (из теоремы о среднем) точках ̃′ ( ′ , ′ ), которые уже не

являются произвольными.

Однако можно показать (доказательство опускаем), что разность между этими интегральными суммами ввиду непрерывности подынтегральных функций стремится к нулю при λ → 0, а значит, одну сумму в пределе можно заменить другой суммой.

В результате получаем:

( ) =

∑

(

, (

, )) ∙ √1 +

( ′)2

( ′

, ′ ) + ( ′)2

( ′

, ′ )∙ ( ) =

λ → 0

∑

( , , ( ,

)) ∙

√1 + ( ′)2

( ,

) + ( ′)2( ,

)∙ ( ) =

λ → 0

= ( , , ( , )) ∙ √1 + ( ′)2 + ( ′)2 .

Теорема доказана.

Применение этой формулы обычно сопровождается следующей записью:

= ( , ), ( , )( , , ) = [ = √1 + ( ′)2 + ( ′)2 ] =

= ( , , ( , ))∙√1 + ( ′)2 + ( ′)2 .

Замечание 3.5.

Если поверхность задается уравнением: = ( , ), то поверхностный интеграл 1 рода вычисляется по формуле:

( , , ) = ( , ( , ), ) ∙ √1 + (′)2 + (′)2 ,

где область - это проекция поверхности на координатную плоскость .

Если поверхность задается уравнением: = ( , ), то поверхностный интеграл 1 рода вычисляется по следующей формуле:

( , , ) = ( ( , ), , ) ∙ √1 + (′)2 + (′)2 ,

где область - это проекция поверхности на координатную плоскость . В общем случае можно записать:

( , , ) = ( , , ( , )) ∙ | | , или:

( , , ) = ( , ( , ), ) ∙ | | , или:

( , , ) = ( ( , ), , ) ∙ | | ,

= ( , ) {−′ ; −′ ; 1}; = ( , ) {−′; 1; −′}; = ( , ) {1; −′ ; −′ }.

3.2.4. Приложения поверхностного интеграла 1 рода

Площадь поверхности : ( ) = 1.

Масса неоднородной поверхности : = ( , , ) , где ( , , ) – поверхностная плотность массы, распределенной на поверхности ;

Электрический заряд поверхности : = ( , , ) , где ( , , ) – поверхностная плотность заряда, распределенного на поверхности .

Статические моменты поверхности относительно координатных плоскостей

, и :

∙( , , ) ,

∙( , , ) .

Координаты центра тяжести (0, 0, 0) поверхности :

∙ ,

∙ .

Моменты инерции поверхности относительно координатных плоскостей, , , относительно координатных осей , , и относительно точки - начала координат:

2( , , ) ,

(2 + 2)( , , ) ,

(2 + 2 + 2)( , , ) ,

+ =

( + + ).

Пример 3.5.

Для поверхности :

{

= 2

+ 2

- вычислить:

≤ 1

а) электрический заряд , если

поверхностная плотность заряда ( , , ) = = ;

б) массу , если поверхностная плотность массы ( , , ) = ∙ ,

= .

Решение.

( , ) = 2

+ 2,

′

′ = 2,

Здесь имеем:

= 2,

= √1 + 42 + 42 .

а) =

( , , ) =

= ∙( ) = ∙

√1 + 42 + 42 ;

область

представляет собой круг радиуса 1 с центром в начале координат (рис. 3.14).

Перейдем к полярной системе

координат:

= ∙

[ = ∙

]

= 2 + 2

= ∙

′ √1 + 42

∙ =

= ∙∫2

∫1

√1 + 42

∙ =

∙(1 + 4

= ∙8 ∫0

∫0 √1 + 4

= ∙

2∙

∙(1 + 42)

|10

(5√5

− 1)

Рис. 3.14. Иллюстрация к Примеру 3.5

б) =

( , , ) = ∙ =

= ∙

= ∙ (2 + 2)∙√1 + 42

+ 42

= [ = ∙ ] =

∙ = ∙∫2

∫1

∙ =

= ∙ ′ 2∙√1 + 42

2∙√1 + 42

= 1 + 42 2 =

− 1

] = ∙∫2

∫5

− 1

∙√

∙

= ∙

∙2∙∫5( − 1)∙√

= [

= 8 =

1 ≤ ≤ 5

= √

= 2

= [

] = ∙

∙ ∙∫1√5(2 − 1)∙22 = ∙

∙∫1√5(4 − 2) =

= 2 ∙ , 1 ≤ ≤ √5

5√5

10√5

2 + 50√5

(1 + 25√5)

∙(

−

) |√5

∙(5√5

−

) =

∙(

) =

∙

Ответ:

а) =

(5√5

− 1)

;

б) =

(25√5

+ 1)

3.3. Поверхностный интеграл 2 рода

Для продолжения изучения темы, связанной с поверхностными интегралами,

необходимо уточнить понятие стороны поверхности.

3.3.1. Сторона поверхности

Интуитивно кажется очевидным, что

= ( , )

у любой поверхности в пространстве есть две

стороны. Например, у поверхности, заданной

явным уравнением:

= ( , ) - есть

верхняя сторона и нижняя сторона (рис. 3.15).

−

Если поверхность задается уравнением:

= ( , ), то можно говорить о правой стороне

	и левой стороне; а если она задается уравнением:
	= ( , ), то можно говорить о ближней
		Рис. 3.15. К понятию стороны
	и дальней стороне поверхности.
		поверхности
	В случае, когда поверхность является

<<< < Предыдущая 1 2 3 4 5 6 78 / 138 9 10 11 12 13 > Следующая >>>

Соседние файлы в папке Экзамен

#
05.06.2021154.18 Кб9Вопросы к экзамену.pdf
#
05.06.202110.65 Mб20Все лекции.pdf
#
05.06.2021101.62 Кб7Дополнительные вопросы.pdf