Добавил:

pro100durachok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Высшая математика

Файл:

Все лекции

.pdf

Скачиваний:

Добавлен:

05.06.2021

Размер:

10.65 Mб

Скачать

☆

1 / 131 2 3 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Раздел I

Интегральное исчисление функций нескольких переменных

Введение

Данный раздел состоит из 4-х глав и содержит изложение материала, связанного с новыми типами интегралов: кратных, криволинейных и поверхностных. Обоснование необходимости введения этих новых понятий приводится в начале каждой главы путем постановки и решения задач геометрического, механического и технического содержания.

В первых трех главах изучаются свойства новых типов интегралов и методы их вычисления, а также приложения в различных дисциплинах.

Четвертая глава посвящена основным элементам теории скалярных и векторных полей. Свойства, характеристики и особенности этих полей изучаются с помощью кратных, криволинейных и поверхностных интегралов, введенных в начале этого раздела.

Глава 1. Кратные интегралы

1.1. Двойной интеграл

Множество разнообразных задач физического и геометрического содержания, возникающих при исследовании законов природы и функционирования технических систем, приводят к понятию двойного интеграла. Рассмотрим некоторые из таких задач.

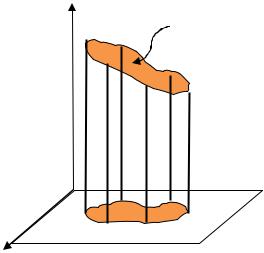
1.1.1. Вычисление объема цилиндрического тела

Введем понятие цилиндрического тела. Пусть задана функция = ( , ),

непрерывная в области 2 и ( , ) ≥ 0 ( , ) .
В системе координат рассмотрим тело T, ограниченное сверху
поверхностью = ( , ), снизу – областью на плоскости	и с боков -

цилиндрической поверхностью с образующими, параллельными оси (рис. 1.1). Такое тело будем называть цилиндрическим телом.

Найдем объем цилиндрического тела T.

Z = ( , )

Рис. 1.1. Изображение цилиндрического тела

Для решения этой задачи мы сначала

разобьем произвольным образом область

сетью кривых на частичные области ,

= 1, … , (рис. 1.2):

= … .

…

Далее рассмотрим цилиндрические

«столбики» с этими частичными основаниями ,

которые в совокупности составляют данное

цилиндрическое тело T.

При этом объем тела T будет равен сумме

объемов этих цилиндрических «столбиков»:

= + + … + =

∑

Разбиение области

где - объем - того цилиндрического «столбика». Рис. 1.2.

В каждой частичной области

выберем произвольно точку ( , )

1, 2, … , . Если «размеры» области

малы́, то можно приближенно принять

цилиндрический «столбик» за цилиндр с постоянной высотой

= (

)

= ( ,

Пусть ∆

= ( ) - площадь фигуры . Тогда ≈

∙∆

= ( )∙∆

≈ ∑

( , )∙∆ .

«Малость размеров» области определяется величиной ее «диаметра»

, где

= { ( , ): , } – максимально возможное расстояние между точками

этой области, а точнее:

= { ( , ): , } – точная верхняя граница

расстояний между двумя произвольными точками области ,

= 1, 2, … , .

Обозначим буквой λ ранг разбиения области , т.е. λ = {1, 2, … , }.

Тогда чем меньше значение λ, тем точнее приближенная формула для объема .

В пределе при λ → 0 получим точную формулу:

∑

( , )

∙ ∆

λ→ 0

Замечание 1.1.

Аналогично решаются и следующие задачи.

а) Вычисление массы неоднородной пластины (области) с известной поверхностной плотностью распределения массы ( , ):

=	∑	(	,	)∙∆
λ→ 0	=1

б) Вычисление электрического заряда пластины (области) с известной поверхностной плотностью распределения заряда ( , ):

=	∑	(	,	)∙∆
λ→ 0	=1

1.1.2. Понятие двойного интеграла

Пусть имеется функция = ( , ), заданная в области 2, где - замкнутая область, ограниченная гладкой (или кусочно-гладкой) кривой.

Выполним следующие действия.

1.Разбиение области на частичные области : = 1 2 … .

2.Выбор промежуточных точек: ( , ) , = 1, 2, … , .

3.Вычисление суммы: = ∑=1 ( , )∙∆ , где ∆ = ( ) – площадь частичной области , = 1, 2, … , .

Сумма называется интегральной суммой Римана функции ( , ) по области .

Заметим, что интегральная сумма зависит не только от значения , но и от

способа разбиения области на частичные области и от выбора промежуточных точек

( ,			) , = 1, 2, … , .

	Введем обозначения:
	– диаметр частичной области , = 1, 2, … , ; λ = { , … ,							}	- ранг разбиения.
							1
Определение 1.1.
	Число называется пределом интегральных сумм при λ → 0, если для > 0

> 0		такое, что для любого разбиения области с рангом разбиения							λ < и при
любом выборе промежуточных точек {					}		выполняется неравенство:
					=1
				\|		− \| < .

	Запись: = - означает, что при λ → 0 этот предел существует, он не
			λ → 0

зависит ни от способа разбиения, ни от выбора промежуточных точек, и равен числу .

Замечание 1.2.

Условие: λ → 0 - не равносильно условию: → ∞; условие → ∞ - необходимое, но

не достаточное условие для того, чтобы λ → 0.

Для введенного здесь нового типа пределов справедливы все свойства и теоремы о

пределах, рассмотренные в предыдущих разделах математического анализа.

Определение 1.2.

Конечный предел интегральных сумм

при λ → 0 называется двойным

интегралом от функции ( , ) по области .

Обозначение:

( , ) или:

( ) . Таким образом, по определению

имеем: ( , ) = ,

( ) = или:

λ → 0

( , ) = ∑

(

, )

∙ ∆

( ) =

∑

(

) ∙ ∆

λ → 0

Функция ( , ), для которой существует двойной интеграл, называется интегрируемой по области . Область называется областью интегрирования.

Пример 1.1.


0 = ∑=1		0∙∆ = ∑=1	0 = 0 = 0	0 = 0	.
	λ → 0	λ → 0	λ → 0

Геометрический смысл двойного интеграла.

Двойной интеграл: ( , ) , где ( , ) ≥ 0 ( , ) , равен объему цилиндрического тела T, ограниченного сверху поверхностью = ( , ), а снизу – областью на плоскости :

(T) = ( , ) .

Физический смысл двойного интеграла.

Двойной интеграл: ( , ) , где ( , ) − поверхностная плотность массы, распределенная по области равен массе всей области :

= ( , ) .

Двойной интеграл: ( , ) , где ( , ) − поверхностная плотность электрического заряда, распределенная по области равен заряду всей области :

= ( , ) .

1.1.3. Условия интегрируемости функции

Выясним условия (необходимые и достаточные) интегрируемости функций. Теорема 1.1 (необходимое условие интегрируемости).

Если функция ( ) интегрируема по области , то она ограничена в области .

Доказательство.

Пусть функция интегрируема, но не ограничена в области . Тогда при любом разбиении области на части - функция ( ) сохранила бы свойство неограниченности, хотя бы в одной из частичных областей .

В этом случае за счет выбора промежуточной точки можно сделать значение ( ), а значит, и значение интегральной суммы , сколь угодно большим.

Но тогда конечного предела существовать не может, т.е. функция ( ) будет неинтегрируемой. Это противоречит условию теоремы. Значит, функция должна быть

ограничена в области . Теорема доказана.

Обратное утверждение не имеет места: есть ограниченные, но не интегрируемые

функции.

Следствие 1.1.

Если функция ( ) не ограничена в области , то она и не интегрируема по этой

области.

Например, пусть = { ( , ): 2

+ 2 ≤ 1} - единичный круг на плоскости

, . Здесь = { ( , ): 2 + 2 < 1} - открытый

и функция ( ) = {

2 + 2−1

единичный круг, а = { ( , ): 2 + 2 = 1} - единичная окружность.

Функция ( ) не ограничена в области ,

т.к. ( ) → ∞ при , → .

Следовательно, функция ( ) не интегрируема по области .

Для получения признаков (необходимых и достаточных условий) интегрируемости

функций введем новые понятия.

Для произвольного разбиения { }

области введем следующие обозначения:

= { ( ), },

−

, = 1, … , .

Очевидно, что

≤ ( ) ≤

= 1, … , .

Величина

называется

колебанием функции ( ) в частичной области , = 1, … , .

Определение 1.3.

Пусть ∆

= ( ) - площадь частичной области , = 1, … , . Тогда величины:

= ∑

∙∆ и = ∑

∙∆

называются интегральными суммами Дарбу́- соответственно нижней интегральной

суммой и верхней интегральной суммой.

Очевидно, что для любого разбиения {

}

области и любого выбора точек

{

}

интегральная сумма Римана

находится между значениями интегральных сумм

Дарбу:

≤ ≤

Теорема 1.2 (основной признак интегрируемости).

Для того чтобы ограниченная функция ( ) была интегрируема по области ,

необходимо и достаточно, чтобы ( − ) = 0.

λ→0

Доказательство этой теоремы есть в работе [1].

Разность − можно выразить через колебания функции ( ):

− = ∑=1 ∙∆ − ∑=1 ∙∆ = ∑=1( − )∙∆ = ∑=1 ∙∆

В терминах колебаний функции ( ) основной признак интегрируемости можно сформулировать следующим образом.

Следствие 1.2 (основной признак интегрируемости).

Для того чтобы ограниченная функция ( ) была интегрируема по области , необходимо и достаточно, чтобы для > 0 > 0 такое, что для любого разбиения { }=1 области с рангом разбиения λ < и при любом выборе промежуточных точек { }=1 выполнялось неравенство: ∑=1 ∙∆ < .

1.1.4. Классы интегрируемых функций

Из основного признака интегрируемости можно установить классы функций, интегрируемых по заданной области.

Теорема 1.3.

Если функция ( ) непрерывна в области , то она и интегрируема по области .

Доказательство.

По условию теоремы функция ( ) непрерывна в ограниченной и замкнутой области . Следовательно, по теореме Вейерштрасса ([5], . . ) она ограничена в этой области, а по теореме Кантора ([5], . . ) она равномерно непрерывна в этой области.

Значит, для > 0 > 0 такое, что для любого разбиения области с рангом

разбиения λ < выполняется условие:	<		одновременно для всех = 1, … , .
		( )

Тогда ∑	∙∆	< ∑


=1		=1	( )

∙∆ = ( ) ∑=1 ∆ = ( ) ∙( ) = .

Итак, для > 0 > 0 такое, что для любого разбиения области с рангом

разбиения λ < выполняется неравенство: ∑=1 ∙∆ < .

По Следствию 1.2 это означает, что функция ( ) интегрируема по области . Теорема доказана.

Оказывается, интегрируемость сохраняется и для класса ограниченных функций, непрерывных «почти всюду» в области интегрирования.

Теорема 1.4.

Если функция ( ) ограничена в области и непрерывна в области всюду за исключением конечного числа точек или конечного числа кривых, лежащих в этой области, то она интегрируема по области .

Доказательство этой теоремы есть в работе [1].

Замечание 1.3.

Интегрируемость функции и величина интеграла сохраняются, если произвольным образом изменить значения функции в конечном числе точек или на конечном числе кривых, лежащих в этой области. Это связано с тем, что площади всех кривых равны нулю, поэтому соответствующие слагаемые в интегральных суммах не влияют на общую сумму.

Пример 1.2.

Вычислить двойной интеграл по квадрату :

= { ( , ) 2: 0 ≤ ≤ 1; 0 ≤ ≤ 1} (рис. 1.3).

Решение.

Здесь ( , ) = - непрерывная функция, значит, она интегрируема по области .

Следовательно, существует конечный предел интегральных сумм, не зависящий ни от способа разбиения области , ни от выбора промежуточных точек:

=					=	∑	∙∆ .
				λ → 0	λ → 0	=1


	Выберем удобное для нас разбиение
области и набор промежуточных точек.
	Разобьем квадрат вертикальными и
горизонтальными прямыми:
=		,	=	, , = 1, … , на = 2
=		,	=	, , = 1, … , на = 2

− 1

…			…
…			…
2


1


1	2	3		− 1
1	2	3	…	− 1	1
			…		1

Рис. 1.3. Область интегрирования

в Примере 1.2

равных квадратных ячеек со сторонами

(рис. 1.3).

Площади ∆ и диаметры этих ячеек имеют следующие значения:

= 1, … , 2.

∆ =

∙√2 ,

В каждой ячейке выберем в качестве промежуточной точки одну из вершин,

например, в правом верхнем углу:

≡

(

) (рис. 1.4).

Вычислим интегральную сумму:

= ∑

( )∙∆

∑

( )∙

, =1

∑

∙

∑

(∑

∙

) =

, =1

∑

∙(∑

) =

(∑

)∙(∑

) =

(

∑

)∙(

∑

) =

(1 + 2 + … + )2 =

− 1

1 +

(1 + )2

(

∙ ) =

− 1

, значит:

Здесь ранг разбиения λ = ∙√2

λ → 0 → ∞. Следовательно:

Рис. 1.4. Выбор

(1 + )2

промежуточных точек

λ → 0

→∞

Ответ:

1.2. Свойства двойного интеграла

Исходя из определения двойного интеграла:

( ) =

∑

( )∆

, или

λ → 0

( , ) =

∑

( ,

)∆ ,

λ → 0

выведем основные его свойства.

1.2.1. Свойства, выраженные равенствами 1. Нормированность.

Двойной интеграл от единицы по заданной области равен площади этой области:

= ( ) или: = ( )

2. Линейность.

Пусть функции ( ) и ( ) интегрируемы по области . Тогда

а) постоянный множитель можно выносить за знак двойного интеграла:

∙ ( ) = ∙ ( ) , = ;

б) двойной интеграл от суммы функций равен сумме двойных интегралов от этих функций:

( ( ) + ( )) = ( ) + ( ) .

Свойство линейности можно записать и в следующем виде:

	(1	∙ ( ) + 2	∙ ( )) = 1∙	( ) + 2∙	( )	1, 2 = .

3. Аддитивность.

Пусть функция ( ) интегрируема по области .

Если область интегрирования разбита на две области, то двойной интеграл по всей области равен сумме двойных интегралов по каждой из этих областей:

( ) = 1 ( ) + 2 ( ) ,

где = 1 2, 1 ∩ 2 = (или это пересечение состоит из конечного числа кривых).

Доказательство.

1. Нормированность.

= ∑ =1 1∙∆ = ∑ =1 ∆ = ( ) = ( ).

λ → 0

2. Линейность.

а) ∙ ( ) =

∑

∙( )∆

= ∙∑

( )∆

λ → 0

= ∙

∑

( )∆

= ∙

( ) .

λ → 0

б)

( ( ) + ( )) =

∑

( ( )

+ ( )) ∙ ∆ =

λ → 0

∑

( )∙∆ +

∑

( )∙∆

( ) +

( ) .

λ → 0

При этом установлено, что из интегрируемости функции ( ) следует интегрируемость функции ∙( ), где = , а из интегрируемости функций ( ) и ( ) следует интегрируемость функции ( ) + ( ).

3. Аддитивность.

Рассмотрим такое разбиение области на частичные области, чтобы линия пересечения 1 и 2 оказалась бы одной из линий разбиения области . Введем обозначения интегральных сумм Римана:

( ) = ∑		( )∙∆			- по области ;
=1
(1)( ) =	∑		( )∙∆ - по области ;
1		=1				1
(2)( ) =	∑			(	)∙∆	- по области .
2		= +1				2

Тогда имеем:

( ) = (1)(1) + (2)(2).

Переходя к пределу в этом равенстве при λ → 0, получим:

( ) = 1 ( ) + 2 ( ) .

1.2.2. Свойства, выраженные неравенствами

Пусть функции ( ) и ( ) интегрируемы по области .

1. Интегрирование неравенств.

Если ( ) ≥ ( ) ,			то и		( ) ≥		( ) .
Доказательство.
( ) ≥ ( ) ( )∙∆				≥ ( )∙∆		(т.к. ∆ > 0)

	∑	( )∙∆	≥ ∑		( )∙∆
	=1			=1

для любого разбиения области и любого выбора промежуточных точек { }=1. Переходя к пределу в последнем неравенстве при λ → 0, получим:

	∑	( )∙∆		≥	∑		( )∙∆			( ) ≥	( ).
λ → 0	=1			λ → 0	=1


Следствие 1.3.		Если ( ) ≥ 0			, то и				( ) ≥ 0.
Действительно:				( ) ≥ 0 = 0.
Следствие 1.4.		Пусть ( ) ≥ 0			; тогда для любых областей 1, 2
справедливо утверждение:
		1	2			( ) ≤			( )
					1			2

(т.е. с расширением области интегрирования двойной интеграл возрастает).

Действительно: 2 = 1 (2\1); 2\ 1 ( ) ≥ 0

2 ( ) = 1 ( ) + 2\ 1 ( ) ≥ 1 ( ) . Следствие 1.5. | ( ) | ≤ |( )|.

Действительно: −|( )| ≤ ( ) ≤ |( )| − |( )| ≤ ( ) ≤ |( )| | ( ) | ≤ |( )|.

2. Оценки двойного интеграла.

Если значения подынтегральной функции ( ) в области ограничены величинами и , то значение двойного интеграла ограничено величинами∙( ) и ∙( ), где ( ) - площадь области :

≤ ( ) ≤ ∙( ) ≤ ( ) ≤ ∙( ).

Действительно:

( ) ≥ ∙ = ∙ = ∙( );

( ) ≤ ∙ = ∙ = ∙( ).

Пример 1.3.

Оценить значение двойного интеграла:

=	1	, где
	100 + 2 + 2

= { ( , ) 2: | | + | | ≤ 10}.

Решение.

Область - квадрат со стороной 10√2

								2		Рис. 1.5. Область
(рис. 1.5) ( ) = (10√2)									= 200.
										интегрирования в Примере 1.3
	1		1				1
		≤				≤			( , )
102			100 + 2 + 2
						100
	1	∙200 ≤ ≤		1	∙200	1,96 ≤ ≤ 2.
102
			100

Ответ: 1,96 ≤ ≤ 2.

1.2.3. Теоремы о среднем значении

Следствием доказанных свойств, выраженных равенствами и неравенствами, являются так называемые «теоремы о среднем».

Теорема 1.5.

Пусть функция ( ) интегрируема по области ;

= { ( ), }; = { ( ), }. Тогда [ ; ]:

( ) = ∙( ).

Доказательство.

Согласно оценкам двойного интеграла имеем:

∙( ) ≤ ( ) ≤ ∙( ) ≤ (1 )∙ ( ) ≤ .

Введем обозначение: = (1 )∙ ( ) ; тогда получим: ( ) = ∙( ),

причем ≤ ≤ . Теорема доказана.

Теорема 1.6.

Пусть функция ( ) непрерывна в области . Тогда 0 :

( ) = (0)∙( ).

Доказательство.

Согласно теоремам Вейерштрасса и Больцано-Коши ([4], . . ) функция, непрерывная в ограниченной замкнутой и связной области, принимает все промежуточные значения между наибольшим и наименьшим значениями функции.

По Теореме 1.5 имеем: ( ) = ∙( ), где [ ; ], причемнаименьшее значение, а − наибольшее значение функции ( ) в области .

Следовательно, 0 : (0) = . Тогда получаем:

( ) = ∙( ) = (0)∙( ).

Теорема доказана.

Число = (1 )∙ ( ) - называется интегральным средним значением

функции ( ) в области .

1.3. Вычисление двойного интеграла

Вычисление двойного интеграла ( , ) начинается с выяснения вида области . Мы будем различать области «правильные» и «неправильные».

1.3.1. Правильные области

Определение 1.3.

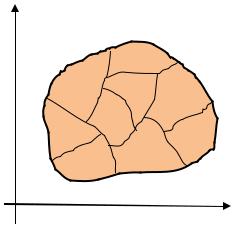
Криволинейная трапеция, ограниченная графиками функций = 1( ), = 2( ) (1( ) ≤ 2( ) [ ; ]) и прямыми = , = , называется областью, правильной в направлении оси .

Такие области характеризуются тем, что любая прямая, параллельная оси , пересекает границу области не более чем в двух точках (рис. 1.6).

Определение 1.4.

Криволинейная трапеция, ограниченная графиками функций = 1( ), = 2( ) (1( ) ≤ 2( ) [ ; ]) и прямыми = , = , называется областью, правильной

в направлении оси .

Такие области характеризуются тем, что любая прямая, параллельная оси , пересекает границу области не более чем в двух точках (рис. 1.7).

Y				Y
Y	= 2	( )
	= 2	( )

			= 1( )

	= 1( )				= 2( )
					= 2( )


			X
					X
Рис. 1.6. Область, правильная
	в направлении оси			Рис. 1.7. Область, правильная
				в направлении оси

Область может быть правильной и в направлении оси и в направлении оси .

Если область не является правильной ни в каком направлении, то такую область будем
называть неправильной.
Неправильную область, как правило,
Неправильную область, как правило,
можно разбить на части так, что каждая		3
из частей уже будет правильной в каком-либо	1	4
направлении. Например, кольцо на рисунке 1.8	1	4
направлении. Например, кольцо на рисунке 1.8
- неправильная область, но ее можно разбить		2
на 4 части так, что каждая из них уже будет		2
на 4 части так, что каждая из них уже будет
правильной в направлении оси .
Для правильных областей вычисление
двойного интеграла сводится к вычислению	Рис. 1.8. Разбиение неправильной
двойного интеграла сводится к вычислению	области на правильные
так называемых повторных интегралов,	области на правильные
так называемых повторных интегралов,
т.е. двух обычных (определенных) интегралов, взятых в определенном порядке.

1.3.2. Повторные интегралы

Пусть функция ( , ) интегрируема по области , где - правильная область в направлении оси , т.е. = { ( , ): 1( ) ≤ ≤ 2( ), [ ; ]}.

Справедливо следующее утверждение.

Теорема 1.7.

Если при любом фиксированном [ ; ] существует определенный интеграл

∫ 2( )	( , ) , то существует и повторный интеграл				∫	(∫ 2( )	( , ) ) , который
1( )						1( )
равен двойному интегралу:

		( , ) = ∫	(∫ 2( )	( , ) )				.
			1( )

Доказательство.

Доказательство теоремы проведем для случая, когда функция ( , ) непрерывна в области . Тогда, как известно, двойной и повторный интеграл существуют; в этом случае надо доказать лишь их равенство.

1 / 131 2 3 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в папке Экзамен

#
05.06.2021154.18 Кб8Вопросы к экзамену.pdf
#
05.06.202110.65 Mб17Все лекции.pdf
#
05.06.2021101.62 Кб6Дополнительные вопросы.pdf