
Теоретические основы теплотехники 1
.pdf
|
|
61 |
|
. |
|
. |
|
A |
A |
II |
|
|
I |
|
|
. |
|
. |
|
|
. |
|
. |
II
t |
I |
t |
II |
|
|
Рис. 13. Адиабатно изолированная система двух термически сопряженных тел
Первое и второе тело осуществляют разнообразные процессы измене-
ния состояния, к ним извне подводится (или отводится) работа, между тела-
ми происходит теплообмен, но для адиабатно изолированной системы вы-
полняется обязательное условие
Q Q |
Q |
I |
II |
0
.
(156)
Разделим уравнение (156) на некоторую функцию, зависящую только от температуры (t). Для идеального газа эта функция равна абсолютной температуре (tII) = TII . С учетом равенства температур двух тел получаем
Q |
I |
|
|
|
|
||
|
|
|
|
( t |
I |
|
) |
|
|
|
|
Q |
|
|
|
II |
|
( t |
II |
) |
|
|
|
0
.
(157)
Так как тела I и II возвращаются в исходное состояние одновременно
(согласно теореме теплового равновесия тел в равновесных круговых про-

62
цессах) последнее уравнение можно интегрировать по замкнутому контуру
|
Q |
|
|
Q |
|
||
|
|
I |
|
II |
|
||
|
|
|
|
|
|
||
|
( t |
I |
) |
|
( t |
II |
) |
|
|
|
|
|
|
||
0
.
(158)
Второй интеграл по замкнутому контуру для идеального газа, как ин-
теграл функции состояния, равен нулю
|
Q |
II |
dSII |
|
|
|
|||
|
|
|
|
|
|
( t |
II |
) |
|
|
|
|
||
0
.
(159)
Поэтому и первый круговой
нулю
интеграл
Q |
I |
0 . |
|
|
|
||
|
|
|
|
( t |
I |
|
) |
|
|
|
|
в уравнении (158) также равен
(160)
Если круговой интеграл равен нулю, то это значит, что подынтеграль-
ное выражение представляет из себя полный дифференциал некоторой функции состояния, названной энтропией ( S ), а функция (tI) является инте-
грирующим делителем
Q |
I |
|
Q |
I |
|
|
|
|
|||
|
|
|
|
||
( t |
I |
) |
|
T |
|
|
|
|
I |
|
|
dSI
.
(161)
Так как тело I - любое тело и свойства тел I и II независимы, получен-
ное выражение (161) распространяется на все равновесные процессы изме-
нения состояния любых систем. Выбранная функция (t), которая не зависит от вида тел, называется абсолютной температурой (t)= Т, а температурная шкала называется абсолютной термодинамической.
Таким образом, получаем математическое выражение второго начала термостатики - принципа существования энтропии и абсолютной темпера-

63
туры для любых равновесных систем
dS |
Q |
|
Q* Q** |
(162) |
|
T |
|
T |
|
и для 1 кг системы
|
q |
|
q |
|
|
|
* |
ds |
T |
|
|
|
|
|
q** T
.
(163)
Второе начало термостатики утверждает принцип существования эн-
тропии и абсолютной температуры как функции состояния любой равновес-
ной термодинамической системы, совершающей обратимые или необрати-
мые процессы.
Следствия второго начала термостатики
Следствия второго начала термостатики широко применяются в термо-
динамических расчетах и формулируются на основе анализа его математиче-
ского выражения (162), (163).
Следствие I. Совместное выражение первого начала термодинамики и второго начала термостатики позволяет получить дифференциальное урав-
нение термодинамики, которое связывает между собой все термодинамиче-
ские свойства веществ
T ds= c dT + du v dv T
p dv
|
|
dh |
|
= cp dT + |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
dP |
||
|
|
|
T |
v dp . (164)
Следствие II. Координаты Т - S являются универсальными координа-
тами термодинамического теплообмена.
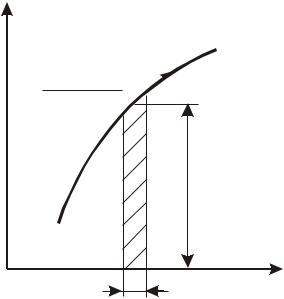
Рассмотрим процесс 1-2 в координатах Т-S и выделим на нем элемен-
тарный участок с температурой Т и изменением энтропии dS (рис. 14).
64
T
Q = T dS
 .
.
. 1
. |
2 |
|
T
d S |
S |
|
Рис. 14. Термодинамический процесс в координатах T-S
Исходя из математического выражения второго начала термостатики площадь под кривой элементарного участка процесса равна подводимому
(отводимому) количеству теплоты
Q = T dS. |
(165) |
При этом полное количество теплоты, подведенной или отведенной от системы в процессе 1-2, определяется следующим образом:
Q1,2 =
2 T
1
dS
.
(166)
Если из-под знака интеграла в соотношении (166) вынести среднюю температуру конечного процесса Tm , то количество теплоты в процессе мо-
жет быть определено по соотношению
Q1,2 = Tm (S2 - S1). |
(167) |
65
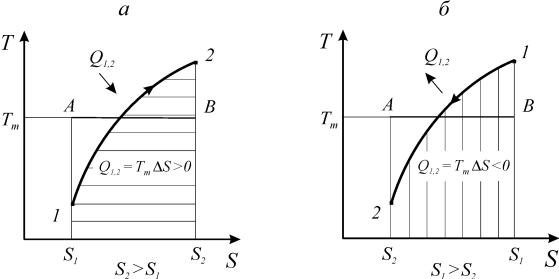
Как видно из выражения (166) и рис. 15, знак теплообмена определяет-
ся знаком изменения энтропии. Процессы, протекающие с увеличением эн-
тропии, сопровождаются подводом теплоты. Процессы, протекающие с уменьшением энтропии - отводом теплоты. Независимо от природы рабочего тела площадь под кривой процесса в координатах Т-S равна количеству под-
веденной или отведенной теплоты.
Рис. 15. Теплообмен в термодинамических процессах
Следствие III. Адиабатный процесс является процессом изоэнтропий-
ным.
Так как в адиабатном процессе теплообмен отсутствует ( Q = 0), то,
согласно второму началу термостатики (162), в таком процессе изменение энтропии dS = 0 (S = idem). Согласно этому следствию, показатель адиабат-
ного процесса ( k ) равен показателю изоэнтропийного процесса ( |
n |
s ) |
|
|
|
k ns . |
|
(168) |
Следствие IV. Коэффициент полезного действия и холодильный коэф-
фициент термодинамических циклов тепловых машин не зависят от вида
66
цикла и природы рабочего тела, а определяются лишь средними абсолютны-
ми температурами рабочего тела в процессах подвода и отвода теплоты.
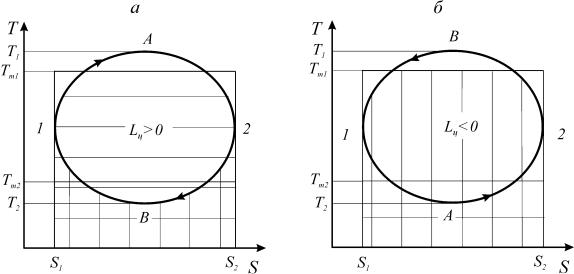
Рассмотрим термодинамические циклы в координатах Т-S: прямой цикл (цикл теплового двигателя) 1-А-2-В-1 (а) и обратный цикл (цикл холо-
дильной машины) 1-А-2-B-1 (б) (рис. 16).
В процессе 1-А-2 теплота подводится к рабочему телу. Количество подводимой теплоты соответствует на диаграмме горизонтально заштрихо-
ванной площади. Вертикально заштрихованная площадь соответствует коли-
честву отведенной теплоты от рабочего тела в процессе 2-В-1.
Рис. 16. Прямой и обратный циклы в координатах Т-S
Средние температуры рабочего тела в процессах подвода и отвода теплоты в цикле теплового двигателя обозначим Тm1 и Тm2
соответственно (рис. 16а). Согласно выражения (167), количества подведен-
ной и отведенной теплоты определяется по следующим соотношениям:
2 |
|
|
Q1 = TdS = Tm1 ( S2 |
- S1 ) = Tm1 S1,2 ; |
(169) |
1 |
|
|
67
Q2 =
2 TdS
1
= Tm2 ( S2 - S1 ) = Tm2 S1,2 ,
(170)
а коэффициент полезного действия любого термодинамического цикла теп-
лового двигателя может быть найден из выражения
1 |
Q2 |
= 1 |
Tm2 |
S1,2 |
=1 - |
|
|
|
|||
t |
Q1 |
|
Tm1 |
S1,2 |
|
|
|
||||
Tm2 Tm1
.
(171)
В результате аналогичных рассуждений получаем выражение для определения холодильного коэффициента термодинамического цикла холо-
дильной машины (рис. 16б)
|
|
|
Q |
|
2 |
||
|
|
|
|
|
t |
Q |
Q |
|
|
||
|
|
1 |
2 |
=
T |
S |
1,2 |
|
||
|
m2 |
|
|
|
|
( T |
T |
) S |
1,2 |
||
m1 |
|
m2 |
|
|
|
|
Tm2 |
|
= |
|
. |
Tm1 Tm2 |
||
(172)
Полученные выражения (171), (172) свидетельствуют о том, что КПД и холодильный коэффициент термодинамических циклов тепловых машин определяются только средними абсолютными температурами рабочего тела в процессах подвода и отвода теплоты.
Из уравнений (171), (172) следует также, что для любого термо-
динамического цикла тепловых машин выполняется следующее соотноше-
ние:
|
( |
t |
t |
|
1 )
1
)
.
(173)
Следствие V. Коэффициент полезного действия и холодильный коэф-
фициент цикла Карно всегда выше этих коэффициентов эффективности для любых других термодинамических циклов тепловых машин, осуществляе-
мых в одинаковом диапазоне предельных температур рабочего тела (T1 , T2 ).
Это следствие вытекает из анализа соотношений по определению КПД
68
цикла Карно (153) и любого термодинамического цикла (171) теплового дви-
гателя. Вследствие того, что Т1 >Тm1 и Т2 < Тm2 (рис. 16а),
K t
t
.
(174)
Аналогичный вывод можно сделать и при сравнении холодильных ко-
эффициентов обратных циклов
K t
t
.
(175)
Рассматриваемое следствие утверждает, что цикл Карно является эта-
лонным циклом, по сравнению с которым можно определить термодинамиче-
ское совершенство любого цикла, осуществляемого в заданном интервале предельных значений температур рабочего тела.
Следствие VI. Изменение энтропии системы равно сумме изменений энтропии всех тел, входящих в систему (теорема аддитивности энтропии).
Количество теплоты, полученное в элементарном процессе системой,
состоящей из r тел, можно определить из соотношения
|
r |
|
Q |
|
i |
|
Q |
|
|
i 1 |
|
,
(176)
что и подтверждает справедливость сформулированного следствия
|
Q |
|
1 |
r |
r |
Q |
r |
|
dS |
|
|
|
|
Qi |
i dSi . |
(177) |
|
|
|
|||||||
|
T T |
i 1 |
i 1 |
T |
i 1 |
|
||
Второе начало термодинамики и его следствия
Все явления природы, связанные с превращением энергии имеют необ-
ратимый характер. Обобщающим законом необратимости процессов в при-
роде является принцип возрастания энтропии изолированных систем. В ос-
69
нову второго начала термодинамики положен постулат, утверждающих не-
обратимость реальных процессов и имеющий ряд равнозначных формулиро-
вок:
теплота не может самопроизвольно передаваться от холодного тела к более нагретому (Р. Клаузиус, 1850 г.);
невозможно построить периодически действующую машину, вся деятель-
ность которой сводилась бы к выполнению механической работы и охлажде-
нию теплового источника (В. Томсон – Кельвин, 1852 г.);
любой реальный самопроизвольный процесс является необратимым
(М. Планк, 1926 г.);
работа может быть непосредственно и полностью превращена в теплоту путем трения или электронагрева.
Эти формулировки подчеркивают специфичность теплоты при ее пре-
вращениях. В теплоту полностью превращаются все виды энергии. Превра-
щения же теплоты всегда сопровождаются процессами, компенсирующими эти превращения. В тепловом двигателе такой компенсацией является пере-
дача некоторой части теплоты источнику низшей температуры (холодному источнику); в холодильных машинах такой компенсацией являются затраты работы.
Анализ различных формулировок постулата второго начала термодина-
мики приводит к некоторым весьма важным следствиям.
Следствие I. Невозможно осуществление полного превращения теплоты работу, т.е. нельзя создать вечный двигатель второго рода (Perpetuum mobile II рода) с коэффициентом полезного действия равным единице.
Это следствие вытекает из постулата в формулировке Томсона-
Кельвина, согласно которой всякий тепловой двигатель должен иметь как ми-
нимум два источника теплоты с различной температурой Т1 и Т2. Следова-
тельно, всегда Q2* > 0 и поэтому

|
70 |
|
|
|
* |
|
|
|
Q |
|
|
1 |
2 |
1 . |
|
* |
|||
|
|
||
|
Q |
|
|
|
1 |
|
(178)
Следствие II. КПД реального теплового двигателя и холодильный ко-
эффициент реальной холодильной машины, в которых осуществляются цик-
лы при температурах внешних источников Т1 и Т2 , всегда меньше КПД и холодильного коэффициента обратимых тепловых машин, циклы в которых осуществляются между теми же внешними источниками:
< обр ; < обр . (179)
Снижение КПД и холодильного коэффициента реальных тепловых ма-
шин по сравнению с обр и обр обратимой тепловой машины обусловлено прямым превращением части работы в теплоту (необратимые потери рабо-
ты) и наличием конечной разности температур между внешними источника-
ми теплоты и рабочим телом.
Следствие III. Абсолютный нуль по термодинамической абсолютной шкале температур (шкала Кельвина) недостижим (T 0 K ).
Это следствие вытекает из анализа соотношения по определению КПД цикла Карно (153) и постулата второго начала термодинамики в формули-
ровке Томсона-Кельвина. Поскольку КПД любого теплового двигателя и да-
же работающего по эталонному циклу Карно всегда меньше 1
К t
1 |
T |
|
2 |
||
|
||
|
T |
|
|
1 |
1
,
(180)
и в случае, если горячий источник теплоты имеет положительную темпера-
туру по термодинамической абсолютной шкале температур (T1 0 ),
справедливо утверждение
T2 0 . |
(181) |
