Теоретические основы теплотехники 1

21

Эти уравнения называются уравнениями Клапейрона – Менделеева.

Закон Джоуля определяет, что внутренняя энергия идеального газа за-

висит только от температуры

Отсутствие теоретически обоснованного единого уравнения состояния реального газа привело к выводу большого количества эмпирических и полу-

эмпирических уравнений состояния, справедливых для отдельных газов в ограниченном диапазоне изменения параметров их состояния.

Чем точнее уравнение, тем больше (как правило) оно содержит инди-

видуальных констант. Так, в известном уравнении состояния Ван-дер-Ваальса содержится две константы, а в более точных уравнениях число констант доходит до десяти и более.

В инженерных расчетах часто пользуются уравнением состояния иде-

ального газа с введением в него поправочного коэффициента (z), называемо-

го коэффициентом сжимаемости

Коэффициент сжимаемости (z) учитывает различие между идеальным и реальными газами (для идеального газа z = 1).

Коэффициент сжимаемости является функцией давления, температуры и зависит от природы газа.

Для обобщения данных по коэффициентам сжимаемости различных газов был использован принцип «соответственных» состояний, сформулиро-

ванный Ван-дер-Ваальсом. Принцип «соответственных» состояний утвер-

ждает, что критическое состояние действительно является одинаковым для всех веществ.

ковом удалении от критической точки.

Степень удаления от критической точки определяется с помощью приведенных параметров:

Уравнение состояния, записанное в виде F ( w, , ) = 0, называется при-

веденным уравнением состояния. Оно не содержит индивидуальных кон-

стант вещества.

Состояния вещества, в которых они имеют одинаковые и называ-

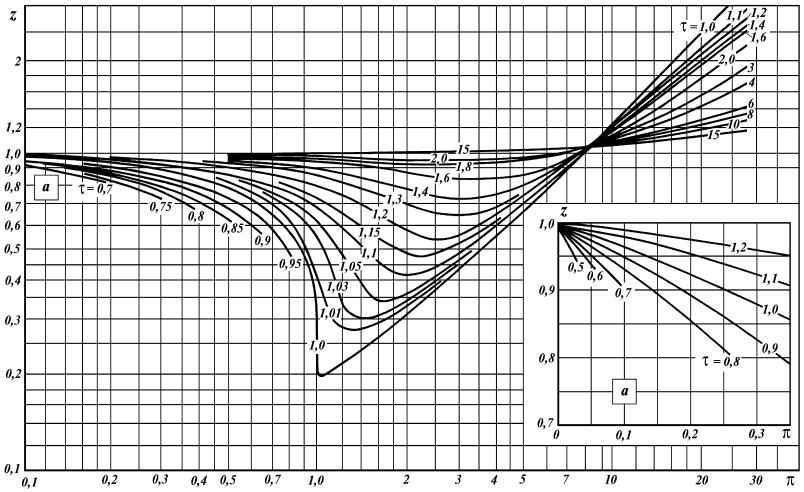
ются соответственными. Зная параметры и по данным рис. 4 определя-

ется коэффициент сжимаемости z.

Уравнения (35), (36), (37) являются математическим выражением пер-

вого начала термодинамики по внешнему балансу теплоты и работы.

В термодинамике приняты следущие знаки при определении работы и теплоты в уравнениях первого начала термодинамики: если работа выполняется телом, то она положительная; если работа подводится к телу, то она отрицательная. Если теплота сообщается телу, она имеет положительное

значение; если теплота отводится от тела, она имеет отрицательное значение.

преодоление сил трения, удары, завихрения превращается в теплоту внут-

26

Уравнения (40) и (41) называются уравнениями первого начала термо-

динамики по балансу рабочего тела, и справедливы для реальных процессов.

термодинамики по внешнему балансу и балансу рабочего тела совпадают.

Первое начало термодинамики для простых тел

Для простых тел, то есть систем, состояние которых определяется дву-

мя независимыми переменными, термодинамическая работа определяется как L p dV и математическое выражение первого начала термодинамики в дифференциальной форме примет следующий вид:

для термодинамической системы

для 1 кг системы

Выражение удельной потенциальной работы можно представить в виде соотношения

27

Поскольку энтальпия определяется с помощью параметров состояния

(u, р, v), то она является функцией состояния, а для простого тела может быть представлена в функции любых двух параметров, например, р и Т. Диффе-

ренциал функции состояния является полным дифференциалом и, следова-

тельно,

Подобно полной внутренней энергии энтальпия системы является экс-

тенсивным параметром, зависит от количества вещества и определяется по соотношению H h G.

Первое начало термодинамики для 1 кг простого тела по балансу рабо-

чего тела в дифференциальной и интегральной форме можно представить в следующем виде:

Математическое выражение первого начала термодинамики по внеш-

нему балансу в дифференциальной и интегральной форме имеет следующий вид:

28

термодинамики по внешнему балансу совпадает с выражением первого нача-

ла термодинамики по балансу рабочего тела.

Аналитическое выражение первого начала термодинамики

Значения удельных внутренней энергии и энтальпии простого тела од-

нозначно определяются двумя независимыми переменными и могут быть представлены следующим образом:

Изменения внутренней энергии и энтальпии простого тела, как функ-

ций состояния, в элементарных процессах являются полными дифференциа-

лами и определяются соотношениями

Соотношения (55) и (56) получены, исходя из анализа зависимостей

(19), (48), который показывает, что для изохорного процесса ( v idem) част-

ная производная внутренней энергии по температуре равна истинной изо-

29

хорной теплоемкости

а для изобарного процесса ( p idem ) частная производная энтальпии по температуре равна истинной изобарной теплоемкости

В результате подстановки выражений (55) и (56) в уравнение (48) и

разделения переменных получим:

Данное соотношение (59) называется первым началом термодинамики для простых тел в аналитической форме.

Выражения в квадратных скобках уравнения (59) в литературе часто называют калорическими коэффициентами, которые могут быть определены по формулам, полученным с использованием дифференциальных соотноше-

ний термодинамики,

30

Коэффициенты Джоуля – Гей Люссака ( Du ) и Джоуля-Томсона ( Dh )

реальных газов определяются по таблицам термодинамических свойств,

представленным в справочной литературе.

Первое начало термодинамики для идеальных газов. Закон Майера. Энтропия идеального газа

Идеальные газы подчиняются уравнению состояния Клапейрона pv RT и закону Джоуля, согласно которому удельная внутренняя энергия идеального газа зависит только от температуры

Совместное использование уравнения Клапейрона и закона Джоуля приводит к выводу о том, что удельная энтальпия идеального газа также яв-

ляются функциями только температуры

С учетом законов идеальных газов и исходя из соотношений (55), (56),

изменение внутренней энергии 1 кг идеального газа в элементарном и конеч-

ном (1-2) процессах находится по следующим формулам:

а изменение энтальпии 1 кг идеального газа в элементарном и конечном (1-2)