
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdfУраховуючимо: рiвняннÿ Øредин ера для електронно¨ задачi, ма¹-
|
|
|
|
X X |
ˆ 2 |
|
|
|
|
|
|
|
X |
|
|
|
||||||||
|
|
|
|
Pj |
|
|
|
e |
|
|
|
|
|
|||||||||||
нихДля спрощенняункцiях запису ми не випису¹мо ар ументи в кое iцi¹нт |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
+ En Cnϕn |
= E Cnϕn. |
|
||||||||||||||
|
|
|
|
n |
|
2Mj |
|
|
|
|
|
n |
|
|
|
|||||||||
|
|
|
|
j |
|
|
|
|
|
|
|
|
||||||||||||
|
тепер |
|
Cn |
, хвильових ункцiях |
ϕn |
òà åíåð iÿõ |
e |
|||||||||||||||||
øåìî |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
En. îçïè- |
||||||
|
|
|
явно дiю операторiв iмпульсiв ядер |
ˆ |
|
|||||||||||||||||||
хвильовi ункцi¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ϕn: |
|
|
|
|
|
|
|
|
|
|
|
|
Pj = −i~ j íà |
|||||||||||
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ 2 |
|
||||||
X X |
|
|
2 |
|
|
|
|
|
i~ |
|
|
|
|
! + Ene ϕn Cn |
||||||||||
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
Pj |
|||||||
|
|
|
|
− |
|
|
|
j2ϕn |
− |
|
j ϕnPˆ j + ϕn |
|
|
|||||||||||
|
|
|
|
2Mj |
Mj |
2Mj |
||||||||||||||||||
|
|
|
|
це рiвняння злiва на |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Помножимо= E Cnϕn. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
натами електронiв |
|
|
|
|
|
|
ϕn′ i проiнте ру¹мо за коорди- |
|||||||||||||||||
|
|
|
|
|
|
|
r1, r2, . . . : |
|
|
|
|
|
|
Z |
|
Z |
||||||||
n |
|
j |
|
|
|
Z |
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|||||
X |
|
X |
|
|
~2 |
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|||
|
( |
|
− |
2Mj |
|
dr1 |
|
|
dr2 . . . ϕn′ j2ϕn − |
Mj |
|
|
dr1 |
dr2 . . . |
||||||||||
|
|
|
|
|
|
|
|
|
|
ˆ 2 |
|
|
|
|
|
|
|
n |
|
|
|
|||
використалиˆ |
|
|
|
|
Pj |
|
|
e |
|
|
|
|
X |
|
|
|||||||||
|
òóò îðòîнормованiсть ункцiй |
|
|
|
||||||||||||||||||||
Ìè×ϕn′ |
j ϕnPj + δn′n 2Mj |
|
+ Enδn′n)Cn |
= E Cnδn′n. |
||||||||||||||||||||
Далi для зручностiZ |
|
Z |
|
|
|
|
|
|
|
|
|
ϕn: |
|
|||||||||||
dr1 |
|
dr2 . . . ϕn′ϕn = δn′n. |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
мiня¹мо мiсцями iндекси |
|
|
|
|||||||||||||
ми отримали |
аку систему рiвнянь: |
|
n i n′. Таким чином, |
|||||||||||||||||||||
|
|
|
|
X |
|
|
ˆ 2 |
|
|
|
|
X′ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Pj |
|
|
|
|
|
|
|
|
|
|
|
||||||||
682 |
|
|
|
|
|
|
+ Ene |
Cn + |
Vˆn,n′Cn′ = ECn, |
|
||||||||||||||
|
|
|
j |
|
2Mj |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
де оператор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íåâiäîìèõ |
|
|
Cn i |
|||||
åíåð i¨ |
X |
~2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
||
Vˆn,n′ |
= |
j |
− |
2Mj |
|
Z |
|
dr1 |
Z |
dr2 . . . ϕn j2ϕn′ − Mj Z |
dr1 Z |
|
dr2 . . . |
||||||||||
|
× ϕn j ϕn′Pj |
. |
|
|
äëÿ |
|
|
|
|
|
|
|
|
óíêöié |
|||||||||
Ця система рiвняньˆ |
|
|
|
визначення |
|
|
|
|
|
|
|||||||||||||
ктолив |
|
|
¹ чною. Якщо розглядати операт |
ˆ |
|
гаймера |
|||||||||||||||||
|
нульовому, так званому наближеннi |
|
|
|
|
||||||||||||||||||
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Борна Оппеяк збурення, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vn,n′ |
|
|
||
|
ˆ |
|
= 0, ми одержу¹мо систему незалежних рiвнянь: |
||||||||||||||||||||
|
Vnn′ |
||||||||||||||||||||||
|
|
|
|
|
|
X |
|
ˆ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Pj |
|
|
e |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Cn = ECn. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2Mj |
+ En |
|
|
|
|
||||||||||
Ми бачимо, що електронíà åíåð iÿ |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дiагоенер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ee |
|
|
|
|
|
|
|
|
i¨альнiдляядерно¨матричнiзадачiелементи.Наближення,n вiдiгра¹коливраховуютьсярольпотенцi ëüíî¨øå |
|||||||||||||||||||||||
|
|
|
|
|
îí. i |
óðàöiÿ |
|
ˆ |
|
оператора збурення, |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
Vnn |
|
|
|
|
|
|
|
|
|||||
ють адiабатичнимiвноважнак |
|
|
|
|
|
|
ÿäåð |
|
|
|
|
|
|
|
|
назива |
|||||||
âè ìiíiìóìó åíåð i¨ |
|
|
|
|
|
|
|
R0 |
, R0 , . . . визнача¹ться умо |
||||||||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
A |
B |
|
|
|
|
|
||
|
розкладом En |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
¹тьсями |
|
|
|
|
|
|
ункц. Урахування¨ коливних р хiв'язанихядер iйсню |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
e |
|
e |
|
|
|
|
|
|
|
|
|
|
|
¨õíiõ |
|
|
|
|
|
|
|
рiвноважних положеньó ðÿä |
|
|
||||||||||||
|
оординат вдоEn |
= En(RA, RB |
, . . .) |
uA = RA − RA0 , |
|||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
åíi÷íèõлектронно¨,i¨тоядерно¨сцмиляторiвприхпiдсистемидимо.. ТакЯкщозадаобмежитисьпричачiкдляжномузв'язу¹тьсясуêупностiвадранаборiточно,ичнимиквантовихз i длявiдхиленгарморiвнiвчисел |
|||||||||||||||||||||||
uB = RB |
− RB , . . . |
|
|
|
|
|
|
|
iльностi, |
|
|
|
|
|
|
||||||||
n å |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ee |
||||
|
|
|
|
задачi |
|
|
|
отриму¹м |
добре вiдомi вирази: |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
X |
~ωns(ns + 1/2), |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
E = |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
äå |
|
|
|
|
|
|
E = E − Ene (RA0 RB0 , . . .), |
|
|
|
|
||||||||||||
числаs нумеру¹ коливнi ст пенi |
|
|
|
|
|
ос иляторнi квантовi |
|||||||||||||||||
|
ns |
= 0, 1, 2, 3, . . . |
. Квадрати потенцiально¨÷ ñòîò êîë âàíü |
ωns |
|||||||||||||||||||
чаються |
звичайнимтобтододругихспособомх дних¹пропорцiйними доенеронстi¨ ви- |
||||||||||||||||||||||
жорсткостi,зна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
683n |
у положеннях рiвноваги, |
|
обернено пропорцiйними до мас ато |
|||||||||||||||||||||||
мiв.Умова застосовностi адiабатичного |
наближення поляга¹ |
|
ìà- |
||||||||||||||||||||||
лизнi середнього значення операторазбурення |
ˆ |
порiвняннi |
|
|
|||||||||||||||||||||
ðiçíèö ìè |
лектрон |
|
х енер iй. Середн¹ |
|
|
|
|
|
атора |
|
ç |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
значення опеу |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vn,n′ |
|
|
|
|
|
ˆ |
|
|
çà ïîðÿдкпараметром, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
величини дорiвню¹ |
|
i¨ коливань ядер |
|
|
|
Vn,n′ |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
адiабатичн |
|
наближення пр цю¹ за умови, що вiдношення~ω. Îòæå, |
|||||||||||||||||||||||
¹ малим |
|
|
|
|
|
лектронна енер |
iÿ |
|
|
|
~ω/Ee |
||||||||||||||
|
|
|
зведена |
|
|
|
|
|
|
Ee ~2 |
|
||||||||||||||
лiнiйнi розмiри молекули, ч стот |
|
ω |
p |
|
|
|
/ma2÷èìî,a |
||||||||||||||||||
нийщо малимзkâiäíEшення/a Mìàñè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
êîñòi |
|
e |
2 |
|
|
|
|
|
|
|
|
k/M , êîå iöi¹íò æ |
ñò |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
äðà |
|
|
|
|
|
|
|
|
молекуелектронатеорi¨рунтованиммасдоядерекулмаси.виступа¹Такимядра:чинмолекурiньм,дiабатичномикв |
|
|||||||||||||||||||
|
|
|
i¨ бертанняпаратром в e |
|
|
|
|
|
|
|
|||||||||||||||
муДля |
|
женнi рухiв¹вiдношеннялиенер |
|
|
m/M |
- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|||||
|
о ертових |
|
|
|
|
|
|
|
|
|
|
|
|
ω/E |
p2 |
|
|
|
|||||||
íàáë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
в личин |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
/I äî |
|||||
Оскiльк вiдношенняe |
2 |
e |
|
m/M , äå ìîìåíò iíåðöi¨ I |
|
|
M a |
2. |
|||||||||||||||||
|
|
E |
, тобто ~ |
/IE |
|
|
|
|
|
||||||||||||||||
òåорi¨ молекул ¹ добреŸ 87об. |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Молекусклада¹тьс, водню. адiабатичнеH |
наближення в |
||||||||||||||||||
|
|
|
|
|
|
m/M |
|
10− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ливу1981)моелектронннок,астðóõàéèаняхомамиЗапишемоаютьслераутíàùîîçãëрольiФтеорiю,мiжâóòâ.ÿâîдстанiËíåìîâäí¨îíäâiстядрзадачiþïîëiãàìiëüòîî,ютьякусистемуði¨íà,àìè(1900íàäâîквадлямолекупоклзапропонувалималих,iантово¨1954)основннерухщосистемалупочзадвiдстанях.вомехЦейднючiготокèõанiки(дивстанупiдхiд,вHÿäåðвантовiйпростома¹1927.. Íàñìîисвiдомий(протонiв),зроцi.лекузв'язаний68)цiкавäâîõдвома2хiмi¨.ВлиНа.електронiв,.теперiайтлеримеМиiзовiдiграввестанрозташоваðîçикихьякванимичасти(1904глянев'язокметодважвiдÿêi-
R = |RA − RB |
де гамiльтонiан першогоˆ |
електрона на ядрiˆ |
||||||
|
H = HA(1) + HB (2) + V , |
||||||
|
|
|
|
|
|
|
A |
|
|
pˆ2 |
|
e2 |
|
||
|
1 |
|
− |
|
|
r1A = r1 − RA, |
|
684 |
HA(1) = |
|
|
|
, |
||
2m |
r1A |
||||||
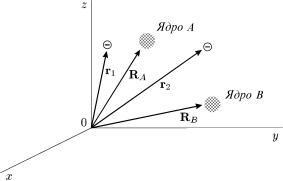
гамiльтонiанис. 68. Системадругогодвохелектронаелектронiвнауядрiполi нерухомих ядер A òà B.
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
pˆ2 |
|
|
|
e2 |
|
|
|
|
|
||
|
2 |
|
− |
|
|
|
|
|
r2B = r2 − RB . |
||||
Оператор |
HB (2) = |
|
|
|
|
, |
|
|
|||||
2m |
r2B |
|
|
||||||||||
|
ˆ |
|
e2 e2 |
|
e2 |
|
e2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V = |
|
|
|
|
|
|
величина), |
, |
||||
|
|
r + R − r1B |
− r2A |
||||||||||
|
|
|
|
|
r = r1 − r2, |
|
|
|
|||||
|
|
|
|
R = RA − RB |
|
||||||||
де перший доданок у ˆ |
|
|
|
|
|
|
|
|
|
|
âàííÿiдштовхудоданкиядерядер.- |
||
Хвильд угийовакулонiвськеннiйункцiязадачiенерелектронiвiяпрцеелектростцеяганняалаенерiяатичногоелектронiмiжелектронногоâдваiдоштовхуостаннчужих |
|||||||||||||
описую(ввання,елект |
|
V |
|
|
|
|
|
|
|
|
|
|
|
торових i спiнових змiнних |
ψ = ψ(x1, x2)залежить вiдспiновос |
||||||||||||
ункцi¨змперестановкиннаих,пртосторову,хвильова.Оскiлькиункцiягамiльтонiанзобража¹ться¹ антисиметричноюне добуткомвiд щодо-¨ |
|
¨õíüî¨ |
x = (s, r) |
òîìó |
нульовому наближеннi,ψ = χϕ. Миолицiкавимо основни станом, |
|
ˆ |
|
V = 0, просторову ункцiю685 |
|
|
óíêöi¨ |
|
ϕ двомарiзнихспособами, |
|
|||
амiльтонiабуду¹моiв з хвильових ункцiй, якi ¹ власними унк- |
||||||||
ϕöiÿìè= ϕ(ãr1, r2) |
|
êöiÿìè,ˆ |
ùîˆ описують.Отже,нехайелектрони |
|
|
|||
¹ хвильовими |
|
ò |
ϕ1s(r1B ) |
|||||
|
óí |
HA òà HB |
ϕ1s(r1A) |
|
||||
ядрах |
|
|
|
|
|
|
1s-ñòàíi íà |
|
A ò B, ê æåí |
ÿêèõ ì๠åíåð iþ E1s = −me4/2~2: |
|||||||
|
|
HA(1)ϕ1s (r1A) = E1sϕ1s(r1A) |
|
|
||||
емодвочаствихсиметризуватиункцiйову.Тут,ункцiюнавiдмiнуяк симетрвiд в зованийдкуатомадобутокHe, |
||||||||
мицУтворимохОтжхвиль |
|
HB (2)ϕ1s (r2B ) = E1sϕ1s(r2B ). |
|
|
||||
дноелектроннiе, |
|
|
центрованi на |
ядрах. |
|
îñêiëüêè |
||
де стала ϕ = C{ϕ1s(r1A)ϕ1s(r2B ) ± ϕ1s(r2A)ϕ1s(r1B )},
C визнача¹ться з умови нормування
ZZ
i ма¹ вигляд: ϕ (r1, r2)ϕ(r1, r2) dr1dr2 = 1
Величина |
1 |
. |
|
|
||
C = |
|
|
|
|
||
p |
|
|
|
|||
2(1 ± S2) |
|
|
||||
S = |
Z ϕ1s(r1A)ϕ1s(r1B ) dr1 |
|
|
|||
ма¹ назву iнте рал перекриття . Замi ою змiнних iнте руван я |
||||||
r = r1 − RA |
переходу дорiвíю¹ одиницi) |
|
||||
звести до вигляду(якобiан |
|
|
|
|
|
éîãî ìîæíà |
Iнте рал перекриттперекриваннязалежить вiдмiж'ядернихвiдстанi я рами |
||||||
S = |
Z ϕ1s(r)ϕ1s (r + R) dr. |
|
|
|||
причому |
|
|
|
|
|
S = S(R), |
S(0) = 1, на великих |
âiäстанях S(R) → |
|||||
0Îòæå,, îñêiëüêè |
хвильових ункцiй ¹ зникаюче малим. |
|||||
686 0 ≤ S(R) ≤ 1. |
|
|
|
|
|
|

ня повнЗа дîпомогоюамiльтонiанахвильово¨системи:ункцi¨ ϕ знаходимо середн¹ значен-
|
|
|
|
ˆ |
|
||
Простi обчислення приводятьE íàñ= hHäîi. такого результату: |
|||||||
де кулонiвський iнте ралE = 2E1s + |
K ± A |
, |
|
||||
|
|
|
|
|
1 ± S2 |
|
|
|
iíòå ðàë |
dr2 |
|
ˆ |
|
||
à îáìiííèéK = Z |
dr1 Z |
ϕ1s(r1A)ϕ1s(r2B )V ϕ1s(r1A)ϕ1s(r2B ), |
|||||
|
Z |
Z |
|
|
|
|
|
Öi |
величини очевидноiнтеакожна¹ ункцiямиˆ |
мiж'яде но¨ вiдстанi: |
|||||
A = |
dr1 |
dr2 |
ϕ1s(r1A)ϕ1s(r2B )V ϕ1s(r1B )ϕ1s(r2A). |
||||
числовихобчисленнiнихKвиснажливих=ÌèKóíêöié(R),ç Aобмiнного.водимочень=Пода¹моAрозрах(.R).òˆõóостаточнийнкiвмоцихрала,.Найбiльшiнескладних,обчислитиякийрезультрузводитьсяат:аледнощiовестидоволiвиникаютьдорезугроелементль iздкихатиприардо-
|
S = e−ρ 1 + ρ + |
ρ2 |
, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
äå ρ = R/aB, C = 0.57722 стала Åéëåðà, |
|
|
|
|
|
|
||||||||||||||||||||
|
e2 |
|
e−2ρ |
5 |
|
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
K |
aB |
= |
|
ρ |
1 + |
8 |
ρ − |
|
4 |
ρ2 − |
6 |
ρ3 , |
|
|
|
|
|
|
|
|
||||||
A |
e2 |
|
S2 |
6 |
(C + ln ρ) + e−2ρ |
11 |
|
103 |
|
49 |
|
11 |
|
|||||||||||||
aB |
= |
ρ |
1 + |
5 |
8 |
+ |
20 |
ρ + |
15 |
ρ2 + |
15 |
ρ3 |
||||||||||||||
|
|
+ |
6 S1 |
[S1Ei(−4ρ) |
− 2SEi(−2ρ)] |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
5 ρ |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ei(x) = − Z−x dy e−y /y |
|
|
|
|
|
687 |
|||||||||
iнте ральна показникова ункцiя i |
|
|
|
|
|||||||||
|
|
|
|
|
ðàë, |
ρ |
− ρ + ρ |
2 |
/3). |
|
|
||
величиною,Кунiвський iнте S1 |
= e (1 |
|
|
|
|||||||||
äiãð๠|
îáìiííèé |
|
|
âiä'¹ìíîþKякиймалимудiлячислом,цiмалихмiнiмумомголовну роль вi- |
|||||||||
|
|
à ïðè |
|
|
|
|
|
|
|
|
R ¹ äîäà |
||
|
|
|
|
|
R = a aB змiню¹ знак. Причому сума |
||||||||
K + A äëÿ R > a ¹ |
|
|
|
величи ою |
þ |
òî÷öi |
|||||||
R0 1.51aB |
= 0.80 A |
|
рiзниця K − A ¹ дода |
|
|||||||||
для вс х значень |
|
|
|
|
|
|
|
|
|
|
величиною |
||
|
i |
|
R |
. Таким ч ном, для иметричíî¨ просторово¨ |
|||||||||
у кцрично¨ |
|
|
|
|
|
(дивункцi¨мiж.ядрамирисстзв'язаного.69)системи. Експериментальнетеорiя айтлераз |
|||||||
ченняЛо донарiвϕда¹оважно¨можливимякiнийвiдстописзв'язаний |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
ункцi¨гелiю, ригадаймо,ст нущонема¹симетричнiй. Для.Тепер,анти |
|||||||
|
|
|
|
рi¨ово¨атома |
|
|
|
|
|
||||
|
|
|
îâié |
|
|
|
|
|
|
|
|
||
|
|
ñòî |
|
|
|
|
|
|
|
|
|
||
|
|
òå |
|
|
|
|
|
|
|
|
|
|
|
èìå |
досвiдхвильпроз |
|
|
|
|
|
|
|
R0 = 0.74 A |
|
|||
просторовiймаючи |
|
|
|
|
|
|
|
|
|
|
|||
пiноваан,спiном,йогоункцiя,познарiвнимчаютьякнулевiопису¹як.Успiцьомуовийвiдвипадкуовiст а¹двомиднхìà¹ìîелектронiвнтисиметричнасинлетнийiз пов |
||||
íèì |
ϕ |
|
|
|
êöi¨ |
1Σ. Ан имет ичнiй простор |
óíê |
||
|
|
|
|
- |
|
ïîâiдаюнимнаòспiном,вiсьтрисиметричнiiвнимдиницi,спiнîâiтрьома |
|||
можливимицi¨, якiϕ якописуютьмипроекцiямизна¹стано,вiдiзспiну |
|
|
|
|
|
|
триплетний стан 3 |
|
|
атомипритягуютьсяводню,цьогоякийелектрхiмiчноговизнача¹тьсйутворюютьнизв'якихзкухвильовоюаютьмолекулида¹аналiзпротилеж.óíêöi¹þЯкiсрозпо. е |
||||
дiлупояснапрямленiОтже,густиниеннядвавиникненняспiни,електронiв, |
z |
|
|
Σ |
ϕуваннязображенийелектронiвгра посерединiiчнонарисантисиметричногомiж.69. ядрами,Якбачим ,лиiмовiрнiсть пере
симетрич |
о¨ хвильово¨ ункцi¨ |
2 |
|
|
r1A = r2B , äëÿ |
||
áiльшоюункцiя. Навпаки,цiйу точцiвипадкуоберта¹тьс |
â íóëü, |
|
|
2 |
|
||
|
|
розв'язку найхви |
|||||
льова |
ϕ = 2ϕ1s(r1A)/p2(1 + S ) |
|
|||||
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
- |
вiдштовхуванняшепершомуперебудiлянккулонiвськогозв'язкуакийутвсистемуипадкуютьюреннярухмiж.вiмiжЦеäелектронiв,воелектрони,iгра¹молекуядрамивiдштовхуванняядрами¹атомiвпринциппр.чиною.Приi.АнткомпенсуютьколрухаючисьВизнацьПаулi,âоничальнуiжетрична, кненняякийзрозуперебуваютьядрамисилирольдозволя¹кiйхвильоваiло,зв'язаного¨хсистеммипереважутвореннiлонма¹мо.перебуваОтже,iвськ,ункцiячастiаютьжогонехiв |
|||||||
мiчногозв'язанусилипозаопису¹атомiв |
|
|
|
ϕ = 0 |
|
|
|
688 |
|
|
|
|
|
|
|
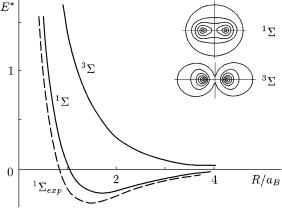
èñ. 69. Åëåêтроннi |
терми |
ìî êóëè |
водню. Суцiльнi |
ëiíi¨ |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р я айтлера Лондона для син ëåтного тНатриплетного станiв, Eòåî= |
|||||||||||||
(E 2E1s)/ e2 |
; øòð õîâà åê |
|
|
. |
|
вставцi зображено розп - |
|||||||
електронно¨2 |
ãóñòèни для термiвсперимент |
|
|
|
|
|
|||||||
äië− |
aB |
|
|
|
|
1 |
|
à 3 |
|
|
|
|
|
пчином,тиротилежнiзподiломр лярнихобомМолекуликванелектронамметозхiмiчнихлаелектронiвнапряаквалентностi,воднюзваниммеханiксполуккимiжлера¹зовнiшнайпростiшимвза¹мноядрамипiдахЛалевнiстюреалiзу¹тьсятнимихкомпенсуютьслишеоболонокрозумiютьз'яхiмiчнимîñíîтодi,прикладом.âйоннийаламiжолизв'яприро.¨хнiатомами |
|
|
|||||||||||
|
|
|
|
|
|
|
Σ |
|
Σ |
çгв'язокдуспiниеополярн.хiмiчногоУ.iзгетмаютьТакимåðîå¨ |
|||
çâ'ÿçêó |
|
|
àéò |
|
íä íà ¹ |
|
|
îþ êâ íò âî¨ òå ði¨ |
|||||
îïî ÿðíî¨ |
|
сполучатись iз |
ÿê |
|
|
|
|
атома д |
|||||
ìåíòiâ. |
емент |
|
|
|
êiëüêiñòþ àòîìiâ iíøèõ |
|
|||||||
хiмiчного зв' |
|
ùî ðîëü |
пiнових ступенiв вiльнос |
â óòâ ðåííi |
|||||||||
çêó |
ëÿã๠ñàìåпевноюдозволi перебува |
|
åëåê |
||||||||||
ðîí |
ìiæ ÿдрами. Мiж iншим, хiмiч ий зв'язок мiж атîìà |
||||||||||||
можПiдкреслимо,бути реалiзований не лише електро ами, але й iншиобом |
|
÷àñ- |
|||||||||||
òèíêàìи, наприклад, мюонами, |
|
¨õíi |
ñïiíîâi |
¹ ðiçíèìè |
|||||||||
(мю-мезоннi |
|
|
ëè). Òå, ùî ðîëü ñïi |
ово¨ змiн о¨ електрона |
|||||||||
не ¹ iншою, iлюстру¹молеку iснуванняякщомлекулярногоздатнiстьйоаниводню H+, хiмiчний44 I. О. Вакарчукзв'язок якому здiйсню¹ дин електрон. Теорiю молеку6892 -
лярного йона водню H+ ми розглянемо наступному парагра i. |
||
i НеможливiстьВiдступ. |
утворення2 |
молекули водню в триплетному альст |
3 |
|
|
|
|
|
|
òÿêå,ùî íдослiдженнязнайшлаенерзв'язаногозмовеликихуючисужутьцiкавеупнiснаслiдкiвелеквiдутворитизастосуванрони,ьаляхатомiвпри(спрмолекулетногосиламиципуямводнюлявут¹прямоговото¨хвипадкусильнежностiюспiни.Хочаекспермагнiтнездовжстслабкментнокполя.приЯке, |
||||||
íяганоговоΣпомiститиполяри |
|
|
|
|
|
|
iñíó¹ ç |
i¹þ |
|
4 A) |
|
атомамтомарний |
|
|
|
ñèí |
|
ìiæ |
â öü |
ñòàíi |
|
çðiäæóK ( |
|
ñò |
нер iя притяг ння |
||
|
5◦ |
|
|
|
|
|
ператури, |
|
|
|
|
||
çîâ |
|
|
|
|
|
|
áелекi¨явищепечунувiдомо,- внаслiдокденьбозеK)основномуоливань,-.айнштайнiвсько¨водню,-неВоногазперебува¹станувиямало¨зумовленестанiоскiлькиля¹.¹тьсмасияскравимОтже,виявдорiвню¹цiкстнавiтьанiкповниймвутомаонденсацi¨,цьомуiзикiввластивiсть:iмпульсами,прикладомнулевiспiнВвеликогоàíабсолютному.атомаАåоликвантовогоВрiвнимизначеннямакроскньомуми(протональсаотрима¹монулiпринциполяриiнулевiопiчнанеенерплюсжлигазуза |
||||||
|
нийгазрон)¹атомiвихатомiвбозе |
|
|
|
||
веЯккiлькiсть 4 |
|
|
|
-. |
||
5.5 |
× 10 ◦ |
|
|
|
|
|
Áîçå- |
нденсат ¹ чу |
ì |
|
ква товомеханiчного |
||
ïó òîòîжностi |
частинок |
|
ìàêðîскопiчних масштабах. Це явище |
|||
диву¹ як iзикiв-теорет |
êiâ, òàê |
-експериментаторiв, якi |
||||
тривалийатомарнийчасполяризованийŸдослiджують88. Молекулярниййоговоденьнатаких.йон воднюсистемах,H як рiдкий 4He
+
склада¹тьсЗапишемоньомупринципщомулюватиномвiнмiжозгполiдозволя¹лянемодвомасуперпосуть.Цюгамiльтонiандвохзадачуядрамгомеополярнсистемуçицi¨доспротонiв(Ÿ3,тьводмиПрикладнайпростiшуелектронно¨ювжстимго.зв'язкуелектрона,розглядматем2). Прикладзадачiмолекуяктиобмiняк,нимлярнуолийцейаналiзомруха¹ться2днимобговорюцiкавийсистемуелектросâтим,алиорщо¨х-
|
ˆ |
pˆ2 |
e2 |
e2 |
e2 |
||||
690 |
H = |
|
− |
|
− |
|
+ |
|
, |
2m |
|r − RA| |
|r − RB | |
R |
||||||

åПознал |
|
R = RA − RB . |
|
|
|
|
|||||||
åктронаi¨чåлектрона,ннядоочевиядерäванi:наступнiперший доданкулонiвськстороваоператоренерiя притяганнякiнетично¨ |
|||||||||||||
|
|
|
|
|
|
|
Пренеромбiнацi¹юiя вiдштовхуванняхвильовахвильовихункцiямiж- |
||||||
кцiйвядраминульовомуелектрона.ДослiдимонаближвAосновнийеннiBанi,¹остлiнiйноюаннiйст. |
|
|
|
|
|
||||||||
причому |
|1si-ñò |
|
центрованих |
|
|
ядрах A |
B: |
||||||
|
|
|
|
|
|
|
|
|
|
óíêöi¨, |
|
||
ϕ = CAϕ1s(rA) + CB ϕ1s(rB ), |
|
||||||||||||
rA = r − RA, |
|
|
|
rB = r − RB |
|
||||||||
електронабуваннязнеЗверта¹мопринципуставимоелектронаувагупитан |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|CA| |
+ |CB | = 1. |
|
|
|
|||||||||
|
тотопротæíÿàîнiте,простiаоднакщочастиноксиметрiюми ма¹моих.Охвильово¨яäймовiрдноелектроннунàх.iсIм ¹вiрнiссиме ьрiяякзадаперебуваннящодовиплива¹чу,тому- |
||||||||||||
протонi |
A äîðiâíþ¹ |
|
|
|
|
îñòi éîãî |
|
||||||
|
B: |
|
|
|
|
|
|
|
|
|
|
|
|
Îòæå, |
= ±CA |
|CA|2 = |CB |2. |
|
|
|
|
|
||||||
CB |
|
|
|
|
|
|
|
|
|
|
|
|
|
замiни знакнормуванняперед(iншiхвильрозв'язкиовоюункцi¹ю)зводяться.Такимлишечином,донесутт¹во¨ |
|||||||||||||
умови |
|
|
äèìî: |
|
|
|
|
|
|
|
|||
|
ϕ =çíàõC[ϕ1s(rA) ± ϕ1s(rB )], |
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|||
де iнте рал перекриття |
C = |
|
|
|
, |
|
|
|
|
||||
p |
|
|
|
|
|
|
|||||||
2(1 ± S) |
|
|
|
|
|||||||||
|
тепер середн¹ значення енер i¨ в станi |
|
|||||||||||
ОбчислимоS = Z ϕ1s(rA)ϕ1s(rB ) dr = |
Z ϕ1s |
(r)ϕ1s(r + R) dr. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ϕ: |
|
44* |
E = Hˆ |
i |
= E |
+ |
K ± A |
, |
691 |
||||||
|
|
h |
|
|
1s |
1 |
± |
S |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
