Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B

E , E

м ожники Ла ранж . Якщо ж прирiвняти до нуля

ˆ

δψ , δψ

,

ìè î

îã

ëü

,

[H0(1)

− Ef1 ]ψf1 (x1) + Vf2f2 (1)ψf1 (x1) ± Vf2f1

(1)ψf2 (x1) = 0,

-

J вiдриву iç системи частинки зi

àíó ψ

íàçâiìî ¨¨

ˆ

− Ef2 ]ψf2 (x2) + Vf1f1 (2)ψf2

(x2) ± Vf1f2

(2)ψf1 (x2) = 0,

[H0(2)

Vf f ′(2) = Z

Ef1 Ef2 . Для цього обчислiмо е

iþ

äå

dx1 ψf (x1)V (1, 2)ψf ′

(x1),

множникиf1 f2 бiля незалежних варiацiй

систему

iвнянь для спряжених ункцiйf1

ористоf2

ðèìà¹ìî

ψ

ψ

.

Îðñò енервдŸ10рт.

оюiстьЗ'ясуймопроцедуроюдежанихмiстортогоналiзацi¨,величинункцiйзабезпечу¹моякусистемидобревикf1

f2

вiдомоюували

àðòði Ôîê

¹þf1 éîíiçàöi¨. Äî éîíiçàöi¨ åíåð iÿ

äîðiâíþ¹f1

ˆ

éîíiçàöi¨

hHi, à ïiñëÿ

(0)

ψf2 (x2)Hˆ (2)ψf2 (x2) dx2.

Таким чином,

Ef2 = Z

Тепер перше

рiвняння

(0)

ˆ

à

помножмо

íà

системи

Jf1

= Ef2 − hH .

ψf1 (x1) i ïðîiíò

руймо за x1:

(0)

− Ef1 + Z dx1 Z dx2 ψf1 (x1)ψf2 (x2)V (1, 2)ψf2 (x2)ψf1 (x1)

Ef1

± Z

dx1 Z

dx2 ψf1 (x1)ψf2 (x2)V (1, 2)ψf1

(x2)ψf2 (x1) = 0.

Отриманийтонiана:

вираз можна записати через середн¹ значення гамiль-

ˆ

(0)

672

hHi − Ef2 = Ef1 .

Çâiäñè

находимо, що

ψ(1)

, ψ(1)

Отже, змiст множникiв

ранжа

Ëà−Ef1

= Jf1 .

дорiвнюють з оберненим зн

êîì åíåðEi¨ йонiзацi¨поляга¹ частинкивтому,Спочаткщозiствоíè

f

ψf

ó

ψ(0)

ψ(0)

i обчислю¹мо матричнi елементи

f1

f2

ження

еличин

Vf f ′

Vf f ′. Маючи

нульовi набли-

процедурухвиль

пiдставля¹мо ¨х

рiвняння, з яких знахонуди

повторю¹мåííi,óíêöi¨

,

öåñ

другомуорт гоналiзацi¨:обчислю¹моf1 f2 знайден

меншоюïðî

iтерацiйнийх елементиункцiй.Пiсля цього

матрич

льовихЗвiдси¹мо,наближункцi¨напередпокиункцiйрiзадано¨ниця¨х

Vf f ′

óçãîдимоцесстанедженняупродовжупершохвильхвивiу

наближмiжьоювеличинисудопомогоюсiднiми..ТобтоЦейнаближздорiвняповногоямиьзнахпрне

ìî

сисхви,

полемяк

Vf f

′

ψf1

ψсамоузгоf2

ìакихетодух,методелементiвякФокŸ 85бiартрiгромiздкими.ем,да¹ьМетоîâi. СучаснiелектронiзмФок,ункцi¨джгутТоми,ак.зíмасажайтиомп'юогопрак,молекули,,тверякполярозв'язкиФермiсамоичнодихери. значнотiлзалежитьувсiхтому.рiвнянняСамеатомiвзбiльшуютьчислiцимвiдперiоШренихдлям-.

систеiîназвастiзрахованiляартрi

складн

òдично¨акихдомжливМетоера

ßêùî

ма¹ багато

то обчисл

ìåòî

задачi

атома,

Па лi, електрони

âèìàã þòü

õ

âåëè

àþòü

¹

øèé

ïî

тужнихартрi Фок

ï'þòåðiâ. I

åíèé ìå д для багдом-

електронних

ñòîìiâ, ùî

ру ту¹тьсянаближтак званiй

моделi

ÿêó

1927 1928 р к х атистичнiйЛ. Томас

êèìè

вантов ми

чис самиФермi)отже, дляперебуваютьопису акî¨

истеми

ìîæ-

У цiй (моделi вваж ¹ться, що, внаслiдок багат ч стинковостi

Å. Ôåðìi

äåëü Òîì

ëàсичний

.

. Нехай ми ма¹мо систему з

íà

застосуватпринципу

E

електронiвбути постiйноюточкувеличиною, на

ше вiдбувався б пе

îâèäiëííà

iяотже,мiнiмальною. Вва-

æà¹ìî,

що акий пере озподiлнезв'язанийЗвiдсиr бувсвиплива¹,енерзалежнiсть

чином,чокмувелвипадкупросторучинами.Кмалиðiì òîãî,á åíåð iÿ ïî

наелектронбутивеличинуд'¹мною.Такимдля.

всiхiншзабезпечитВ

E = const

ìîâókF залежитьвектора,r i öÿ

¹ àêîþ, ùîá

òðîíiâ

E = const.

що густина елек-

ρ ¹ íêöi¹þ ðàäióñ-

ρ = ρ(r). Уведемо

Φ0

674

eΦ0 = E,

Нагада¹

~2

2

2/3

|e|(Φ − Φ0).

о, що заряд електрона

2m

(3π ρ) =

e = −|e|. Визначимосиметричдiуатома

R

умови

, тобто з рiвня ня

Φ(R) = Φ0

ρ = 0

зовнiшньелектрîнiвгополясерично.i Якщо- àòîì ¹éîíiâèåé-,

òоральнитаксистемарозподiлнестворю¹густини

iз зарядом

Φ0 = 0. Äëÿ

знах дження потенцiалйона

=¹ такою:Q/r ïðè r > R. I отже, умова

äëÿ

Q ðîçìiðiâ

Φ0

Q

Надалi ми будемо розг ядатиΦ(R) =íåéтральний.

àòîì, êîëè

R

Самоузгоджений потенцiал

Φ0 = 0.

ронами

густиною

Φ, що ств рю¹ться атомними елект-

джений потенцiал

ρ i

Φ. З вихiдного рiвняння

знаходимо

~2

(3π2ρ)2/3 + eΦ = 0

2m

â ðiâíÿíρ = 3π2

~2|

|Φ

,

яке пiдставля¹мо

íÿ Ïóассонà:

розглядуΔΦ = −4πe 3π2

~2| |Φ .

3/2

Уведемо до

óíêöiþ

χ = χ(r) спiввiдношенням

43*

Φ =

Z|e|

χ

675

r

r| |

dr2 =

3π|2

|

~2

r

.

Уведемо безрозм

ðíó

ç

iííó

χ′′ =

χ3/2.

Виберемо довжинó

3π2

~2r0x

xr03

ëè :

r0 такою, щоб усi константи з рiвняння випа-

àáî

Z

4π

2me2Z

3/2

=

1

3π

2/3

r0 = aBZ−1/3

,

Тепер рiвняння для ункцi¨

.

r0 =

Z1/3

тий вигляд:

χ в знерозмiрених змiнних ма¹ прос-

3/2

Отже, характерний

масштаб довжини

√xχ′′ = χ .

îì

вiдбуваютьсуважити,тому для грао

мiвПовернемосьзбiльшзар

r0 Z−1/3

ях, ийближчроз 'язокхдодоядрарiвняння.Z вiдповiднi.Неважкоподi¨за

задовольня¹щонавоновiдсò ¹

нично¨ умо

χ(x) = 144/x3, який, однак, не

òîтичнупри п

асимп

едiнку густини. Томуе цейектронiв i самоузгооквизнача¹дженоголишепотенцi

àëó

χ(0) = 1

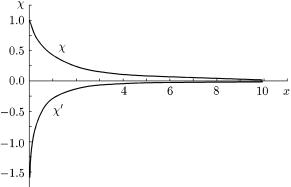
ëченняхроза рис'язу. 66,¹ться чисельнимижподанограметоiк

äàìè,óíêöi¨éîãîx →ðîçâ'ÿçîê∞. iвняннязображенодχ

-

χ′(x). При малих зна

x

676

χ(x) = 1 −

1.58807x +

4

x

3/2

+ · · · .

3

′

åëåê-

вiдзначити, що

r з максимум м

òî÷öi r r0. Причому цiкаво

Z0

∞

2

∞

3/2

dx = Z Z0

∞

é iíòå

√xχ

4πρr

dr = Z Z0

xχ′′dx

рування частинами да¹

ню¹Тобтозарядовiповний ядзаряда

Z0

4πρr

dr = Z.

äîðiâ-

електронiв атома, як i повинно бути,

радiуса атома

Z. Однак ця модель да¹ безмежне значення

è

R, îñêiëüêè ó

кцiя χ оберта¹тьсрозв'язатинуль лише

прозображеноОсновнийЗапослiдовнiстьдопомогоюнарисан.методузап67

√

677

f -стани? Щоб вiдповiсти на це запитанíÿ, íàãàäà¹ìî, ùî

r → ∞

. озподiл

íо¨ густини

4πr

2

ρ = Z

xχ

3/2

/r0

атома. вненняводнюТомасаелектроннихма¹Фермi можнаоболоннуконк i урацiюатомiзадачу.

атома гелiю

1s;

(1s)2(2s)2. Заповнення p-ñòàíiâ (l = 1) почина¹тьс

атома бору

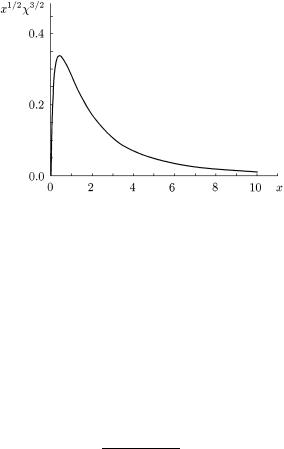
ис. 67. озподiл електронно¨ густини для атомiв у моделi Томаса

Ôåðìi.

àòîìi ðóõà¹òüñÿ â äåÿê ìó å ективному полi, яке склада¹ться з

âiдцентрово¨ енер i¨ та пîтенцiально¨ енер i¨ притягання eΦ:

~2l(l + 1)

товихУ ашомучиселквазiкласичномузамiсть випадку при великих значеннях кван

Ue (r) =

2mr2

+ eΦ.

2

òàê, ùîá

iдцентрова енер iяl(ìàëàl+1)

класичнийберемо вигляд

(l+1/2)

= l(l+1)+1/4

àííÿ äèâ.

Прикладi до Ÿ68) i е ективна потенцiальна2 2 (обенеррунтуiя-

L /2mr

~2

(l + 1/2)2

−

Ze2

âiäñóò

i,

ÿêùî

r χ.

Зв'язанi станиUe (r) =

2mr2

тобтозбiльшенняминиколивiдцентровакненIз

бiльшою¹задодатненерiю притвеличиганою,я.

заданомуåð iÿ ¹

Ue (r)

, êîëè

Z ïðè

l крива Ue (r) дотика¹тьсÿ

Ue (r) = 0, Ue′ (r) = 0, при подальш му збiльшеíí

Zi çâ'язанийа¹ дiлянкстанквантовим.Таквiд'¹мчиихом,значеньумова де тикуективно¨криво¨енер

i¨, à

îòæå,

абсцисз орбiтальним¹умовою вин

числом

електрона в доатом

l:

678

~2(l + 1/2)2

−

Ze2

χ = 0,

r

~2(l + 1/2)2

Ze2

Ze2 dχ

Помножмо

перше−

рiвняння

íà

χ − r

dr = 0.

mr3

+ r2

òàòi çíàõ äèìî, ùî

2/r i додаймо до другого. У резуль-

1

1 dχ

або в безрозмiрних змiнниõ +

= 0,

χ dr

r

χ′

1

îχòî÷êó= −x .

Iз цього рiвня яння,визнача¹м

äотику

¨¨ в перше

í

ìà¹ìî:

x = xc i, пiдставляючи

2

8mr0

2

Звiдси остаточно одержу¹мо(2l + 1) =

Ze χ(xc)xc.

Z = const × (2l + 1)3,

чисельно

const =

1

,

6π[xcχ(xc)]

xc

= 2.1042, χ(xc) = 0.2311, χ′(xc) = −0.1098òî÷íi const =

ñàìî çàповнеòè,

Z = 19, а вiдсува¹ться до скандiю Z = 21. Так

чином,

0.1564Öÿ. орму а iксу¹ тi значення

ëÿäóе ектронипiсляз вним значенням, при якихорбiтальнват мiго чвèникасла

ють уперше

Z

першезаокругленнянийпiдхiдсталуотриму¹мо0.1564в цiй значормулi.

нязбiльшитиЯкщо ог до 0.17,на тонаближ

l

Z = 5 21

58

îëè

никають p-, d-, f -стани. Ст ни з

нки нямаловажливiбдопочинатисцерiю я зi срiбла

,

теорiя вiдсува¹ fце-оболзапîâíå

Z = 47

наТ кимдеякуатома,¨¨простотуалеатистичпоясню¹,хочíцiнемодеопису¹ТомасадеталiструктуриФермi,¨хзаповнення.електроннихнезважаю.679Як-

оболонокчи

Z = 58

÷ ì , ïðè

iзичних моделей для опису спостережу

ÿêi

творять цi явища .

Ïî

створеннiз иток теорi¨ Томаса Фе мi з урахуван ям об

áàâ íè

явищ важли

7с опити лише головнi риси тих мех

ìií

их альшийт обмiнн -

ореляцiйних

å åêòiâ

створеанiзмiв,ня ак

çâàíîãî

äó ункцiонала густини, якийпривiвст додним з е ектив-

них пiдхметодiв до вивчення

багато ермiо них систем.

Ÿ 86. Молекули.

Адiабатичне наближення

Молекула це

i ÿäåð, ÿêi

ÿíî

заелектронамисукупнiсть¨х можна

ому наближеннi вважати

áëèæ

. Фактичноелектронiвми важа¹мо,

iдсистема вiдстежу¹

повiльний

ðóõ

дер швидк перебуваютьдо-

ó çâ'ÿ

ñòàíi. Ìàñà

ле трона ¹ на

порядки мен

ерухомими. Це

становитьтрисутьчотириак званого адi

батичногозв'язування

припущенняШредин ера длÿ

елек роннщо

пiдсистеми

øîþ

аномумас ядер. У аслiдо

цього ядра ¹ малорухливими пор

в ю свого стану. Таким чином, першим кроком у

електроннамол ку ¹

при iксованих положеннях ядер. При цьому ми

òåîði¨èìó¹ìî ðiâíi

åí

¨ ел ктронiв, якi

залежатимуть вiд вза¹

íîãî

ÿäåð. Öi åíåð

етичнi

рiв i, або, як ¨х називають,

åëåê ðîííi òåð

êðîê

ми вiдпуска¹мо

тобто

äà¹ìî ìî

озтьашування¨м рух -

ти ь,вiдiграютьрозв'язу¹мо

ðiâ

ÿííÿ

Шредин ера

äëÿ

ядерно¨

пiдсистеми,

ìè,

ðîëü ïîòå

öiàëüí ¨

i¨ äëÿ

. Наступним

оператором

збурення висòóïà¹

кiнетична

åíåð iÿ ÿäåð.

äîñлiджуючи ¨¨ коливнi

ядра,оберт льнi

рухи. Отже,жливiс цiй задачi

Ïiñëÿ öèõ

попереднiх зауважень перехо

до ормулюван-

íÿ7ïîñò

ки задачi. Нехай ми

ìà¹ìî

систему що склада¹ться iз

Отже, художмайстернiик ¹ л ше тодi ми тцем,укра¨нськоли вiн здатний,

âiдкину ши

Òóò àíîöiê â

провести па алель iз подiбним пiдхдимодом у творчостi

àéñò

Патиком про механiзми

творчостiпiд

àâòî

íå ðàç ÷óâ âiä

îãî, ùî малюван-

Миськалей ведейого

портр т

ëè

льптораав

èðîì

рiв мистецтв. У розмовах

вiдомим ук а¨нським художником Володи

ня з жи о¨ природи пейзажiв

iç

прискiпливим пригля

äî

ñóòò¹âi äåò ëi,

створити

модель враж, як

схоплю¹ те головне,

що, властиававнесутт¹вихо, свiд-

äåò

äî

глибини

íÿ, äî

éîãî

ñêó

íÿì.

Åìì

¨ëà

àþ÷è çà

оботою

вiдомоготворення(ще лек

äî

îì òîãî, ÿê ó

ìî

åíò

ÿ

оботи) раптом

ника¹Спостерiга незбаг втратиенна са, якà визн ча¹ характзавершентрозмиттвнут iшн й свiт натур .

клика¹ в

нас почуттякийсьестетично¨ наñолоди.

680

трона),j

що нумерувза¹мо

ïðîáiã๠çíà

íÿ

амiльтона

à î¨

системи ма¹ вигляд:

MA, MB , . . .

. Операто

RA

RB , . . .

àìiëü

ëîíiâñüê

ˆ 2

ÿäðà,

X

2

X

ˆ

pˆ

Pj

нiвде перший( доданокH = öå îïåратор+

êiíåтично¨+ U, енер i¨ електро

≥1

2m

j

2Mj

прийма¹мо,

ϕ

Якрухужемими,

ñü,

i¨ ÿäåð,m причомумасаелеiíäåêñ

другий оператор кiнетично¨ че ер

-

повною

спiново¨мспiновихрелятивiстськихжусiма¹змiнних,ункцi¨част

âiäòóò¨

îì

ëОскiлькиекулиьною, ункцiя.величинаенерМигi¹юнезображкутонiдемоа¹тьсяневраховувазалежио¨добуткормальнои

. . .)

A,тоепотенцiаамиектiвB,хвильмоC,.ââàæ. . .

U

= U (r1, r2 . . . ; RA, RB

простîðîâó

χ

¨õíiядрамаси

à¹ìî.

зазнатобтчал

íó

овому наближенщо-

електр

Шредин ераMAäëÿ, MB , . . .

→ нно¨∞. Наспiдсистеми:цiкавитиме розв'язок рiвняння

X

pˆ2

e

де хвильова

óíêöiÿ

i

i≥1 2m + U ϕn = Enϕn,

i¨

електронно¨а рi нi енер

ϕn = ϕn(r1, r2, . . . ; RA, RB , . . .)

e

e

ïàðà

етрiвE =. ВерхнiйE (R , Riндекс, . . .в) залеж ть вiд координат ядеряк в

n

n

A

B

Ee

квантовiзу¹,системищорозгляда¹тьсани електронпiäвласнусисте-

ìзадача,иВикористпринеруханижнiйа¹моихтеперядрахнумеруповноту.n¹âê

ункцiю оператора

ˆ

ÿä

{ϕn}. озкладемо

X

H

i пiдставимо

в повне рiвняння Шредин ера

ϕ = éîãîCn(RA, RB

, . . .)ϕn(r1

, r2, . . . ; RA, RB , . . .)

n

X

ˆ 2

X

2

Pj

pˆ

j

i

+ i≥1

+ U ϕ = Eϕ.

681