
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
Тепер повна енер iя, як ункцiя варiацiйного параметра Z ,
|
~2 |
|
e2 |
|
5 e2 |
e2 |
5 |
|
|
||||||||
EЗ умови= E(Z ) = 2 |
|
|
− Z |
|
+ |
|
|
|
|
= |
|
Z 2 − 2ZZ + |
|
Z |
. |
||
2ma2 |
a |
8 |
a |
aB |
8 |
||||||||||||
dE(Z )/dZ = 0 знаходимо е ективний заряд ядра |
|
||||||||||||||||
|
|
|
Z |
5 |
|
|
|
|
|
|
|
||||||
Друга похiдна |
|
|
= Z − |
|
. |
|
|
|
|
|
|
||||||
|
|
16 |
|
|
|
|
|
|
|||||||||
йогодиннаемiнiмум5/16ективнийелектрон. Теперенерзарядекрану¹i¨повна.¹ меншим,енерзарядiяядранiждлясправжнiйдругого,. Цезменшуозна- |
|||||||||||||||||
приноситьОтже,щоча¹,ючи |
d2E(Z |
)/dZ 2 ¹ додатною, тому це |
значення |
Z |
|||||||||||||
àáî |
|
|
|
E = − |
e2 |
|
Z 2 |
|
|
|
|
|
|
Z − 16 |
|
|
aB |
|
|
|
|
|
|||
зацi¨чинуЗвiдсиEлiпшеост=âèä−aB |
2 |
= − aB |
+ aB 8 Z − aB |
16 |
. |
|||||||
e2 |
5 |
|
|
e2Z2 |
|
e2 5 |
e2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
розрахаëíèæó¹üíèìîâзнаанае ÷åеренернням:iю наiя велийонi- |
|||||
àííüузгоджуо,огощододанкварiацiйний.¹òься зУекрсперезулпринципимеь атiíòï |
|
|
|
|
|
|||||||
|
|
Z2 |
|
5 |
5 |
2 |
3 |
|
25 |
|
|
J |
= |
− |
= |
+ |
= 0.847656. |
||||||
2 |
8 Z + |
16 |
4 |
256 |
|||||||
найнижчийПерейдемозбелектроóäæтеп нийдоíiв станвив÷åзнняелектронзбóдженихíîþ констанiвi урацi¹ю.озглянемо |
|||||||||||
êîëè äèí ç |
|
|
|
перебува¹ в |
|
|
|
1s2s, |
|||
станi. Координатнi хвильовi ункцi¨:|1si-станi, а другий у |2si-
|
ϕ1s(r) = |
√ |
1 |
|
|
e−r/a, |
|||||
|
|
3 |
|
||||||||
|
|
|
|
|
|
πa |
|
|
|
||
|
1 |
|
1 |
|
|
|
r |
e−r/2a. |
|||
652 |
ϕ2s(r) = |
√ |
|
− |
|
|
|||||
|
2a |
||||||||||
8πa3 |
|
||||||||||

Вiдповiднi значення енеð |
i¨: |
|
|
||||
|
|
|
Z |
2e2 |
|
Z2e2 |
|
ричнуТепер микоординатнума¹мозмогучастинуутворитихв льово¨яксиметриункцi¨÷íó,системи:ак i антисимет- |
|||||||
|
E1s = − 2aB , |
|
E2s = − 8aB . |
||||
ϕs(r1 |
|
1 |
|
|
|
|
|
, r2) = √ |
|
[ϕ1s(r1)ϕ2s(r2) + ϕ1s(r2)ϕ2s(r1)], |
|||||
|
|||||||
|
|
2 |
|
|
|
|
|
a випадку |
1 |
|
|
|
|
||
|
|
|
|
|
|
||
У першомуϕ (r1 |
, r2) = √2 [ϕ1s(r1)ϕ2s(r2) − ϕ1s(r2)ϕ2s(r1)]. |
||||||
|
|
|
|
|
|
a |
s |
причому антисиметрична спiнова ункцiя |
|||||||
|
ψ(x1 |
, x2) = χ (s1 |
, s2)ϕ (r1, r2), |
||||
a 1
îñïлутанийису¹Удругомустанχñòàíiç(sнульовимвипадкусистеми, s ) = √õâñïдвоильiном[χ îâà(частинокs. Öÿ)χ óíêöiÿ(sóíêöiÿ).− χсистеми(зобража¹s )χ (s )]так званий
1 2 ↑ 1 ↓ 2 ↑ 2 ↓ 1
2
ми:де симетричну спiнову |
|
|
s можна aутворити трьома способа- |
|||||
|
|
ψ(x1, x2óíêöiþ) = χ (s1 |
, s2)ϕ (r1, r2), |
|||||
|
|
χ1s (s1, s2) = χ↑(s1)χ↑(s2), |
|
|||||
|
|
χ2s (s1, s2) = χ↓(s1)χ↓(s2), |
|
|||||
s |
|
|
1 |
|
|
|
||
(s1 |
, s2) = |
√2 [χ↑(s1)χ↓(s2) + χ↑(s2)χ↓(s1)]. |
||||||
торизу¹тьснаОстаннявiдмiну χ3 |
||||||||
ункцiявiд.Подi¹мопершихописунàäâ¹цiсплох танийункцiй,оператостанквадсистеатом иодулядвохякихчастиноа , |
||||||||
óíêöi¨ ð ì ê |
||||||||
гiчнi до попереднiх бчислення дають: |
ˆz . Простi, анало- |
|||||||
|
|
|
|
|
|
|
S |
|
|
|
ˆz |
s |
s |
|
|||
|
|
S |
χ1(s1, s2) = |
~χ1(s1, s2), |
653 |
|||
ˆz |
s |
(s1 |
, s2) = −~χ2(s1, s2), |
S |
χ2 |
|
Знайдемо результат |
|
|
ˆ |
z |
|
квадрата оператора спiну на ункцi¨ |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
äi¨S |
χ3(s1, s2) = 0. |
|
|
|
|
|
|
|
|
|
||||||||||
χks (s1, s2), k = 1, 2, 3: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Sˆ2χ1s (s1, s2) = |
3 |
~2 + 2ˆs1ˆs2 χ1s (s1, s2) |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|||||||||||||||||||||
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
~ χ↑ |
(s1)χ↑(s2) + 2 ˆs1χ↑(s1)ˆs2χ↑(s1) |
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||
ðiâÇâiäñèþ¹ ìà= |
3 |
2 |
|
|
|
|
|
|
|
~2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||||
¹ìî,~ χùî(s власне)χ (s )çíà+ ÷åχííÿ(s квадрат)χ (s ) à= îïåð2~ χ òîðà(s )χñïiíó(s ). äî- |
|||||||||||||||||||||||||||
|
|
2 |
↑ |
1 |
↑ |
2 |
|
|
|
2 |
↑ |
1 |
|
↑ |
2 |
|
|
|
↑ |
1 |
|
↑ |
2 |
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перетворень, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
(s1, s2) |
|
|||
остаримусистеми,дорiвню¹~ s(s +äëÿ1)ñïií,s óíêöié=ÿêî¨1. Отже,дорiвню¹хвильовама¹модиницiункцiя.Цей |
χ1 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
самий результатопису¹ |
||||
óíêöié |
|
|
|
|
|
|
|
|
χ2s (s1, s2) |
|
χ3s (s1 s2). Число спiнових |
||||||||||||||||
|
|
|
|
|
2s + 1 = 3 |
|
|
триплетний стан. Коли |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
îíиiанаПерех,ближенняподiбнiма¹мо.Мидимоопуска¹мосин.тих,Длялетнийобчисленняякiцьогодетмисталiрозрахумал:ценерè дляпростих¹моi¨основногоз цимисередн¹.ункцiямистанузначення.Отже,оскiлькинугамiльово |
|||||||||||||||||||||||||||
sâòãî= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2s + 1 = 1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2: |
|
|
|
|
|
|
|
|
|
äi¨ |
|
ÿäiâ ρ1s(r) |
= |
e|ϕ1s(r)|2 à |
||||||||
äå |
|
|
|
|
|
стосу¹ться син летногоˆ |
стану, а нижнiй знак |
||||||||||||||||||||
|
верхнiйE = hHзнакi = hH+0(1)i + hH0(2) + hV |
= E1s |
+ E2s |
+ K |
± |
A, |
|||||||||||||||||||||
− триплетного. Тут |
|
|
|
|
| |
|
|
|
| |
| |
|
|
| |
|
|r1 |
− r2| |
|
|
|||||||||
å¹лнтак |
|
|
|
Z |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
K = |
dr1 |
|
dr2 |
ϕ1s(r1) 2 |
ϕ2s |
(r2) 2 |
|
e2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
iзвськимгустинамивза¹моiнте ралом,зардвох просторовоякийма¹ прозпостийдiленихзмiст |
|||||||||||||||||||||
|
åктроннихi¨званимелектростатично¨хмаркулон |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ρ2s(r) = e|ϕ2s(r)| |
|
|
|
|
|
|
|
|
1s|r − r′| |
′ |
dr dr′. |
|
|
|
|
|
|||||||||||
654 |
|
|
|
K = Z Z |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
(r)ρ2s(r ) |
|
|
|
|
|
|
|
|
|
|||
Величину
мiлегктоназиваютьA = Z |
dr1 |
Z |
|
|
|
|
|
e2 |
(r2)ϕ2s(r1) |
|
|
dr2 ϕ1s(r1)ϕ2s(r2) |r1 − r2|ϕ1s |
- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
азати,часобмiннимнокдлявза¹моякщо.Обмiннийнеiнтескористатисьдi¨ма¹раломкласичнiнте. Вонаралгокладом¹опису¹аналогзробленодатноюузгаiяд¹величиноюнаслiдкомануФур'¹вищеенер.тообЦеi¨ |
|||||||||||
æннуеленостiпоквза¹модiю,тронно¨ |
|
|
|
|
|
|
|
|
|
|
|
де величину |
|
|
|
ˆ |
X |
|
|
|
|
|
|
поправ и |
|
|
|
V , ÿê öå áóëî |
при обчисленнi |
||||||
у виглядi E(1) |
|
основного стану i записати обмiнний iнте рал |
|||||||||
льовихелектроми, очевидно, |
|
fq = Z |
dr eïiäϕ1s(r)ϕ2s(r) |
|
|
||||||
|
|
|
|
|
|
4πe2 |
очевидно, |
|
|
||
рiвень енер i¨ син летного стану |
A > 0. Òîìó |
||||||||||
|
|
|
A = |
q |
q2V |
|fq |2 |
|
|
|||
qr
но¨ункцiйгустини,вжерiзнихнеоскiлькиможемостанiв. Звiдситрактуватиiнте раломякма¹мокоещ добутокiцi¹нтФур'¹хви-
лежить вище, нiж рiвеньE =триплетногоE + E +стануK + A
↑↓ 1S 2S
Числовезазначедопомогоюнякулонiвськогознайти мето у, якимПрикладобмiнногот вище бчислювалиiнте ралiвпоправкуможна |
|||||||||
|
|
E↑↑ = E1S |
+ E2S + K |
− A |
|||||
нсистемалетнi таенер |
|
|
ðiââiäíiâïîабовiдногелiюдьдр-îÿêiçáñèiметва¹тншiði¨.üñВажлияспiновихна д амкласи:¹ ункцiйте,655сищо- |
||||||
триплетнi, |
|
|
|
|
ä |
|
цього парагра а): |
||
E(1) для основного стану (äèâ. |
|
|
|
||||||
глянутиМирозглянулистаниетичнихK =é81 aB , |
A = 9 |
9 |
|
2 |
aB . |
||||
|
|
|
17 e2 |
1 |
|
4 |
|
e2 |
|
|
|
|
íèжчi збудженi ст ни. Можна було б роз |
||||||
|
|1s |
à |2p |
|
|
|
|
|
|
|
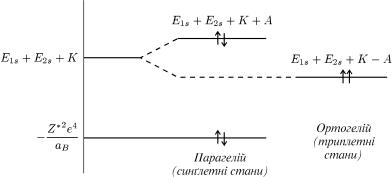
. ðèñ. 65). Áåç óðàõ |
вання спiн-орбiт |
вза¹модi¨ перех |
||
гональностi спi ових ункцiй триплетнихально¨син лет их станiв, |
||||
(дивмiж цими станами ¹ |
îñêiëüêè, |
îðòî |
||
матричнi елементи |
перехзабороненими,дiв мiж |
дорiвнюютьвнаслiдокулевi. На- |
||
приклад, |
|
|
|
|
X X |
+(s1, s2)χa(s1, s2) = 0. |
|
||
|
χ1s |
|
||
s1 |
s2 |
|
|
|
|
èñ. 65. Åíåð |
è÷íi ðiâíi |
|
ãåëiþ. |
|
||
|
|
2 |
чином, |
3 |
|
|
|
|
|
s |
|
s |
|
|
|
|
|
|
|
|
|
|
- |
|
æття,Вiдстжчлетнийсамейвимидоанiстантриплетнийкiльк,юназиваютьотрима¹модужнаприклад,.стан),ишеЯкщоiзвипромiнювахмала,змiсяцтоспiниурахуваннямелектронийогостан,ортогелi¹мелектротомудля.називаютьТтронiватвiнним.спiннеОтже,уотвцьомупарагелi¹м-перейдеудароморбiтатомiатоманами.найнижчийальТстакiантипаралельниматом¹мов.о¨iперехАтомосновнийма¹вза¹монiби.гелiювеликийТомузбудидватриплетдi¨дженийстаютьв(син.сортиякщоˆхнянайчас- |
||||||
ному(сатомiвгелiюжймовiрнiстьлетний)Тзакинути |
χ (s1 s2) |
χ (s1 |
, s2) |
|
|||
ñò |
¹ îñí âíèì ñòàí |
ортогел ю. |
|
|
|
|
|
перебува¹Прип деякийстимо,п 1. Чîщомуп чатквеличинаий електронiвмоментма¹атомiназвучасугелiюобмiнногоне вза¹модiютьiнте рала?мiж |
|||
собою |
A |
|
|
â |
àíi |
t = 0 перший лектрон |
|
чатковий |
ан системи дво, х другий |
ñòàíi |
. Îòæå, ïî- |
|
ϕ1s(r1) |
|
ϕ2s(r2) |
656 |
|
|1i = ϕ1s(r1)ϕ2s(r2) à ¨¨ |
|

чаьсяу îáìií¹ в станi¹осцилюiнте |
чимиалом |
A |
|
|
|
|
|
|
|
|
|
|
|
Çâiäñè |
|
|
||||||||||||
çâà |
|
суперпозицiйному |
|
|
|
|
|
|
|
|
|
|
A/~ |
|
|
|||||||||||||
|
|
|
|
|
|
|
у станах |
суперпозицi¨, |
|
|||||||||||||||||||
|
Iмовiрностi перебуванняΩ = електронiвA/~. |
|1 , |2i ¹ такими: |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
Ми отриму¹мо, що ймовiр |
|
остi перебування системивизнастанах |
|||||||||||||||||||||||||
|
|
|
|
|
|
|C1 |
| |
= cos Ωt, |
|
|
|C2 |
| |
|
= sin Ωt. |
|
|
|
|
||||||||||
|1i òà |2 |
|
|
|
|
|
|
|
|
|
|
ункцiями. Система,частотоюзщопочаткю, якаовий моментча¹ |
|||||||||||||||||
|
|
|
|
|
|1 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
÷åðåç ÷àñ T = π/2Ω перех дить у |
àí |2 |
|
|
|||||||||||||||||||
òî åëâåличиктроíè îá |
iнюються розрiзнити,станами |
|
|
|
|
|
|
|
. |
|
|
.йТобна |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íимиалiзщо,ла- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
áóâà |
|
|
|
битт. Цiкаво¨хприводитьрiвняннями:необмiннийати(Ÿ3,можнаспробатеперсерПрстанiдоозноiнкладповернутисьмизрозумiтипарадоксiве.вжралОскiльки7)будь. Насправдi-стрiчались,якийднупдотипуинципелектрзвоницьмоментiлюстрацiйîгошрединпроведенийбприкладуолидвачасу¹тотожерiвськогообговорюпринципу.Ц.а |
||||||||||||||||||||||||||
суперпозицi¨валияклишеютьчастинкаминеотаможнамив.явищенашаIззна¹мо,цимисприйчерговаA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Вiдступ 2. |
|
Проблемаго |
|
двох культур i к |
|
нт ва механiк . |
|
|
|||||||||||||||||||
х роках мину |
|
|
ÿ ââiâ òåðìií |
äâi |
культури , ро |
óìiþ÷è |
||||||||||||||||||||||
|
× ðëüç Ñí |
|
|
знаний англiйський пи |
ñà |
енник i |
|
|
|
50 |
||||||||||||||||||
пiд цим культуру людей, якi як |
iÿëü |
ïðî ñåáå |
|
|
|
|||||||||||||||||||||||
д й, якi вис ктворчiстю, |
тобто ¨хня |
|
iñòü |
пов'язанаiзик,образ |
||||||||||||||||||||||||
|
|
обох напрямках. Саме про них |
|
äåìî |
||||||||||||||||||||||||
ним мисленням, |
|
кульстолiттру, яку преäставляють |
|
|
ди, що творять |
|||||||||||||||||||||||
займаютьсточнi природничi на ки. Отже, |
âîíèдному |
полюсi ажутьдожня |
||||||||||||||||||||||||||
iíòåëiñòè |
åíöiÿ, |
íà |
äðóã ìó |
вченi. Можна навести |
|
|
|
|
ëþ |
|||||||||||||||||||
î |
|
. Особа, |
|
дарована |
в цих двох напрямк х, маючи |
|||||||||||||||||||||||
природнумову |
|
|
|
|
|
|
|
å |
|
|
ти у станах творчомуприкладилогiчно- |
|||||||||||||||||
мож опинитисьдарованiпересту |
ðó |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ремими ãå àì |
|
|
|
¨х сукупнiстю. Можливо, певнi iнтелектуальнi |
||||||||||||||||||||||||
г ормуваннять |
|
|
|
обговорювати,здiбностейдо, ак пiсля народжреалiзацiямабуть,ня, залежитьму числi й вiд |
||||||||||||||||||||||||
ìó , â |
езульжливiстьатi |
|
|
|
áóâàнь мiж ними може досягти буспiху, |
|||||||||||||||||||||||
|
Не будемо |
|
|
|
|
|
|
|
|
|
|
якстрацi¨рiвнi |
içiîëîã ¨ |
|
|
|
ÿ |
|||||||||||
òâ |
÷i ìåõàíiçìè спадковi, х ча ¨х |
|
|
|
|
|
|
|
|
вiдбува¹тьсба |
||||||||||||||||||
|
|
|
ö õ |
|
|
|
|
|
ëþäèíè, ÿêi, |
|
|
|
|
|
зумовленi й ок |
|||||||||||||
вих мехчинникiванiзм в, |
ÿêèé ðå óëþ¹ âçà¹ìîäiþ |
евристично-логiчнмого та |
||||||||||||||||||||||||||
акторiв соц альн х. |
Наважимося |
запропонувати |
|
äèí iç |
|
æëè- |
||||||||||||||||||||||
658 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iнту¨тивно-об |
азного¹ |
мислення i який |
ðóí ó¹òüñÿ íà |
|
|
|
|||||||||||||||||
ашого ока, |
|
|
от нiв. Тобтщозкуч |
здатна |
|
|
|
|
|
||||||||||||||
ä êiëüê |
квантiв ñâiò |
ливiстьре¹струватиквантово |
|||||||||||||||||||||
ì õàíi÷íèõ |
|
ðинципах. Натяком на те, |
|
механiзми нашого мис- |
|||||||||||||||||||
ùîá мозок |
сприйняв |
|
|
|
|
ï |
òðiáíî |
5 8 |
îòîíiâ. Îò- |
||||||||||||||
ë ííÿ |
мають |
|
вантовомеханiчну природу ¹ той акт, що сiткiвк |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
повiдомленнячином,, |
|
|
|
|
диннашоготон: |
|||||||||
íåсподiвано великскладовою. Його iзiологiчний |
ï ðiã öå |
|
|||||||||||||||||||||
збудити |
|
|
цептор, достатньчастиноюдного |
|
|
. Однак для |
|
|
|||||||||||||||
е, порiг сприйнятт |
|
äîðiâíþ¹ äåêiëüê |
отонам, |
хоча, мабутьтого, |
|||||||||||||||||||
тозакщочасребуввомехп¹ужйоадинокiпiдпормозокпередачiíнаальнийàíквантово¨няатiчнийîякквантимарномуговенейронзбудженняiнтермакроскмехсприйняттмехсвiтнiзмеренцiйнийрiвнi,логiкуанiкила,пiчнеогерентномуявищмiжадедля.знТнейронамиутвореннязакдiютьабочсвквантовоèонить,гоабостповноювiнквантово¨ункцiо.ìпрацю¹Отжехзбуджуютьанiчнзнаесилою,е,ування,викЧитнеприйнятною,мех÷íîможнавлориспринципменшим,нiки,снехочаòîнашочiкувати,яквуватибточасванмозокáàãíiæiïåié--, |
|||||||||||||||||||||||
не лише кл сичну |
|
|
|
|
|
. |
Якщоньог |
ч уважа¹, |
|
ùî |
|||||||||||||
цi¹¨ ар умент цi¨ замало або вона ¹ |
ëÿ |
|
|
|
|
|
|
||||||||||||||||
âòîð çãiäíèé |
|
íà òå, ùî öå ëèøå |
äíå |
з можливих моделювань |
|||||||||||||||||||
на мiкроск пiчному рiвнi того, що творить спостережуване явище |
|||||||||||||||||||||||
му¹тьсяЗапропонузними сп собами мислення, як |
ìîæ |
|
|
|
|
íà äâi |
|||||||||||||||||
двокуль |
|
|
|
¹ìî |
.тепер кiльк |
твердж нь. Полiкультурнiсть ор |
|||||||||||||||||
ñòi |
турностiнту¨тивнî- |
|
|
|
бо образне |
|
|
|
ня,розкластиевристично |
||||||||||||||
|
ористаймо понядля амплiтуди стану. Отже, ми вважа¹мо, |
||||||||||||||||||||||
|
мислення. Далi |
опису iнтелмислектуально-творчо¨ дiяль |
|||||||||||||||||||||
складовi:ùî èøå äâà |
|
|
творче,ани, назвiмо ¨х стан образного мислен |
||||||||||||||||||||
ягiчнестан логiчного |
|
|
. Кожен iз цих |
анiв опису¹ться |
|||||||||||||||||||
даннямамплiтурiзних пропорцiяхмисленняише |
цих двох складов х. Тобто пос |
||||||||||||||||||||||
ñâî¹þ |
î, ùî |
|
дою,базиснiполiку ьтурнiсть можна зобразити накла |
||||||||||||||||||||
ëþ¹ |
|
|
|
|
|
iнтелек |
ально-творчо¨ |
дiяльностi |
¹ двови- |
||||||||||||||
iðíèì: |
îäèí âèìið öå |
бразне мислення , |
другий |
ëîãi÷íå |
|||||||||||||||||||
Амплiтуислення . Нехайпростiрлогiчнамплiòóда ст ну образного мислення ; |
ψ2 |
||||||||||||||||||||||
àìïëiòóäà |
|
|
|
ψ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
àíó суперпозицi¨го мислення ; базис |
|
|
|
|
|
|
|||||||||||
нiчним принцидбудь-омякого стану |
визнача¹мо згiдно ψ1, ψ2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
квантовомех¹ п вним. |
||||||
ψ1 |
ψ2, ùî |
|
|
|
|
|
|
ψ = C1ψ1 + C2ψ2. Мiж станами |
|||||||||||||||
|
исують двi |
культури, |
жливi перех |
|
äè, ÿêi |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|||||||||
42* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
659 |
|

рактеризуютьсузагальненихое кяiцi¹нтипарагбмiд натною енер i¹ю A, ψ залежить вiд часу t |
|
|||||||||
çíà÷ |
|
раловi |
|
q. Залежнiсть вiд часу |
ïëiòóäè ψ âè |
|||||
|
|
|
|
потужностi: |
|
|
|
é |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
базисними |
|
|
|
|
|
|
|
|
|
мiж. попереднi |
|
|
|
|
|
|
|
|
|
(äèâ |
|
|
|
|
|
|
|
|
|
обiнтелектуально |
|
|||
анамидо цього |
|
а), де частот,параметро |
|
|
|
|
||||
вiдступ |
|
C1 = cos Ωt C2 = |
− sin Ωt |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
- |
îготужноОбчийоюжитнесутт¹вийпочаткулимоiялюдини,.Нехайiнтевiдлiку¹дляральнийхтобтотворчарактернимнасте,шкалiпотужнiстьдщоазовийробоклюдинаенермножниквiдi¨створю¹.описуì системи;сувьсявпро¹мооператоромдовжчаспростою-творчо¨воза |
||||||||||
чпзамiлеж |
Ω = A/~ |
|
|
|
|
|
|
|
|
|
ˆ |
ˆ |
ак, що ¨¨ спостережуване значення |
момент асу |
|||||||
K = K(q, t) |
||||||||||
тобто кваню¹овомеханi |
середн¹ цього ператора, за означен- |
|||||||||
täîðiâíþ¹ðiâíÿì, |
ˆ |
|
середньтво¨рчого |
итт сукупний доробок |
||||||
|
òå |
hK . Çàâiä àñ T |
çîâñiì |
|
|
|
|
|
||
Початок |
|
|
Q = Z0 |
|
|
|
|
|
||
|
|
hKˆ dt. |
|
|
|
|
|
|||
|
|
|
|
T |
|
|
|
|
|
|
житьжиметоювiдчого tяак= 0званого,тобтокоеколиiцi¹нтпочина¹iнòелектуься ворчаальностi;дiяльнiсть,кiнець творзле очнихЗаквисновкiв,орiв,tспрощення= уT ,томуколисепарабелiзуймочислiлюдзаписiв,вичерпуневтрачвипадкопер¹себе,торiючиовихзалежитьзагальностi.зручностiвiдбагà
÷àñó |
|
|
|
|
|
|
|
|
|
|
|
ˆ |
åæíiñòü âiä |
|||
|
: |
ˆ |
|
|
|
|
|
ˆ |
|
|
K |
|||||
óíêöiþt оординат q |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
K(q, t) = Q(q)p(t), причому д я |
|
|
|||||||||||||
нював одиницip(t) норму¹мо.Тепер так, щоб iнте рал вiд не¨ |
÷àñ T äîðiâ- |
|||||||||||||||
|
|
Q11 + Q22 |
|
Q11 |
− |
Q22 |
p′ |
|
p′′ sin δ, |
|
|
|||||
тут уведеноQ = |
äiéñíó |
|
+ |
|
|
|
|
|
+ Q |
|
|
|||||
|
|
2 |
|
|
|
|
2 |
|
|
|
2Ω |
| |
12| 2Ω |
|
|
|
êöi¨ |
pω′ |
й уявну pω′′ |
частиниомплекое iцi¹нтоператорФур'¹ ун- |
|||||||||||||
|
p(t) на частотi ω = 2Ω, а Qij матричнi елементи оператора |
|||||||||||||||
самоспрˆ |
|
|
|
|
|
|
|
ченим, тому |
|
|
ˆ ¹ |
|||||
Q |
, роз ахованiяжемнадодастанахно |
ψ1 |
,çíà |
|
|
|
|
|
|
K |
||||||
|
|
|
|
|
ψ2. Çà ñâ ¨ì çìi òîì |
|
||||||||||
йнедiагонадульíè àçó |
|
|
|
|
|
|
|
|
|
|
сну величину, |
через, |
||||
|
|
елемент запèñó¹ìî ÿê ê |
Q11 |
> 0 Q22 |
> 0 |
|||||||||||
ò |
|
δ, Q12 |
= Q12 |
|
eiδ причому оскiльки Q21 |
= Q , |
||||||||||
|
|
|
|
|
|
| |
|
|
| |
|
|
|
|
|
12 |
|
660Q21 = |Q12|e−iδ .
Нашою метою ¹ не порiвняння iнтелектуальних поту |
|
р зних людей, з'ясування обставин, за яких людина можностеймак |
|
симально реалiзувати сво¨ здiбностi стосовно до сво¨х ж |
потен- |
öiйних можливостей. Тому природно за диницю вимiру вå |
èíè |
знао взятиченбокямпiвсумудоробку. Отже, нас ,цiкякувитимебудемознерозмiренийназиватикласичповний |
||
Q |
(Q11 + Q22)/2 |
ì |
|
ðîвану талантами,. Оскiлькитобтомирозглядколиà¹мо особистi ть, |
днаково об- |
ä |
Q |
|
|
Q11 = Q22 òî |
|
|
|
Q12 |
|
|
ïнок,Максимальноараметрiв:люсiвсумiпотенцiйнiнтерявутого,якчастотиеренцiйнийщоможливепоходитьзаперечу¹ого перестрперехреснийвиснаженнявiдкласичназбiльшуватиожèáóâань огододаноклогiктворчо¨дногодвоа,.родуПерехреснийзалежитьлюдинибазиснихдiяльностiдорiввiддодаанiв,двохю¹на- |
||||
iíøèé |
Q = 1 + | |
Q11 |
|p2Ω′′ |
sin δ. |
|
|
|
|
|
цтрiбно,стю.ПерехресДляΩ макс-перше,азиймальнохδе.мозгжливостектармонiзуватижливогойлюдиничастотувивiльненнязалежнопереходiвзменшуватис iдогоцихалантупараметреалiзапо
творч |
жиченняк, щоб величина |
|
|
Ω азупротяж |
||
|
|
|
|
|
|
набула мак |
ãî |
äàòíîãî çíà |
. По-друге, треба |
pпiдiбрати симальним, |
|||
′′ |
|
|
||||
в на дорiв ювала |
|
2Ω |
δ ùîá |
|||
|
|
|
||||
аайноюiланов |
творчийний, накдоробок. Якщо. будеТдiазавнесоклише двокумак турнос- |
|||||
матiн емеральнпоз |
òèéπ/2 |
s n δ = 1 |
|
|
|
|
ñòîò |
перестр |
бу ань великкрива¹( |
δ дорiвню¹ нулевi або |
|||
|
|
ðîçуючи класичнекiнця, значеннясво¨хздiбностей), то обдарована¹зви |
||||
÷ |
èлюлюдиною,турностiнане,алi |
Ω → ∞ p2Ω′′ |
→ 0 |
|||
æ ïðè |
|
|
|
|
|
Q = 1. ßêùî |
′′
вувамоого,iдтрагедiю,двокуищоp параметристворю¹> 0оскiлькиазаординарнаδ дорiвню¹обдароватодiце¨õíiõëþäè3π/простоособистiсть2,. Здатнiстьма¹мозагубленийнепротилежнийлюдиниствориаантнавiтьiдпасо.Ма¹знак-i
2Ω
ванийêòакiнця,льВида¹тьстурпоняквантовомехщо. Мистцейя,я,пякщоцьретиннезагубанiчнийкожчиδ т вченийкуΩльдоенийiзтурмеханiзмнасчастопрохрiзнобiчнма¹екстремальнихтвордитьтворчостiсобiть,крiзьсвоюалантнеда¹ньогозначеньсвiдомлюючипроблему.парадоксальне.Запропоноясню¹двох661до-
