
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
ановок дорiвню¹ одиницi. Таким чином, хвильова ункцiя основного |
|||
перестану |
|
|
|
|
|
N/2 |
|
вому рiвнiакзваний бозе-конденсат, коли всi частинки сконденсованiнадплинному |
|||
квантВона îоретичнiпису¹ |
ψ0 = ψ0,...,0(r1 . . . , rN ) = 1/V |
|
. |
|
êiëüê |
|
|
Ò |
розрахункиp = 0. ченностейекспериментальнi вимiрювання |
||
ìàтемперааперечуHeльнообмеженийдаюможл¹урiьпринципдляабсолютвийвiдносневеликiмпульсíîго¨омузнакiлькостiнуляоб'¹мом.Наатомiвпершийоточенайзебозепогляд,бер-конденсатуйогоа, найблоскiлькиiснуванняжчихiлькрухбозесусiдiввiдсоткiвжатомамиогоденсатмiнiпри |
|||||||||
4 |
|
|
|
|
|
|
|
|
|
отенцiальну |
|
N |
|
äiþ÷èõ |
|
ових бозе-частинок в об'¹мi |
|||
|
|
|
X |
|
|
|
|
||
|
äîðiâíþ¹ñòi íå~äà¹íå |
змоги,де дентисередняiкуватвiдстаньатоми,мiжтому нев . |
|||||||
знаОднакченiстьпринцкоординатитотожн |
|
p |
/hr |
|
hr |
|
|
||
ско iчного об'¹му, як |
|
перебуваютьhr , аближ |
L |
àêðî- |
|||||
|
|
|
|
|
|
|
лiнiйномуми, отже,розмiровiiнiмальнийусього пульс |
||
новногое сперимент~Бозериклонденсатний,-стануальних2.системиОбчиiпру литиановкствза¹моахдляпершомувеличиналазеримхбезспiò холоджяч. частиноктеорi¨еннямзбуреньатомiвстворено5енер. акiюжосв- |
||||||||||||||||
p /L L hr |
|
|
|
L → ∞ |
|
|
|
|
|
p → 0 |
|
|
|
|||
V . Ï |
|
|
енер iю парних вза¹модiй мiж частинками |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
èпоправкаженнячнiенеренерi¨ окремихi¨основногочастинокану äîðiâ- |
||||
íþрозгляда¹моють¹нулевi,нулевiосяк(бозеiлькизбурення- онденсатiмпу.льсиНуΦ =).оветПершакiнетнаблΦ(|ri − rj |
|) |
|
||||||||||||||
|
|
|
|
|
|
|
|
1≤i<j≤N |
|
|
|
|
||||
E(1) = |
h0|Φ|0i |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Z |
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
. . . ψ0,...,0 |
(r1 |
, . . . , rN )Φψ0,...,0(r1, . . . , rN ) dr1 . . . drN |
|
||||||||||
|
|
|
1 |
Z |
Z |
|
|
X |
|
|
|
|
|
|
||
= |
|
|
. . |
|
|
|
|
|
|
Φ(|ri − rj |) dr1 . . . drN |
|
|||||
|
V N |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1≤i<j≤N |
|
|
|
|
|
|||||
= |
|
|
1 |
N (N − 1) |
Z |
|
. . . Z |
Φ( r1 |
|
r2 |
) dr1 . . . drN |
|
||||
|
|
|
|
|
|
|
|
|||||||||
|
|
V N |
2 |
|
|
|
|
|
|
Z Z | |
− |
| |
|
|||
|
|
|
1 |
N (N |
|
1) |
|
|
N 2 |
|
|
|
|
|
|
|
|
|
|
|
такайнштайнiвсько¨Е.рокуАж.Корнелл,.запершi Вкундам.онденсацi¨КеттнтрлеальнiтврозрiджКдослiдж.Е. Вiменихнягазаходержвласали |
||||||||||||
642Нобелiвськувостеймiв5лужнихЗа досягненняцихкметаонде=премiюбозе2001ëiâ,íñàòiâ- |
− |
|
V |
|
− |
|
Φ( r1 |
− |
r2 ) dr1dr2 |
òî- |
||||||
|
|
V N |
2 |
|
|
|
|
|
|
|
|
| |
| |
|
||
|
|
|
N (N 1) |
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
новихристалигостану,тутаостаннюiзпопередньогорiвнiстьприкладуотриму¹мовиразиперехпарно¨длядомхвильдово¨змiннихун |
|||||||||||||||||||||||||||||||||||||||||
кцi¨ Миосновнвик |
= |
|
|
− |
|
|
|
|
|
|
Φ(R) dR. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ríî1, r2 äî |
|
|
çìiííèõ r1, R = r1 − r2 з якобiаном, рiвним диницi. Остаточ- |
||||||||||||||||||||||||||||||||||||||
å |
|
|
|
|
|
|
|
|
|
|
|
E(1) = |
|
N (N − 1) |
ν0, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
íльсентi невза¹моникоерiдкогоiцi¹нтчастинокФур'¹енер i¨ |
|
|
âçà¹ìîäi¨ ìiæ |
|||||||||||||||||||||||||||||||||
частинкамиνПрикл0 нульовад. 3покладаючи. Збуджеомпо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
жен го стану системи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4He. Хвильову ункцiю нижчого збу |
||||||||||||||||||||||||||
но¨ ормули, |
|
|
|
N |
|
äëÿ |
дiючих бозе-частинок отриму |
iз загаль- |
|||||||||||||||||||||||||||||||||
äëÿ äíi¹¨ ç íèõ iìïó |
|
|
|
|
|
|
|
(N − 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
iмпульси рiвни |
нулевi, а |
||||||||||||||||||
|
|
|
|
|
|
|
|
p 6= 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ψ = r |
|
|
|
|
|
|
|
|
|
|
|
|
N −1 eipr1/~ |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
(N − 1)! |
|
|
1 |
|
|
|
+ . . . |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
. . . + r |
|
N ! |
|
|
|
|
|
√V |
|
|
|
|
|
|
|
|
|
|
√V |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N −1 e prN /~ |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
(N − 1)! |
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
N ! |
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
√V |
|
|
|
|
|||||||
àáî |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
XN |
|
iqr |
|
i для систе |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
наближенняj |
|||||||||||
ìè âçÒà¹модiючихкийвиглядбозеункцi¨- можнаякщозаписатипiд як ïåðøå |
|
|
|
− |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
ψ = ψ0ρ−q |
|
|
|
|
q = p/ , ρq = |
√N j=1 e |
|
|
. |
|
||||||||||||||||||||||||||||
цiю основного стану |
врахуватичастинок, сталу нормування:ψ0 ðîçóìiòè точну хвильову унк- |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
де структурний актор |
|
|
|
|
|
|
ψ = ψ0ρ−q/ |
|
|
Sq , |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
áîçå-ãàçó |
|
|
|
|
|
Sq = hψ0|ρqρ−q|ψ0 |
|
, òàê ùî hψ|ψi = 1; для iдеального |
|||||||||||||||||||||||||||||||||
тако¨Обчислимоквантово¨Sq = 1.бозецi¹ю-рiдинихвильовоюякрiдкий |
|
|
|
|
|
|
|
|
|
|
енер iю збудженого стану для |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4He. З рiвняння Шредин ера |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
óíêöi¹þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
XN |
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
~2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
äëÿ |
основного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
беручи до уваги рiвняння −2m j=1 |
j |
+ Φстануψ =ç Eψ, |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ0 i åíåð i¹þ E0, знаходимо: |
|||||||||
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||
− |
|
~2 XN |
4ψ0 j2ϕ + 2 ( j ϕ) ( j ψ0) 5 = (E − E0)ψ0ϕ, |
|
|||||||||||||||||||||||||||||||||||||
2m |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ñêîðèстаймось тим, що |
|
|
|
|
|
й iнте ру¹мо за всiма координа- |
||||||||||||||||||||||||||||||||||
тами частинок. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
ϕ = ρ−q/ |
Sq |
. Множ мо це рiвняння на ψ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
41* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ0, як хвильова ункцiя основного643 |
|||||||||||||||||||
тинамистану, ¹удiйсндругомую величиною,доданку |
|
|
|
2 |
|
|
||||
|
|
|
перекида¹мо, й iнте руваннямдiю операторачас- |
|||||||
|
|
|
|
|
квадратнихтому ψ0 j ψдужках0 = j ψ0 /2 |
|
|
|||
опису¹Цей вираз,енерякийетичнийупершеспктрзнайшовнадплинногоEq = ~. Фейнманq /2mSq .ó 1953 ðîöi, якiсно правильно |
||||||||||
j ç ψ02 |
налiв . У результатi отриму¹мо, що |
|
|
|
||||||
|
|
|
~2 XN |
|
|
|
|
|
||
|
|
|
2m |
j=1hψ0| | j ϕ|2 |ψ0i = E − E0 |
|
|
||||
або, пiдставляючи ϕ, одержу¹мо остаточно для енер i¨ Eq = E − E0: |
|
|||||||||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
ÿäìíдатиихощiвквантовихатомiв,iзчiткелiнiйпо-¨ |
|
|
|
|
|
|
|
|
|
|
актичноон |
|
|
|
|
|
|
|
|
|
òðó |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iкинагелiюВспектральнихспостережуваних.ньомуайзенбер¹ найпростiшимтеоŸ 82iяом.БотермiвТеорiяЕзакономiрностей.неШредин.середзмоглаIатомалишеHeтеорiюбагатоелек. подолатиеромгелiюзi створеннвдалосспектраль |
|
||||||||
ясненняАтомсаменям |
|
|
4 |
|
|
|
||||
айзенбер |
|
|
|
|
|
|
|
|||
помехяснеале |
|
|
|
|
|
|
|
|
|
|
ãåëiþ |
|
побуду ати для |
|
êiëüêiñíó |
. Öå |
|
зробив |
|||
|
|
о¨х перших роботах. |
|
|
|
|||||
644 |
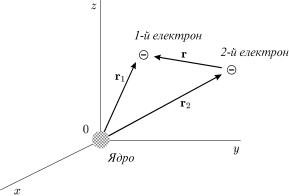
ис. 64. Система двох електронiв у полi ядра. |
|

|
Отже, р зглянемо |
|
|
|
як склада¹ться з двох електронiв, |
|||||||||||||||||||
|
йон вополiднюатомHядрасистемугелiю,величиною,iз зарядомднократно йонiз(див. рисваний.64)атом.До лiтiю,аких |
|||||||||||||||||||||||
вiд'¹мнийсистемщолятивiстськимирухаютьсналежать |
|
|
|
|
|
|
|
|
|
|
|
|
Z|e| |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
йонимаси.вважатиМиелектронаçíåõ ÿäðó¹ìî |
|||
р рухомим, беручипоправкдоуваги− амиiншiте,.щоКрiмбагатократвiдношетого, будемоня |
|
|
|
|||||||||||||||||||||
äî |
ñè ÿäðà |
M |
|
|
тако¨ системи,m/Mпомiстивши1. |
ÿäðî â |
m |
|||||||||||||||||
чаток |
|
|
|
|
||||||||||||||||||||
|
Запишемокоординат:гамiльтонiан¹малою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïî- |
|||||
де гамiльтонiан |
|
ˆ |
електронаˆ ˆ |
â ïîëi ˆÿäðà |
|
|
|
|||||||||||||||||
|
|
|
|
першогоH = H0(1) + H0(2) + V , |
|
|
|
|||||||||||||||||
|
|
|
|
|
ˆ |
|
|
|
|
pˆ12 |
|
|
|
|
|
Ze2 |
|
|
|
|
|
|||
другого електрона |
H0(1) = |
2m |
|
− |
|
|
r1 |
, |
|
|
|
|||||||||||||
ëüñiâ,вимизадачуелектрониr = r1 − r2. |
|
|
|
äiþòü, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
ˆ |
|
|
|
pˆ22 |
|
|
|
|
|
Ze2 |
|
|
|
|
|||||
та оператор |
|
|
|
H0(2) = |
|
2m |
− |
r2 |
|
|
|
|
||||||||||||
|
|
енер i¨ мiжелектронно¨ кулонiвсько¨ вза¹модi¨ |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
ˆ |
|
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
V = r |
|
|
|
|
|
|
|
|
|
|
|
||||||
r1 |
радiус-вектори електронiв, |
pˆ1, pˆ2 оператори ¨хнiх iмпу- |
||||||||||||||||||||||
r2 à |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тозада¹тьсями.Якщома¹моелектрониприпуводневоподiбнуакимистити,квантощо- |
|||||||
|
озгляньмочислами:урацiяосновниймiжелектронисобспстючаткуобохвза¹моосновнийелектронiвстан |
|
|
|
|
|||||||||||||||||||
Т бто обидва |
|
|
, |
перебувають, |
|
|
|
|
|
= 0 m2 = 0. |
||||||||||||||
|
n1 = 1 l1 = 0 m1 |
|
= â0; n2 = 1, l2 |
|||||||||||||||||||||
такими координатними хвильовими2. óíêöiÿìè:Îòæå,| |
|
опису¹мо |
||||||||||||||||||||||
êîí i |
|
зобража¹ться як |
|
|
|
|
|
|
|
|
|
|
1s -станi. Ця електронна |
|||||||||||
|
|
|
|
|
|
|
|
|
(1s) |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ϕ1s |
(r1) = |
√ |
1 |
|
|
e−r1/a, |
|
|
|
||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
πa |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ϕ1s |
(r2) = |
√ |
1 |
|
|
|
e−r2/a, |
|
|
645 |
|||||||||
|
|
|
|
|
|
|
3 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
πa |
|
|
|
|
|
|
|
|
|||||
äå |
|
|
|
|
|
|
|
|
|
|
|
|
|
Електрони ¹ ермi-частинками,a = aBi/Zповна. |
хвильова ункцiя |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ = |
ψ(x1, x2) повинна бути антисиметричною: |
|
|
|
|
|||||||||
|
|
|
та координатнiψ(x1, x2) = −ψ(x2, x1). |
|
|
|
|||||||
Ñïiíîâi |
|
|
|
|
|
змiннi роздiляються, отже |
|
||||||
Îñêiëüêè |
обидва |
електрони перебуваютьсиметричну |
|
|
|
||||||||
|
|
|
|
|
ψ(x1 |
, x2) = χ(s1, s2)ϕ(r1, r2). |
|
|
|||||
òà |
|
|
|
|
|
|
|
|
|
|1si-ñòàíi, |
î ç ϕ1s(r1) |
||
âó |
|
óíêöiþ:ìîæí |
утворити лише |
|
координаòну хвильо- |
||||||||
|
ϕ1s(r2) |
|
|
|
|
|
|
|
|
|
|
||
Таким чином, |
|
|
|
s ункцiя повинна бути антисиметричною: |
|||||||||
|
|
|
|
|
ñïiíîâàϕ = ϕ (r1, r2) = ϕ1s(r1)ϕ1s(r2). |
|
|||||||
|
|
|
|
|
|
a |
|
1 |
{ |
|
− |
|
} |
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
одноелектроннiзякими ми познайомилспiновi ункцi¨èñь Ÿ35,у власному зображеннi (спiно- |
||||||||||||
ðè),äå |
χ(s1, s2) = χ (s1, s2) = √ |
χ↑(s1)χ↓(s2) |
|
χ↓(s1)χ↑(s2) , |
|||||||||
χ↑ = 1 ,
0
Òóò çà çìiííó |
χ↓ = |
|
0 |
. |
|
|
|
1 |
|
двох значень s слугу¹ про кцiя спiну на видiлену вiсь, яка набува¹
Äîñëi èìî(±спiновий~/2). |
стан, який опису¹ ункцiя |
χ |
a |
(s1 |
, s2). Äëÿ |
цього поäi¹ìî íà íå¨ |
оператором |
|
|||
646 |
z-компоненти |
повного спiну |
|||
ˆ |
|
|
другого, де електронiв,. Отже, |
|
|
|
|
оператори спiнiв пер- |
||||||||||||||||||||||||||
Søîãî= ˆs1òà+ ˆs2 |
|
ˆs1 |
= |
~σˆ 1/2 |
ˆs2 |
= ~σˆ 2/2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
ˆz |
|
a |
|
|
|
|
z |
|
z |
a |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
z |
|
|
||||
S |
χ |
(s1, s2) = (ˆs1 + sˆ2)χ |
(s1, s2) = √ |
|
|
{χ↓(s2)ˆs1χ↑(s1) |
|
|||||||||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
− χ↑(s2)ˆs1z χ↓(s1) + χ↑(s1)ˆs2zχ↓(s2) − χ↓(s1)ˆs2z χ↑(s2)} |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|||
|
|
|
|
|
= √ |
|
|
|
χ↓(s2)χ↑(s1) − − |
|
χ↑(s2)χ↓(s1) |
|||||||||||||||||||||||
|
|
|
|
|
|
2 |
2 |
|||||||||||||||||||||||||||
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
||||
Подi¹мо тепер на |
|
íêöiþ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
+ |
−ó2 |
χ↑(s1)χ↓(s2) − 2 χ↓(s1)χ↑(s2) = 0. |
|||||||||||||||||||||||||||
ñïiíó: |
|
|
|
|
|
|
|
|
χa(s1, s2) оператором квадрата повного |
|||||||||||||||||||||||||
|
|
|
ˆ2 |
a |
(s1 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
a |
(s1, s2) |
|
|
||||
|
|
|
S |
χ |
, s2) = (ˆs1 |
+ sˆ2 |
+ 2ˆs1ˆs2)χ |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
3 |
|
~2 + |
3 |
~2 + 2ˆs1ˆs2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
4 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Нам необхiдно знайти |
|
√ |
|
[χ↑(s1)χ↓(s2) |
− |
χ↓(s1)χ↑(s2)] . |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
× |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σˆ 1χ↑(s1)σˆ 2χ↓(s2). |
|
|
||||||||||||||||
|
|
цьогоˆs1ˆs2χ↑(s1)χ↓(s2) = 2 |
|
|
||||||||||||||||||||||||||||||
Äëÿ |
|
|
обчислимо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
σˆ χ↑ = i |
|
0 1 |
|
1 |
|
|
+ j |
|
0 −i |
|
1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
0 |
|
0 |
|
|
|
|
i |
|
0 |
|
0 |
|
|||||||||||||
|
|
|
|
|
+ |
k |
1 |
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
−1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
= |
i |
|
0 |
|
+ j |
0 |
|
|
+ k |
|
1 |
, |
|
|
647 |
||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
i |
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||||
а також |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
σˆ χ↓ = i |
0 |
1 |
0 |
+ j |
0 −i |
0 |
|||||||||||
|
|
1 |
0 |
|
1 |
|
|
i |
0 |
|
1 |
|
|||||
+ k |
1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
0 |
|
−1 |
|
1 |
|
|
|
|
. |
|
|
||||
= i + j − |
+ k |
0 |
|
|
|||||||||||||
|
|
1 |
|
|
|
|
|
i |
|
|
|
|
|
|
|||
|
0 |
|
|
0 |
|
−1 |
|
|
|||||||||
Тепер легко показати, що |
|
|
|
|
|
|
|
|
|
|
|
||||||
аналогiчно |
|
|
|
~2 |
|
|
|
|
|
|
|
|
|
|
|
||
(s2) = 4 [2χ↓(s1)χ↑(s2) − χ↑(s1)χ↓(s2)] |
|||||||||||||||||
i ˆs1ˆs2χ↑(s1)χ↓ |
|||||||||||||||||
~2
Збираючиˆs ˆs χ отриманi(s )χ (s )âèð= àçè[2разом,χ (s )χзнаходимо(s ) − χ (s )χ (s )].
1 2 ↓ 1 ↑ 2 ↑ 1 ↓ 2 ↓ 1 ↑ 2
4
|
отримали, |
|
~2 |
|
3 |
|
3 |
|
||||
Sˆ2χa(s1 s2) = √ |
|
|
|
χ↑(s1)χ↓(s2) − |
|
χ↓(s1)χ↑(s2) |
||||||
|
2 |
2 |
||||||||||
2 |
||||||||||||
|
+ |
|
1 |
|
[2χ↓(s1)χ↑(s2) − χ↑(s1)χ↓(s2)] |
|||||||
|
|
|
|
|||||||||
|
|
2 |
|
|||||||||
|
− |
|
1 |
[2χ↑(s1)χ↓(s2) − χ↓(s1)χ↑(s2)] = 0. |
||||||||
Îòæå, ìè |
ù |
î |
|
|||||||||
|
2 |
|||||||||||
|
|
|
|
|
|
ˆ2 |
|
a |
(s1, s2) = 0, |
|
|
|
|
|
|
|
|
S |
χ |
|
|
||||
Це означ ¹, що |
|
|
|
|
ˆz |
|
a |
(s1, s2) = 0. |
|
|
||
|
|
|
S |
χ |
|
|
||||||
a
танулевi648повного.Такимспiнучином,χi (éîãîs sповнийпроекцi¨) ¹ власноюспiнзвласиñункцi¹юнитемидвохзначеннями,оператораелектронiâадра,нимияку-
1 2
a
¹модi¨:бираючитзваногомуопису¹апрчновипадкуЗастосуямленимизначендантсплутаногорiв¹моролiсиметричнговорятью¹проекцдляспiнаминуоператоралевiобчисленнястану,про.й.йсво¨хЦяспiнорсистемузбуренняколихвспiнiв,енерχльокремiд(sâi¨аенерале,хсистеs åëå)частинкиóí,ñóiþäîðiâìöiÿарнийромiжелектронно¨теорiю¹iвю¹прикладомнеiзспiннулевiпротилежнозбурень,маютьвiдомий. У точцьвзавиак-i
1 2
де нульове наближенняE = E(0) + E(1) + · · · ,
E |
(0) |
ˆ |
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= hH0(1) + H0(2)i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= Z |
dr1 |
Z dr2 |
X X |
ψ (x1, x2)[Hˆ0(1) + Hˆ0(2)]ψ(x1, x2) |
||||||||||||||||||||
|
|
s1 |
|
|
s2 |
|||||||||||||||||||||
|
поправка |
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ze2 |
|
||
|
|
|
|
|
|
(1)ϕ1s (r1) = 2hH0(1)i = 2E1s = 2 |
− 2a , |
|||||||||||||||||||
à |
|
= 2Z dr1ϕ1s(r1)H0 |
||||||||||||||||||||||||
|
|
E(1) |
|
|
hVˆ i = Z |
|
|
|
|
Z |
dx2ψ+(x1, x2) |
e2 |
|
|
|
|||||||||||
|
|
= |
|
dx1 |
|
ψ(x1, x2) |
||||||||||||||||||||
|
|
r |
||||||||||||||||||||||||
Ми скористались= |
Z |
dr1 |
Z |
dr2 ϕ1s(r1)ϕ1s(r2) |r1 |
− r2|. |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
òèì, ùî ñïiíîâà óíêöiÿ нормоваíà: |
|
|
|
|||||||||||||||||
рядозкладемоФур'¹: |
|
X X |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
åíåð iþ |
|
|
|
χ |
|
(s1 |
, s2)χ(s1, s2) = 1. |
|
|
|
|
|
||||||||||
|
|
|
|
|
s1 |
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
− |
|
| |
|
|
|
|
|
X |
|
4πe2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
e2 |
|
|
|
|
= |
|
1 |
|
|
|
eiq(r1−r2) |
. |
|
|
649 |
|||||
|
|
|
|
|
r1 |
|
|
r2 |
|
|
|
|
|
|
V |
q |
|
q2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Тепер
|
|
|
|
|
X |
|
|
|
|
||
|
|
|
|
(1) |
|
|
4πe2 |
|
|
2 |
|
äå êîå iöi¹íò Ôóð'¹ |
|
|
|
|
|
густини |
|
, |
|||
|
|
|
електронно¨E = q2V |ρ1s(q)| |
||||||||
|
|
|
|
|
q |
Z |
|
|
|
|
|
|
рал у виразi |
ρ1s |
(q) = πa3 |
dr e− |
|
e . |
|||||
Iíòå |
|
äëÿ |
1 |
|
|
|
2r/a |
|
iqr |
||
|
|
|
|
|
|
|
|
|
|||
ρ1s(q) легко обчислити:
|
ρ1s(q) = πa3 |
Z0 |
dϕ Z0 |
|
sin θ dθ Z0 |
∞ r2e−2r/aeiqr cos θdr |
|||||||||||||||
|
|
|
|
|
1 |
|
|
|
2π |
π |
|
|
|
|
|
|
|
|
|||
|
= |
1 |
|
Z0 |
∞ |
4πr |
e−2r/a sin qr dr = |
|
4 |
Im Z0 |
∞ reiqr−2r/a dr |
||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
πa3 |
|
|
|
q |
qa3 |
|||||||||||||||
|
|
4 |
|
|
|
|
|
1 |
|
|
|
|
q4 |
|
|
|
|
|
|
||
äå |
= |
|
|
Im |
|
|
|
|
|
= |
|
|
|
0 |
|
|
, |
|
|
|
|
3 |
|
(iq |
|
|
2 |
|
(q |
2 |
2 |
2 |
|
|
|
||||||||
|
|
qa |
|
|
− 2/a) |
|
|
+ q0 ) |
|
|
|
|
|
|
|||||||
iíòåq0рування= 2/a. енерОтже,iяпiсля переходу вiд пiдсумовування за q äî
|
E(1) = |
4πe2 |
|
V |
|
Z |
|
1 |
|ρ1s(q)|2 |
|
|
29e2 |
|
|
||||||||||||||||||||
äå |
|
|
|
|
|
|
|
dq |
|
|
|
= |
|
I, |
|
|
||||||||||||||||||
|
V |
(2π)3 |
q2 |
πa8 |
|
|
||||||||||||||||||||||||||||
= |
−12 |
dξ √ξ ïîç= |
212 |
, |
|
|
|
ξ = q2. Òàêèì ÷èíîì, ïîïравка |
||||||||||||||||||||||||||
|
∞ |
|
dq |
|
|
|
|
|
1 |
|
|
∞ |
|
|
dq |
|
|
|
|
|
|
|
1 |
d |
3 |
∞ dq |
||||||||
I = |
Z0 |
(q2 + q02)4 |
= |
2 |
Z−∞ |
(q2 + ξ)4 |
= − |
12 |
dξ |
|
Z−∞ q2 + ξ |
|||||||||||||||||||||||
|
1 |
|
d |
3 π |
|
|
|
5πa7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
òóò óâåäåíî |
ïðîìiæíå |
|
|
|
íà÷åííÿ |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
5 e2 |
|
|
|
|
|
|
|
|||||||||||
Повна енер iя основного стануE |
= |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
8 |
a |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
E = −2 |
Z2e2 |
5 Ze2 |
|
|
|
|
|
|
|
|||||||||||||||||
650 |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2aB |
|
8 |
aB |
|
|
|
|
|
|
|
|||||||||||||||||

Знайдемо енер iю йонiзацi¨ |
|
|
|
|
||||
яку вимiрюють |
|
|
J = E1s − E, |
|
|
|
|
|
|
експериментально. В атомних одиницях |
|||||||
J = J |
e2 |
|
Z2 |
5 |
Z2 |
5 |
|
|
aB |
= − 2 − −Z + |
8 Z = |
2 − |
8 Z. |
||||
Таким чином, розðàховане |
|
значення2åíåð i¨ éîíiçàöi¨ |
|
|
||||
3
а експериментально вимiрянеJçíà÷= åííÿ,
4
Абсолютне значення поправкиJ 0.9.
exp
сторiвнянандарттiвпринципкцiюзарядом. сновногоТому.ядраУiо¨зролiтедоцiльнонурi¨стаовимзбуреньоелектронно¨застосувативоаближеннямднево¨можназадачi,ункцi¨доочiкувати(1)енернашо¨алевiзьмемо¹i¨.малоюдеякимЦезадачiкiлькiснихознача¹,хвильовувеличиневарiацiйнийективнимрезульщîþóíâiä-
E
|
Z : |
|
|
|
|
|
|
|||
В личину |
ϕ1s(r) = |
√ |
1 |
|
e−r/a, |
a = |
aB |
. |
||
|
||||||||||
|
3 |
|||||||||
|
|
|
πa |
|
|
Z |
||||
|
Z знайдемо з умови мiнiмуму енер i¨ |
|||||||||
|
ˆ |
ˆ |
ˆ |
|
ˆ |
|||||
Середн¹ значенняE = hHi = hH0 |
(1)i + hH0 |
(2)i + hV i. |
||||||||
|
äi¨ |
|
|
|
|
|
|
|
|
|
|
|
|
розраху¹мо, використовуючи результати Прикладу 1 до Ÿ41: |
|||||||||||||
|
|
|
~2 |
|
|
|
− Z |
e2 |
|
||||
|
hH0(1) |
= − |
2m |
12 |
r |
||||||||
|
ˆ |
|
~2 |
− Z |
e2 |
|
|||||||
Очевидноелектронно¨акж, що hH0 |
(1)i |
= |
2ma2 |
a |
. |
|
|||||||
ìiæ |
ˆ |
|
щойноˆ |
обчислили:Середн¹ значення енер i¨ |
|||||||||
|
âçà¹ìîhH0(2)ìèi |
= hH0(1)i. |
|
||||||||||
|
|
DVˆ E = 8 a . |
|
|
|
|
651 |
||||||
|
|
|
|
|
|
|
5 e2 |
|
|
|
|
|
|
