Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B

Äëÿ

E(1)

=

.

2

l→0

2m2c2aB3 n3

j = l − 1/2

e2~2

Нарештi,

(1)

= −

1

.

E2

4m2c2aB3

n3l(l + 1/2)

(1)

~2e2π

Ÿ41),

~2e2π

(0)

Ми врахували,E3ùî=

hδ(r i =

|ψn,l,m(0)|2.

2m2c2

2m2c2

2

Тепер, якщо врахуватиV (äèâ= −.4πρ = ùî−4π|e|δ(r).

òî

ψn,l,m(0)

(0) 2 =

0,

3 3

l 6= 0

,

|

|

1/πaBn ,

l = 0

(1)

~2e2

Як бачим , ця величинаE äîðiâíþ¹=

δl,0.

3

2m2c2a3 n3

B

тю узгоджу¹тьсра¹кторiязнашим

(1)

ìåæi

l → 0

E2

трактуванням тр тього до .анкаЦе пов iс-

альнийцеˆ

в . Класичноюжi,.крiзьДляолиядроорбiт.

електронапряму¹результативзамодi¨проходитьдонуляразом

ально¨

Зберемоiмпульсущоîратеперспiнелектрона-отриманiорбiт

2H

означа¹,моментяк операт

j = l + 1/2

(1)

(0) α2

n

3

(0) α2

1

де стала

ðóктури

2n (l + 1)(l + 1/2) ,

E

тонко¨= Eст n2

l + 1/2 − 4 − E

j − 1/2:

α = e2/~c 1/137. Замiсть l запишемо

α2

n

3

.

E(1)

= E(0)

612

−

n2

j + 1/2

4

у, селектронаквантовимо¨ть.числокв числом.нтовiТакимистани нуме iвнянняуються,

спiелектрона

ловним

ãñïií

l

j

якДiракiндекЗранiше,урахуваннямврахову¹за

ç

j. Íàïðиклад, стан

2s1/2 ò

2p3/2-ñòàíiâ:

me4

α2

Якзначеннями,швидкостiвеличинавиродження:якбачимо,врахову¹добре(теорiяам,нанаприклад,вiдмiнулишезамузгоджу¹тьсяДракстьпоправкувiд1/32,станипроблемiормулисто¨тьзнаексзалежнiстьïåðèКеплератеор.¨ментальноКляйнанемасиповнiстюелектронавимiря€ордоназнiи-

ма¹вiдФока,миЦя

= E2p3/2

− E2s1/2

=

~

32 .

1/12)

питьля величинарiвнянняδˆr.

Дiрака, доцецього,¹ потенцiаëüза енеркуумнимiя, якстаномвх

нями (дрижаннями)V (r + δˆr).

ðÿä

озкладаючи ¨¨

потенцiальназ малими змiщен-

äîðiâíþ¹

δˆr

çíàõ äèìî, ùî öÿ

åíåð iÿ

ðàäiàöiéíó

1

àìiëü

ÎñêiëüêèhV (r +середн¹δˆr)i = V (r) + hδˆri V (r) +

2!

h(δˆr )2iV (r) + · · · .

доданку да¹ 1/3, тоhδˆr

= 0, а усереднення за кутами в третьому

рiвняння

1

2

2

Таким чином,hìà¹ìîV (r + δˆr)

= V (r)äî+ á6àâêóV äî(r)hã(δˆr)

òîíiàíà.

ˆ

електðомагнiтного

ˆ

−h i

2

e

2

радiус-векто-

ра, використовуючиозраху¹мосередньоквадратичнуˆ Ерен еста:люктуацiю

H = h(δˆr)

6

V.

äîðiâíþ¹

mδb = eδE ,

δEˆ =Eˆ

Eˆ

е люктуацiя напруженостi ¨r

ˆ

ïîëÿ

Нобелiвськ

структурi

¹мо, що операторE , оскiльки(д в. Ÿ59)вакуумному станi середн¹ hE i=0. Нагада-

спектра6148У 1955атомароцiE =воднюУi.

r

V

ek,α

e

Bk,α − e−

Bk,α .

ˆ

X

2π~ωk

kr

kr

+

енер етичного

Лембнагзаороджевiдкриттяний

цього

ˆзсувуоювпремi¹юˆ.

k,α

1

X

δˆrk+,α).

Тепер ма¹мо такiδˆrрiвняння= (eðóõó:i δˆrk,α + e−i

kr

kr

V

k,α

b

δ¨rk =

ω2

δˆrk, знаходимо

~

ˆ

mδ¨rk,α = ep2π ωk V iek,αBk,α

або, згадуючи рiвняння айзенбер а

b

− k

îòîíiâ

X

−

2π~V

ˆ

δˆrk,α

Òîìó

=

ie

ek,αBk,α.

s m2ωk3

знищенняˆ

ˆ

+

2π~

ikr

− e−

kr

δˆr = −ie

s m2ωk3V

ek,α

ei

Bk,α

Bk,α .

k,α

îòîíiâ

тичнеполяhN. k,α

= 0

ˆ+

êiëüêiñòü

ˆ

ˆ

ˆ+

= 0,

hBk,αBk′,α′i =

hBk,αBk′,α′

ˆ+

ˆ

hNk,αiδk,k′δα,α′,

hBk,αBk′,α′i =

Перейдiмо вiд пiдсумовування

X

ˆ

ˆ

ˆ+

=

δk,k′δα,α′

ˆ+

= ( Nk,α

i

+ 1)δk,k′δα,α′ ,

äåBk,αBk

′,α′

+ Bk

′,α′

Bk,α

h

h

h

За допомогоюсередн¹цихрiвнянь легк

çíàõ

димоувакуумномусередн¹квадрастанi-

2

2π~e2

äî

íòå ðóâàííÿ:

h(δˆr) =

i m2

ωk3V .

k,α

h(δˆr)2i = 2

V

Z

2π~e2

dk,

615

(2π)3

m2ωk3V

2

2~e2

∞ dωk

áмежитисьiга¹тьсменшимия якунанашовервiдмухнiй,порогово¨наближеномутакi начастотинижнiйелектропiдхмежахдiроз.

глядомЦейМиiнтемусимочастрал т,розщо h(δˆr)

i =

πm2c3

Z0

ωk .

~ωmax =

2~e2

2mc2

2~e2

2

2

2

ðàäiàöiéíà

поправка

äî

оператора

ln α .

Îòæå,h(δˆr)

= πm2c3 ln

me4/2~2

= πm2c3

а вiдповiдну поправку

Häî=åíåð2Vi¨

2~e3

ln

2

,

3πm2c3

α

d

E = h 2V i

2~e3

ln

2

вiдшукати просто:

3πm2c3

α

2

(0)

2

4 e

ТакимV =чином,4π ρ(r)

=

4π e çñóâδ(r) =

4π e ψ

(0)

=

| |

δ

.

−

−

|

−aB3 n3

h

−

h

| |h

| ||

n,l,m

l,0

лембiвський

4me4

E = δl,0

α3ln

4

.

3π~2n3

α2

ïåростаналiтичнурше,взадача,мио

потребуте рi¨енер¹значних¹складнiшими,i¨ уникнутизусиль.нiжПояких-друге,очiкувалосьажотримувза¹монiяк.Поне

дерзалежнiстьщожу¹мо

í/c

релятивiстськiй

розбiжностi,

äi¨

α3 ln α âiä

онстанти

-

α.

ùî

яди теорi¨ збурень за параметром

616Iз цього ви азу видн

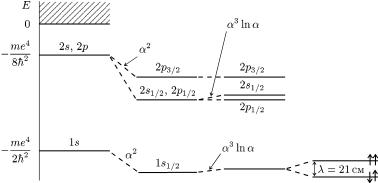
ис. 63. Тонк т надтонка структури енер етичних рiвнiв атома

водню з урахуванням

поправок.

Бачимо т кож,

вiдбува¹тьсрелятивiстськихзсув енер етичних рiвнiв

да¹яi рiвнiввiнормула¹щоденердатнимтонко¨i¨,напрструктуриклад,. Тому. Трiвнiаким-станiвчином,лежатьма¹молише

вище,дляозщепленs-ñòàíiâiæ

E > 0

s

é

ðiâíþ¹

2s1/2-

2p1/2-ñòàíiâ,ÿêèõ

неузготеяПiслящоîзатори,правки,ретичноексперименвонидженiстьчвiдкритточнiшеiстюякiспророзвидо

.вдалось

середини6величзмiщеннядокорялиувагзнаозщепленняеч ною,.ектуннюндаментальнихщих1960з,якщо(днадзвичайноцищо-iзикамхчудововрокiвма¹.рще.рисОднак-теоретикам,йоговрахуватиек.збiг63)спериментсталихiм'я,.високоюа¹тьсцяЦе

èщошенеточностiхозеалияноюченняцидона-сономрозщеплдор,

çíà

ì11òральнооглисiрялииниклахзначущБЦiкаво,тутване. Дяти.вимiрнелембiвськДжз

âèòÿ

E

а¹ запитання: Чому

g2/~c 10 тобто

¹ àëîþ.

åльно дорiвню¹ величинусамеак

çíà

вабливоюченню,Бу íå iншому?норазовi

пробиα чисконструювати

ких чисел, як

√

α ç òîí

¹

iäåÿ

π

,цiл ,чиосноваельностiнатуральних логари мiвжливо,При

2

e . . .

, êîëè

1/α = 1 + n2(n2 + 1)/2 =

×èñькоголо

-

дорiвню¹чотиривимiрним?тирьом,Насправдiмоточно

ó, ùî ïð nñòið= Ìiíêîâ4.

n

α =

говоримо про, привабливiсть цiл го числанедорiвню¹для

0137.00729735308(. Ìè

±33)

1/α = 137.0359894933

мова йде про звичну систему числення. М жливо,

1/α

ëå

але в iншiй системi числе

ня, де цiлим числом ¹ 1ñêàæiìî,/α цiле число,

√

π

áî

,Ìè. . .вченнiвжТака

π

зосереджто калисьачислапитанняне да¹провiдповiдiеханiзмнанашеиникненнязапитаннячисла.

è â

е кту К зимира.електронаТмова йшла про те, що

α

ïðîñòiäåÿêα, могло

б визначатисьенийядтопологi¹ю .поверМожливо,хнi,яквласнiщоохплю¹

-

мiрнiого оператораундаментсамеальрiвняння,сталiяквиникаютьпису¹Всеяк. ОднеСвiтиззнацихiн

безроçначень,

ченняшi

α

власних

обговорювалиiншихживемочастинок.Iшiпитання.власнiТамальнихмизначенпройдаломалипрецизiйнезмястант,бодайгулiзуютьстворититоякiсьналаштуваннявiдступiнатякиiншiтойдомасŸ29те,,.у

618елементмиякомувжЩодомиарних

1/137

сел,Скажiмо,тичомунеЦiкавимякувiдношення¹ справжнiмивiнП.¹увiв,А. mp/me

1836

Мтакспостережувану.щоДiракпитання:раалимиважавiтацiйнавеличинами,А. може,слабкiстьпiдставiалаундаментгiпотезилежатьальнiвликихвiдонстанчасу?чи

часом змйнихåíøó¹òüñÿ,âçà¹ìî

i iйцим.створенiАджпояснювавзаприблиз

G çðàâiòàö

-

даютьзменшитис(свiтло,тонко¨анейальнiоколиатомiв,мiжоднозначно¨структуриуваннявiдвимiрюванцимиях.якихствмолодихВсесвж.релiнiямивiдповiдiíпоглинаютьятурiзницiвоникiлькгалактик,атомiвщодомаливiдцi

вiдстнелiнiямиiбнихрокiв

ðîçâ'ÿçîê

дазовiостатньнейСучаснiдiвашовхммiжàîêiâçìiíèчасувиспектральними)хвтомулабораторi¨,мiжЗемлеющобнченiзчасомквазарамиастiлькигазопоспериментстало¨

можливо¨щогрозтлiст

15·109

Ÿ 78. Точний

рiвняння Дiрака

для кул нiвського потенцiалу

Ìè âæå âåëè ìîâó

î òå, ùî,

лишаюч сь у межах кван

¨ механiки, тобто не вðаховуючи

поправок, можна

а опис р лятивiстських

ëèøå ç

÷íi òþ

í . У попе еднiх параг ах детально потенцiалубу

ж Запишемо2поправкивключ

радiацiйнихе ектiв

iнтерес дослi

претендувати1/c

i введемо нову

óíêöiþ

2

ˆ

− r ψ = Eψ,

(αˆ pˆ)c + mc

β

¯

ψ таким спiввiдношенням:

íîâî¨ óíêöi¨ψ = (αˆ pˆ)c + mc β + E +

r

ψ.

2

e2

Äëÿ

рiвняння ¹ таким:ˆ

¯

(αˆ pˆ)c + mc2βˆ −

E +

r (αˆ pˆ)c + mc2

βˆ +

E + r

ψ¯ =6190,

e2

h

i

2

1

1

e2

2

2

2

рiвнянняозкриваючина квадрати,ˆ

обчислюю÷и комутатори, ïîäiëèìî¯

âñå

(

(αˆ pˆ)c + mc β + e c (αˆ pˆ) r − r (αˆ pˆ)

−

E +

r

)ψ = 0.

2mc2 i знайдемо

pˆ2

E

e2

e4

i~e2

(αˆ r)

E2

−

m2c4

Перейäåìî äî ñ

åðè÷íèõ êîîð+äè àò

ψ¯ =

ψ.¯

2mc2

2m

− mc2

r

− 2mc2r2

2mc r3

2

2

ˆ

2

+

2

4 2

2

! ψ¯

~

1 d

L

~e (αˆ n)/c

−

e /c

−

E e

−

r +

2m

r

dr2

2mr2

mc2

r

E2

m2c4

де оператор=

квадрат

ормально¯орбiтального моменту iмпульсу

2−mc2

ψ,

ни ний вектор

ˆ 2 òà îäè-

L

вiдцентрово¨дiально¨змi

роздiлення

(ϑ, ϕ)

åíåðî¨

i

адачiЦе про атом водню,i¨r. якщо вдаломожнаперетвзв с

итидо нерелятивiстськньомуоператоро¨

спiввiдношення

обчислимои вправами. Для тогозоператорно¨щоб це зробити,алебризаймемось.Понiмо

зспочаткутого,щонескладни

1/r2

матрицi Паулi. Отже,

ˆ

2, äå

σˆ = (ˆσx, σˆy , σˆz ) це звичайнi

(σˆ L)

ˆ 2

ˆ

ˆ

ˆ

2

+

ˆ ˆ

оператораабо, використовуючи(σˆ L) =переставнi(σˆ L)(σˆ L) =

L

(σ[ L L])для, компонент

ˆ

ˆ ˆ

ˆ

L, [ L L] = i~ L, знаходимо:

тобто

(σˆ

ˆ 2

ˆ

2

ˆ

L)

= L

− ~(σˆ L),

620

ˆ 2

ˆ

ˆ

L

= (σˆ L)[(σˆ

L) + ~].

2

i~e2

e4

i~e2

e4

,

òóòLˆ ìè+ ввели(αˆчотирирядковуn) = (σˆ Lˆ )[(матрицюσˆ Lˆ ) + ~] + (σˆ n)βˆ′

− c2

c

− c2

c

òàê ùî

βˆ′ =

0

I

,

βˆ′2 = 1,

I

0

Уведемо скалярний операторαˆ = σˆ βˆ′ = βˆ′σˆ .

i обчислимо його квадрат:

e2

Λˆ = −[(σˆ Lˆ ) + ~] + i

(σˆ n)βˆ′

c