1-1 Основы теории цепей / Лекция № 3-4

Метод непосредственного использования законов Кирхгофа

Расчет сложной электрической цепи обычно заключается в определении токов в ветвях цепи при заданных сопротивлениях всех элементов цепи и известных э. д. с. или задающих токов источников энергии. Общее число неизвестных не может превышать числа ветвей цепи.

Для решения системы, содержащей n неизвестных, должно быть составлено n независимых уравнений, т. е. таких, среди которых ни одно из уравнений не может быть получено с помощью линейных операций над другими.

ХНУРЭ. Профессор кафедры ТКС Шостко И.С.

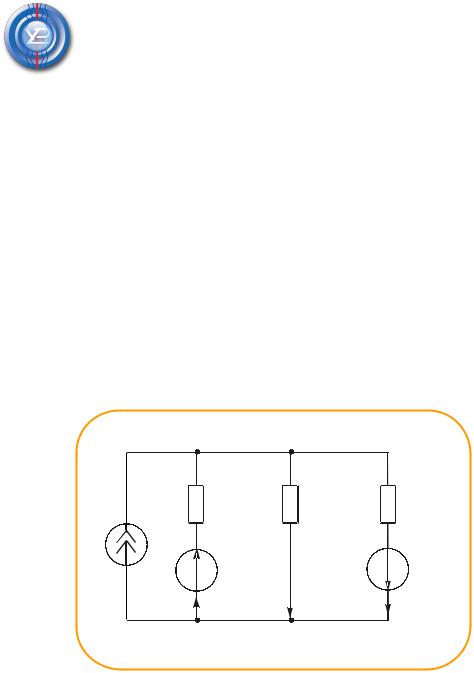
Метод непосредственного использования законов Кирхгофа

Предварительно нужно выявить в схеме узлы и ветви.

Число уравнений должно быть минимальным, но достаточным и равным числу неизвестных токов, т.е.m - mJ , где m – общее число ветвей в схеме; mJ – число ветвей с источниками тока.

По первому закону Кирхгофа составляют n-1 уравнение, где n – число узлов схемы.

Недостающие уравнения дописывают по второму закону Кирхгофа.

ХНУРЭ. Профессор кафедры ТКС Шостко И.С.

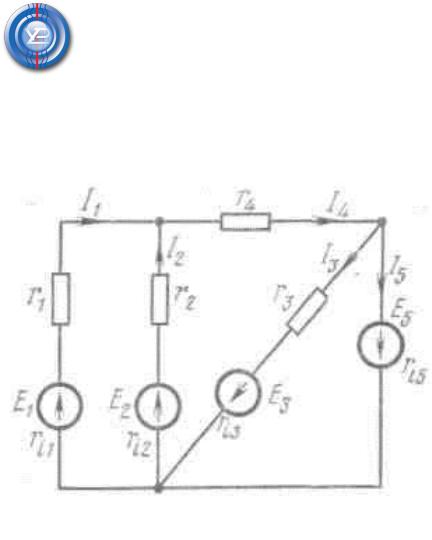
Метод непосредственного использования законов Кирхгофа

Напишем уравнения Кирхгофа для расчета цепи, изображенной на рис. (на рисунке указаны положительные направления токов и э. д. с). Цепь содержит пять ветвей. Поэтому в цепи пять токов. Узлов всего три. Таким образом, по первому закону следует составить два уравнения и по второму

— три. В качестве контуров выбираем ячейки. Уравнения пишем для всех ячеек, начиная с левой и кончая правой. Направления обхода контуров выбираем совпадающими с направлением движения часовой стрелки.

ХНУРЭ. Профессор кафедры ТКС Шостко И.С.

Метод непосредственного использования законов Кирхгофа

Уравнения для двух верхних узлов имеют вид:

I 4 - I 2 - I1 0 I 3 I 5 - I 4 0

Отметим, что, сложив эти уравнения, получим уравнение для

нижнего узла:

I1 I 2 - I3 - I5 0

Сумма всех трех уравнений образует тождество (0 = 0).

ХНУРЭ. Профессор кафедры ТКС Шостко И.С.

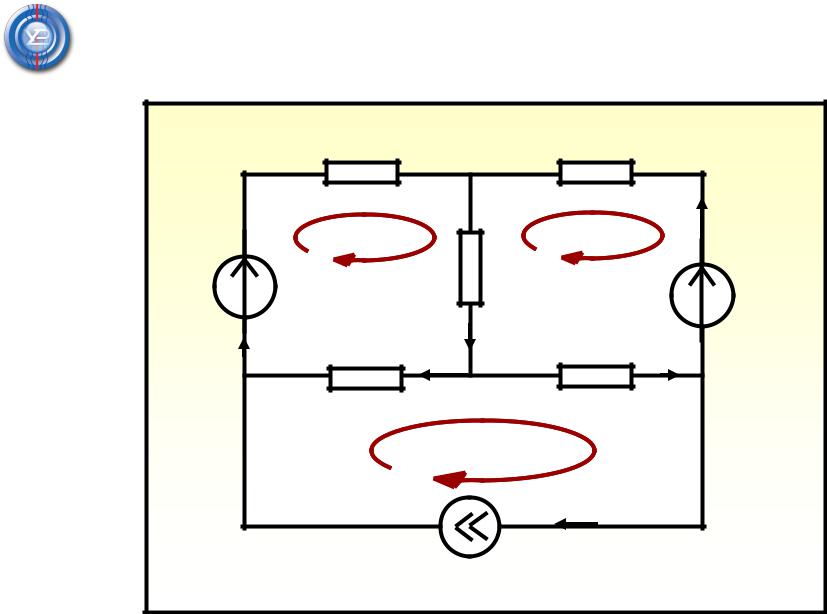
Метод непосредственного использования законов Кирхгофа

J

UJ

ХНУРЭ. Профессор кафедры ТКС Шостко И.С.

nу 4 nв 6

n1 nу -1 3

n2 nв - n1 3

ХНУРЭ. Профессор кафедры ТКС Шостко И.С.

a : I1 - I4 - J 0

b : - I3 I4 I5 0 c : I2 - I5 J 0

ХНУРЭ. Профессор кафедры ТКС Шостко И.С.

1к : R1I1 R3I3 R4 I4 E1 2к : - R2 I2 - R3I3 - R5I5 -E2 3к : - R4 I4 R5I5 -U J 0

ХНУРЭ. Профессор кафедры ТКС Шостко И.С.

ХНУРЭ. Профессор кафедры ТКС Шостко И.С.