ВычМатЭкз

Метод простой итерации.

Описание метода.

Предположим, что требуется найти решение x=(x1 , x2 ,... , xm )T системы с заданной точностью ε > 0. Преобразуем систему к эквивалентному виду:

x1=ϕ1 ( x1 , x2 , ... , xm ),

x2=ϕ2 (x1 , x2 ,... , xm ), (1)

x(2k+1)=ϕ2 (x(1k) , x(2k ) , ... , x(mk)),

….............................................

x(3k+1)=ϕ3 (x(1k) , x(2k ) , ... , x(mk)),

Сходимость метода.

Теорема. Пусть в некоторой σ-окрестности решения х функции ϕt ( x)(t=1,2 , ... ,m) дифференцируемы и выполнено неравенство

Тогда независимо от выбора начального приближения x(0 ) из указанной σ-окрестности корня итерационная последовательность не выходит из этой окрестности, метод сходится со скоростью геометрической прогрессии и справедлива оценка погрешности

x(n)− x ≤qn x(0)− x

Замечание. В ряде случаев при наличии достаточно хорошего начального приближения x(0 ) можно, считая, что q ≈ q0= ϕ' ( x(0)) , использовать практический критерий

окончания итерационного процесса:

x(n)− x(n−1) <ϵ1= 1−q0 ϵ

q0

Метода Ньютона

Этот метод в отличие от метода хорд на k -ой итерации вместо построения хорды требует построить касательную к кривой y F(x) при х хк , при этом за следующее приближение хк 1 принимается точка пересечения этой касательной с осью Ох. Пользуясь этим методом не обязательно знать отрезока,b , где содержится корень уравнения F(x) 0, а достаточно лишь найти некоторое начальное приближение к корню х х0 .

Запишем уравнение касательной к кривой y F(x) в точке М0 (х0 ,F(x0 )) y F(x0) F (x0)(x x0 )

здесь к 0,1,2,..., и F (xk ) 0.

Вычисления по формуле (3.3) надо вести до тех пор, пока не будет выполняться условие

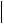xk 1 xk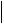

Решение СЛАУ методом Гаусса

Пусть исходная система выглядит следующим образом

Матрица 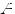называется основной матрицей системы, 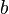— столбцом свободных членов.

Смысл метода Гаусса заключается в том, чтобы преобразовать исходную систему уравнений и получить равносильную разрешенную или равносильную несовместную систему.

Итак, метод Гаусса состоит из следующих шагов: прямой ход:

1.Рассмотрим первое уравнение. Выберем первый ненулевой коэффициент и разделим все уравнение на него. Получим уравнение, в которое некоторая переменная xi входит с коэффициентом 1; 2.Вычтем это уравнение из всех остальных, умножая его на такие числа, чтобы коэффициенты при переменной xi в остальных уравнениях обнулились. Получим систему, разрешенную относительно переменной xi, и равносильную исходной;

3.Если возникают тривиальные уравнения (редко, но бывает; например, 0 = 0), вычеркиваем их из системы. В результате уравнений становится на одно меньше;

4.Повторяем предыдущие шаги не более n раз, где n — число уравнений в системе. Каждый раз выбираем для «обработки» новую переменную. Если возникают противоречивые уравнения (например, 0 = 8), система несовместна.

Обратный ход:

берём значения переменных, полученные из предыдущих уравнений и подставляем их в обрабатываемое сейчас. В итоге остаётся одна неизвестная которая легко находится.

Определение. Две системы линейных уравнений называются равносильными, если множество всех их решений совпадает.

Определение. Элементарные преобразования системы уравнений — это:

1.Вычеркивание из системы тривиальных уравнений, т.е. таких, у которых все коэффициенты равны нулю; 2.Умножение любого уравнения на число, отличное от нуля;

3.Прибавление к любому i-му уравнению любого j-то уравнения, умноженного на любое число. Определение. Переменная xi называется свободной, если эта переменная не является разрешенной, а вся система уравнений — является разрешенной.

Метод Гаусса с выбором главного элемента

суть метода та же, что и у обычного метода Гаусса (смотри вопрос 7), но может случиться так, что на главной диагонали, после ряда преобразований, будет стоять ноль. Эта модификация метода устойчива к подобным ситуациям.

Итак, под главным элементом теперь понимается максимальный по модулю элемент текущей строки в прямом проходе Гаусса. Под прямым проходом я подразумеваю «обнуление» нижней треугольной матрицы. Соответственно под обратным, «обнуление» верхней матрицы.

Фактически, при любом из обходов мы движемся по главной диагонали (хотя, можно и по обратной, смотря кому как удобно), в зависимости от обхода мы это делаем слева направо (прямой), справа налево (обратный).

Алгоритм прямого прохода:

1.Выбрать максимальный элемент строки стоящий справа от текущего диагонального элемента, запомнить столбец, в котором он стоит;

2.Если максимальный элемент равен нулю, то СЛАУ не имеет решения, т.к. в системе присутствую линейно зависимые уравнения;

3.Поменять столбец найденный в пункте 1, со столбцом, в котором располагается текущий диагональный элемент;

4.Разделить все элементы строки на текущий диагональный элемент (он изменился, т.к. столбцы были переставлены);

5.Вычитаем текущую строку из ниже лежащих строк матрицы, умножая ее на коэффициент при соответствующем неизвестном.

Прямой проход завершен, результат – нижняя (находящаяся под главной диагональю) треугольная матрица заполнена нулями.

При обратном проходе вычитаем текущую строку из всех вышестоящих предварительно умножив ее на коэффициент при соответствующем неизвестном.

Стоит заметить, что можно по аналогии выбирать главный элемент не в строке но в столбце.