ВычМатЭкз
.pdf
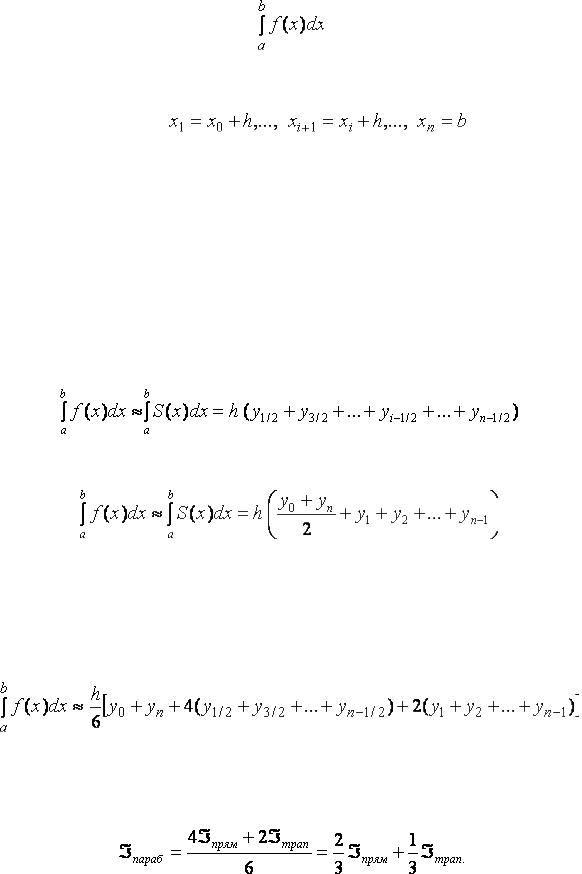
Численное интегрирование. Квадратурные формулы прямоугольников, трапеций и Симпсона
Для приближённого вычисления определенного интеграла
разобьём отрезок интегрирования 
на 
равных частей точками
,
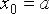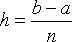− шаг разбиения.
Значения функции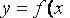 
в точках разбиения 
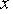обозначим через 
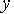. Непрерывная подынтегральная функция 
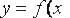заменяется поточечной функцией 
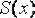, аппроксимирующей данную функцию.
Интегрируя функцию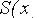 
на отрезке 
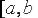, получим некоторую формулу численного интегрирования (квадратурную формулу).
В зависимости от функции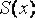 
, аппроксимирующей подынтегральную функцию, будем получать различные квадратурные формулы.
квадратурная формула прямоугольников:
квадратурная формула трапеций:
Можно получить квадратурную формулу Симпсона, называемую также формулой парабол, если сплайн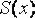 
, аппроксимирующий подынтегральную функцию 
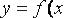, представляет собой непрерывную
функцию, составленную из примыкающих парабол. Потребуем, чтобы на отрезке 
парабола проходила через точки 
, 
, 
.
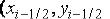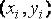после всяких преобразованияй получаем квадратурную формулу парабол (формулу Симпсона):
Приближённое значение интеграла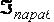 
, вычисленное по квадратурной формуле парабол, можно
выразить через значения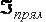 
и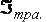 
− результаты вычислений по квадратурным формулам прямоугольников и трапеций:
Погрешность каждой квадратурной формулы оценивается величиной остаточного члена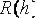 
, зависящего от шага разбиения 
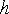(или от числа разбиений 
):
.
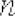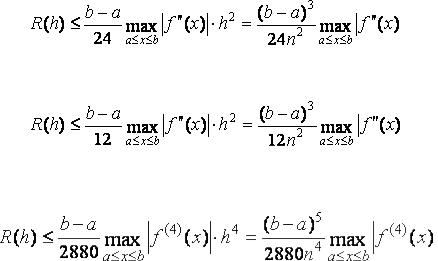
Приведём оценки погрешностей квадратурных формул в том случае, когда подынтегральная функция имеет непрерывную производную второго порядка:
· для формулы прямоугольников
;
· для формулы трапеций
.
Если подынтегральная функция имеет непрерывную производную четвёртого порядка, то справедлива такая оценка погрешности формулы Симпсона:
Заметим, что при интегрировании степенной функции, степень которой не выше трёх, квадратурная формула Симпсона даёт точный результат.
Оценка погрешности методов численного интегрирования. Оценка погрешности по правилу Рунге.
Теорема: пусть функция f дважды непрерывно дифференцируема на отрезке [a, b]. Тогда для составных квадратурных формул прямоугольников и трапеций справедливы оценки погрешности:
I −I h |
≤ |
|
M 2 (b−a ) |
|
h2 , |
|
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
пр |
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
I −I h |
|
≤ |
M 2 (b−a) |
h2 , |
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
тр |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вывод формулы (1). Представим погрешность |
R= I−I прh |
формулы прямоугольников в виде |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R=∫ f ( x)dx−h ∑ f i −1 =∑ ∫ ( f ( x)− f ( xi− |
1 |
))dx используя формулу Тейлора |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
2 |
|
i=1 xi−1 |
|
|
|
|
|
|
|
f |
' ' (ξ) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
f (x )= f (x |
|
1 )+ f ' (x |
|
1 )(x− x |
|
1 )+ |
|
( x−x |
1 )2 |
где |
x [ xi −1 , xi ], ξ=ξ( x) [ xi−1 , xi ] |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
i− |
|
|
|
|
|
|
i− |
2 |
|
|
|
|
i − |
|
|
|
|
|
|
|
|
|
|
|
|
|
i− |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
имеем |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
xi |
|
( f (x )− f (x |
1 ))dx= |
1 |
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
dx , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Ri=∫ |
|
|
|
∫ f ' ' (ξ(x))(x− x |
1 ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
xi−1 |
|
|
|
|
|
|
|
|
|
|
i− |
2 |
|
|
|
|
2 xi−1 |
|
|
|
|
|
|
|
|
t− |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
M 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
M 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ri ≤ |
|
∫ |
(x−x |
1 )2 dx= |
|
( x−x |
1 )3 xi= |
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
2 |
|
xi−1 |
|
|
|
i− |
2 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
i− |
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
M 2 |
|
|
|
M 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Так как |
|
R=∑ Ri , то |
|
R ≤∑ |
( |
|
)h3= |
h3 n |
. Замечая, что nh = b – a, приходим к |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
формуле (1). |
i =1 |
|
|
|
|
|
|
|
|
i=1 |
24 |
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Для вывода оценки (2) воспользуемся тем, что отрезок, соединяющий точки |
N i−1 и |
|
N i |
||||||||||||||||||||||||||||||||||||||||||||||||||
представляет собой график интерполяционного многочлена первой степени |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
y=P1 (x )= f i−1 |
x1−x |
+ f 1 |
x−xi−1 |
Поэтому для формулы трапеций верно равенство |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
xi |
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
h |
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ri=∫ f ( x)dx− h ( f i−1 + f i )=∫( f ( x)− P1 ( x))dx |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
xi−1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
xi−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Используя оценку погрешности линейной интерполяции, имеем |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
R ≤ |
|
M 2 |
(x− x |
)(x |
− x)dx= |
M 2 |
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
t |
∫ |
2 |
|
|
|
|
i −1 |
|
|
|
i |
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 2 |
|
|
|
M 2 (b−a) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
3 |
|
|
2 |
||||
Следовательно, для |
|
R= I−I |
|
|
справедлива оценка |
|
R ≤ |
h |
n= |
h |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ i |
12 |
|
|
|
12 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
||
Теорема: пусть функция f имеет на отрезке [a, b] непрерывную производную четвертого порядка. Тогда для формулы Симпсона справедлива оценка погрешности
I −I h ≤ M 4(b−a) h4
C 2880
h
Правило Рунге оценки погрешности. h I 2 − Ih
I −I 2 ≈ 2k −1
Численное дифференцирование.
Вычисление первой производной.
Предположим, что в окрестности точки x функция f дифференцируема достаточное число
раз. Исходя из определения производной f ' ( x)= lim |
f (x +Δ x)− f ( x) |
естественно |
|
(Δ x ) |
|||
(Δ x)→0 |
|
попытаться использовать для ее вычисления две формулы:
f ' ( x)≈ |
f (x +h)− f ( x) |
|
(1) |
|
|
|
h |
|
|
||||
|
|
|
|
|||
f ' ( x)≈ |
f (x)− f (x−h) |
(2) |
|
|
||
h |
x=h и |
x =−h |
||||
|
|
|||||
соответствующие выбору фиксированных значений |
||||||
Здесь h > 0 – малый параметр (шаг). Разностные отношения в правых частях формул (1) и (2) называют правой и левой разностными производными. + Для оценки погрешностей
f (x +h)− f ( x) h
f ( x)− f ( x−h)
h
формул численного дифференцирования воспользуемся формулами Тейлора:
f (x±h)= f (x )± f ' ( x)h+ |
f ' ' (ξ(±)) |
h2 |
(3), ξ+ и ξ− – некоторые точки, расположенные в |
|
|||
2 |
|
|
|
интервалах (x, x + h) и (x, x – h) соответственно. Подставляя разложения (3) в выражения для r±
получаем |
r+ ( x , h)= |
−1 |
f ' ' (ξ+ )h , r−( x , h)= |
1 |
f ' ' (ξ−)h |
. Следовательно |
|||||||
2 |
|||||||||||||
|
( x , h)≤ 1 M |
|
|
|
|
|
|
2 |
|
|
|||
r |
2 |
h |
|
M |
2 |
= max f ' ' (ξ) |
(4) |
|
|
||||
|
+ |
2 |
|
|
|
[ x , x+ h] |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
− |
1 |
M |
2 |
h |
M |
2 |
= max f ' ' (ξ) |
(5) |
r ( x , h)≤ |
|
|
||||||
|
2 |
|
|
|
|
|
[ x−h , x] |
|
Таким образом, формулы (1) и (2) имеют первый порядок точности по h. Иначе говоря, правая и левая разностные производные аппроксимируют производную f'(x) с первым порядком точности. Приведенные формулы численного дифференцирования имеют геометрическую интерпретацию.
Пусть |
N 0 , |
N− и |
N + |
– расположенные на графике функции |
y= f (x ) |
точки с |
|||||||||||||
координатами |
(x , f ( x)) |
, |
(x−h , f ( x−h)) и |
(x +h , f (x +h)) |
. Вспомним, что производная |
||||||||||||||
f ' ( x) равна тангенсу угла α наклона к оси Ох касательной, проведенной к графику функции в |
|||||||||||||||||||
точке |
N 0 . Формула (1) соответствует приближенной замене производной f ' ( x)=tgα правой |
||||||||||||||||||
разностной производной |
|
f ( x+h)− f ( x) |
, равной тангенсу угла |
α+ |
наклонна к графику |
||||||||||||||
|
|
|
|
h |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
N 0 и |
N + |
|
|
|
|
|
|
|||
функции секущей. Проведенной через точки |
. Формула (2) соответствует аналогичной |
||||||||||||||||||
замене левой разностной производной |
|
f ( x)− f ( x−h) |
, равной тангенсу угла |
α− секущей, |
|||||||||||||||
|
|
||||||||||||||||||
проведенной через точки |
|
N 0 |
и |
N− . |
h |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
Лучшим по сравнению |
tg α+ |
и |
tg α− |
приближением к |
f ' ( x)=tgα |
является тангенс угла |
|||||||||||||
наклона α0 |
секущей к графику, проведенной через точки |
N− |
и |
N + |
. Соответствующая |
||||||||||||||
приближенная формула имеет вид |
f ' ( x)≈ |
f (x +h)− f (x−h) |
– центральная разностная |
||||||||||||||||
|
2h |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
производная.
Подставляя в выражение для погрешности |
|
r0 (x , h)= f ' ( x)− |
f (x +h)− f (x−h) |
|
||||||||||||||||||
2h |
||||||||||||||||||||||
соответствующие разложения по формуле Тейлора |
|
|
|
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||
f (x±h)= f ' ( x)± f ' ( x)h+ |
f ' ' (x ) |
h |
2 |
± |
|
f ' ' ' (ξ± ) |
h |
3 |
, |
|
|
|||||||||||
2 |
|
|
6 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
получим |
r0 (x , h)=− |
f ' ' ' (ξ+ )+ f |
' ' ' (ξ−) |
h2 . Следовательно, справедлива оценка погрешности |
||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
M 3 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
r |
(x , h)≤ |
h2 |
, |
M |
|
= |
|
max |
f ' ' ' (ξ) . |
|
|
|
|
|
||||||||
6 |
|
|
|
|
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
3 |
|
[ x−h , x+ h] |
|
|
|
|
|
|
|
|
|
|
||||
Явный метод Эйлера.
Рассмотрим дифференциальное уравнение
(1)
с начальным условием
Подставив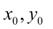 
в уравнение (1), получим значение производной в точке 
:
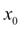При малом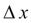 
имеет место:
Обозначив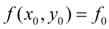 
, перепишем последнее равенство в виде:
(2)
Принимая теперь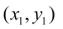 
за новую исходную точку, точно также получим:
В общем случае будем иметь:
|
|
(3) |
|
|
Это и есть метод Эйлера. Величина |
называется шагом интегрирования. Пользуясь этим |
|||
методом, мы получаем приближенные значения у , так как производная |
на самом деле не |
|||
остается постоянной на промежутке длиной |
. Поэтому мы получаем ошибку в |
|||
определении значения функции у , тем большую, чем больше |
. Метод Эйлера является |
|||
простейшим методом численного интегрирования дифференциальных уравнений и систем. Его недостатки – малая точность и систематическое накопление ошибок. Более точным является модифицированный метод Эйлера или метод Эйлера с пересчетом (ну или неявный метод Эйлера). Его суть в том, что сначала по формуле (3) находят так называемое «грубое приближение»:
а затем пересчетом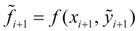 
получают тоже приближенное, но более точное значение: