одного конечного элемента будет всегда прямолинейным независимо от вида нагрузки на балку. В этом заключается один из главных недостатков МКЭ.

Чтобы преодолеть этот недостаток и построить более точную эпюру М, обычно уменьшают размеры одного конечного элемента,одновременно увеличивая общее число элементов в конструкции.

47

4.ПРИМЕРЫ РАСЧЕТА БАЛОК

4.1.Общая схема алгоритма расчета МКЭ

Представим алгоритм МКЭ в форме метода перемещений основными блоками.

1.Задание исходной информации, которая должна включать:

-количество элементов и узлов;

-координаты узловых точек конструкции в общей системе координат;

-взаимное расположение конечных элементов и узлов в местной

иобщей системе координат;

-внешние узловые, поверхностные и объемныеИсилы;

-условия опирания конструкции (граничные условия);

-геометрические и жесткостные параметры каждого элемента конструкции. Д

2.Построение матрицы жесткости конечного элемента в местной системе координат. А

3.Формирование матрицы преобразования координат для перехода от местной системы координатбк общей.

4.Определение матрицы жесткости общей конструкции в общей системе координат. и

5.Приведение поверхностных и объемных внешних сил, действующих на элементС, к стат чески эквивалентным узловым силам (формирование локального вектора узловых сил).

6.Определение суммарных узловых сил в каждом узле всей конструкции (формирование глобального вектора узловых сил).

7.Учет граничных условий.

8.Определение узловых перемещений конструкции в общей системе координат.

9.Определение внутренних узловых усилий и напряжений в отдельных элементах конструкции.

Решение приведенных ниже задач выполняется по описному выше алгоритму. В отдельных задачах некоторые пункты могут не использоваться.

48

4.2. Расчет статически определимой балки МКЭ

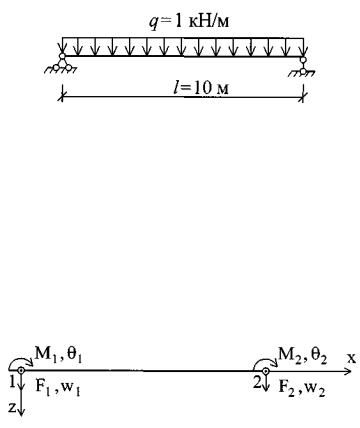
Рассмотрим простую шарнирно опертую балку постоянного сечения (ЕJ = const) длиной l = 10 м, загруженную равномерно распределенной нагрузкой q = 1 кН/м (рис. 4.1).

Рис. 4.1. Расчетная схема

Требуется определить узловые перемещения и построить эпюру прогибов и изгибающих моментов. И

4.2.1. Расчет балки, представленной одним конечным элементом

узлами, с 4 степенями свободы (по двеДв каждом узле) и с заданным направлением глобальныхбосей (рис. 4.2).

1. Рассмотрим балку в видеАодного конечного элемента с двумя

иР с. 4.2. Конечный элемент балки

2. Локальная матрица жесткости имеет размерность 4×4 (коли-

3. Коэффициенты матрицы жесткости определяются по формуле

(2.23):

kij = ∫0lEJ × Ni" (x) × N"j (x)dx ,

49

где Ni" (x), N "j (õ) – вторые производные функций формы в i-м и j-м

единичных состояниях (i, j =1,…,4), определяемые выражениями

(2.19).

Функция прогибов задается выражением (2.2):

w(x) = N1(x)∆1 + N2(x)∆2 + N3(x)∆3 + N4(x)∆4 ,

где Ni(x) –координатные функции, определяемые выражениями (2.3);

∆ i – неизвестные узловые перемещения (i = 1,…,4).

Рассмотрим вычисление одного из коэффициентов локальной

4. Поскольку конструкция представлена одним конечным элементом, глобальная матрица жесткости совпадает с локальной:

[K ]= [k ].

5.Вектор узловых сил имеет размерность 1×4 (совпадает с числом степеней свободы балочного элемента):

50

где Fi – узловые силы, определяемые по формуле

Рассмотрим вычисление одного компонента вектора {F}:

6. Так как конструкция представлена одним конечным элементом, то глобальный вектор узловых сил {P} совпадает с локальным:

51

{P}= {F}.

7. Определим номера степеней свободы в глобальной системе, в которых перемещения отсутствуют. Это номера 1 и 3. В глобальной матрице жесткости столбцы и строки с данными номер ами вычеркиваются или обнуляются:

или после учета гран чных условий (перемещения отсутствуют) размерность задачи уменьшается:

9. Для решения системы уравнений можно применять метод Гаусса, Холецкого, Зейделя и др. После решения системы уравнений (4.4), получаем значения узловых перемещений:

52