Министерство образования и науки РФ Федеральное государственное бюджетное образовательное учреждение высшего образования
«Сибирская государственная автомобильно-дорожная академия (СибАДИ)»
Кафедра «Строительная механика и геотехнологии»
|
|
Д |
|
ОСНОВЫ МЕТОДА КОНЕЧНЫХИ |
ЭЛЕМЕНТОВ |
||
|
б |
|
|
и |
|
|
|
Уче ноеАпособие |
|
||
С |
|
|
|
Омск ▪ 2016
УДК 624+539.3 |
Согласно 436-ФЗ от 29.12.2010 «О защите детей от информации, |
||
причиняющей вред их здоровью и развитию» данная продукция |
|||
ББК 38.112 |
маркировке не подлежит. |
|
|
М54 |
Рецензенты: |
||
|
|||
|
д-р физ.-мат. наук, проф. Г.Л. Горынин (СурГУ); |
||
|
канд. техн. наук, доц. В.Е. Русанов (СибАДИ) |
||
Работа утверждена редакционно-издательским советом СибАДИ в качестве учебного пособия. |
|||
|
СибАДИ |
||
М54 Основы метода конечных элементов [Электронный ресурс] : учебное пособие / С.А. Матвеев, О.П. Лаптев, Е.А. Мартынов,
Н.Н. Литвинов. – Электрон. дан. − Омск : СибАДИ, 2016. – URL: http://bek.sibadi.org/cgi-bin/irbis64r_plus/cgiirbis_64_ft.exe. - Режим доступа: для авторизованных пользователей.
ISBN 978-5-93204-933-4.
Содержит теоретический материал по основам метода конечных элементов: построение матриц жесткости, векторов узловых сил, построения общих систем уравнений. Приведены примеры расчета балок МКЭ и задания для самостоятельной работы.
Имеет интерактивное оглавление в виде закладок.
Предназначено для аспирантов направления 08.06.01 «Техника и технология строительства» и магистрантов направления 08.04.01 «Строительство».
Текстовое (с мвольное) издание (1,3 МБ)
Системные требования : Intel, 3,4 GHz ; 150 МБ ; Windows XP/Vista/7 ; DVD-ROM ;
1 ГБ свободного места на жестком диске ; программа для чтения pdf-файлов Adobe Acrobat Reader ; Google Chrome
Редактор Т.И. Калинина
Техническая подготовка − Т.И. Кукина Издание первое. Дата подписания к использованию 29.06.2016
Издательско-полиграфический центр СибАДИ. 644080, г. Омск, пр. Мира, 5 РИО ИПЦ СибАДИ. 644080, г. Омск, ул. 2-я Поселковая, 1
© ФГБОУ ВО «СибАДИ», 2016
ВВЕДЕНИЕ
Метод конечных элементов (МКЭ) относится к современным методам численного анализа. МКЭ получил свое развитие в середине XX века. В начальной фазе он развивался по двум независимым один от другого путям – вначале инженерному, а затем математическому. Для развития МКЭ особое значение имели вариационные принципы строительной механики сплошной среды и математические методы, которые развивались на основе этих принципов. Два подхода позднее слились в один общий, что имело огромное значение для дальнейшего быстрого развития МКЭ и его широкого применения.
конечных элементов" ввел в 1960 г. Клоуг. С этого времени начина-
Появление ЭВМ стимулировало развитие МКЭ, основы которого были сформулированы Р. Курантом вИ1943 г. Название "Метод
ется значительный рост числа работД, посвященных вопросам МКЭ.
Появление монографии Зенкевича и Ченга позволило подробно рас-
крыть основы метода и расширить области практического примене-
правлены на проблемы аппроксимациибА(разбиения) и конвергенции (точности) решений.
ния почти для всех задач механики сплошной среды, имеющих ва-
риационную формулировку. Дальнейшие работы ученых были на-
Период последнихидесяти лет особенно характерен для развития и применения МКЭ в таких о ластях линейной и нелинейной механики сплошнойСсреды, как геометрическая и физическая нели-
нейность, динамика конструкций, термодинамика, оптимизация конструкций и др.
МКЭ в настоящее время является одним из наиболее популярных методов численного моделирования, применяемых при проектировании инженерных сооружений. Имеющиеся в настоящее время современные программы для ЭВМ с высокой степенью автоматизации, например COSMOS(США), ЛИРА (Украина), BASYS(Россия) ТС Midas, Z_Soil (Швейцария) и др., позволяют создавать новые условия для анализа и расчета сложных инженерных конструкций.
МКЭ относится к методу дискретного анализа. Вместо всего тела основу всех исследований составляет часть области конечных размеров или конечный элемент. Тело, как сплошная среда с бесконечно многими степенями свободы, заменяется дискретной моделью связанных между собой конечных элементов с конечным числом
3
степеней свободы. Поскольку дискретных моделей может быть выбрано большое множество, то основная задача сводится к выбору модели, лучше всего аппроксимирующей расчетную область.
Основные классические зависимости между геометрическими и физическими величинами применяются на элементе дифференциально малых размеров. Зависимости между средними значениями этих величин, предполагая их непрерывность, распространяются с бесконечно малых элементов на всю рассматриваемую область. Таким образом, процесс описания явления сводится к дифференциальным уравнениям обычным или частным, интегральным или инте- грально-дифференциальным. При этом необходимо заметить, что решение в закрытой форме, особенно частных интегралов и диффе-
ренциалов, весьма сложно, поэтому решение сводится к поиску их |
||
приближенных решений. |
|
И |
|
|
|
Алгоритм расчета МКЭ можно представить в виде последова- |
||
тельности следующих шагов: |
Д |
|
|
|
|
-дискретизация сплошной среды; |
|
|
-выбор интерполирующих функций; |
|
|
-вычисление характеристик элементов; |
||
-формирование уравнений для сетки конечных элементов; |
||
-решение системы уравнений; |
|
-анализ напряженно-деформированного состояния. |
|
|
и |
Первые три шага осо енноАважны. Способ дискретизации, вы- |
|
бор типа элемента |
о щего числа элементов зависит от природы |
С |
|
решаемой задачи |
необходбмой точности решения. Вместе с тем |
наряду с выбором ч сла т па элементов важен выбор количества степеней свободы в узле, а также вида интерполирующего полинома.
Последние шаги имеют большое значение для практических расчетов. В данной области продолжаются исследования, связанные, прежде всего, с уменьшением времени счета при решении больших систем алгебраических уравнений.
В зависимости от способа выбора неизвестных в узлах различают три основных вида МКЭ в следующих формах: метод перемещений; метод сил; смешанный или гибридный метод.
В данном учебном пособии рассматривается МКЭ в форме метода перемещений.
Существующая литература по МКЭ[1–7] в большей своей части ориентирована на специалистов, уже знакомых с основами метода. В данном
4
пособии сделана попытка изложения основ МКЭ для начинающих изучение метода конечных элементов. При этом перед авторамистояла цель объединить в одном пособии и систематизировать материал, имеющийся в различных источниках и позволяющий в наиболее доступном виде изложить основные идеи МКЭ в форме метода перемещений на простых одномерных типах конечных элементов: стержневых и балочных. При этом большое внимание уделено разъяснению механического смысла коэффициентов жесткости, построенному на использовании расчетных схем метода перемещений из классического курса строительной механики. На наш взгляд, это должно облегчить восприятие МКЭ, поскольку в учебных программах курса строительной механики ему предшествует метод перемещний.
Преследуя методические цели, авторы на примере простейших конечных элементов изложили два способа получения разрешающих уравнений МКЭ, которые основаны на наиболее общих вариационных принципах – принципе возможных перемещений и принципе минимума потенциальной энергии.
В пособии изложены такие существенные вопросы, как процедура
формирования глобальной матрицы жесткости и вектора свободных членов |
||
|
|
И |
при узловом и внеузловом приложении нагрузки, а также учет граничных |
||
|
|
Д |
условий. Излагаются основные принципы расчета простейших одномерных |
||
|
б |
|
балочных конструкций, работающих на изгиб. |
||
Данное пособие написано на основе курса лекций, в течение ряда лет |
||
и |
|
|
читаемого студентам строительныхАспециальностей в Сибирской государ- |
||
ственной автомобильно-дорожной академии (СибАДИ). |
||
С |
|
|
5
1.КОНЕЧНЫЕ ЭЛЕМЕНТЫ
ИРАЗРЕШАЮЩИЕ УРАВНЕНИЯ
1.1. Идея метода перемещений
При расчете конструкции МКЭ рассматриваемое тело делится на конечное число малых частей – конечных элементов (КЭ), связанных между собой в определенном числе точек – узлах. Если предположить, что перемещения в любой точке конечного элемента можно выразить в зависимости от перемещений в узлах, то задача сводится к вычислению перемещений в узлах. Перемещения узлов области и на контуре определяются системой уравнений, которые представляют собой условия
равновесия узлов, а также условия на контуре. Эти уравнения могут быть |
||
|
|
И |
сформированы несколькими путями, в том числе на основе принципа ми- |
||
нимума потенциальной энергии. |
|
|
1.2. Дискретизация (разбиение) расчетной схемы |
||
|
А |
|
Сущность дискретизации (разбиения) тела по МКЭ состоит в |
||
следующем: |
|
|
-рассматриваемое тело с помощьюДвоображаемых линий или |
||
поверхностей разбивается на элементы конечных размеров. Эти |
||
элементы называются конечными элементами, а их совокупность – |
|
сеткой конечных элементов; |
|
|
С |
-конечные элементыбсоединены в конечном числе точек, кото- |
|
рые находятся на контуре элемента и называются узловыми точками |
|
или узлами; |
и |
-состояние каждого конечного элемента (перемещение, деформация, напряжение и т.д.) описывается с помощью интерполирующих функций и конечного числа параметров в узлах (степеней свободы), представляющих основные неизвестные МКЭ (рис. 1.1).
Число узловых перемещений и соответствующих им узловых сил равно числу степеней свободы. Числом степеней свободы называют количество независимых параметров, определяющих положение в пространстве узловой точки конечного элемента и всей дискретной расчетной схемы конструкции. В соответствии с этим различают количество степеней свободы одного узла mу, конечного элемента mэ и всей конструкции m. Если вся расчетная схема имеет n узлов, то общее число степеней свободы определяется по формуле
6
m = n my. |
(1.1) |
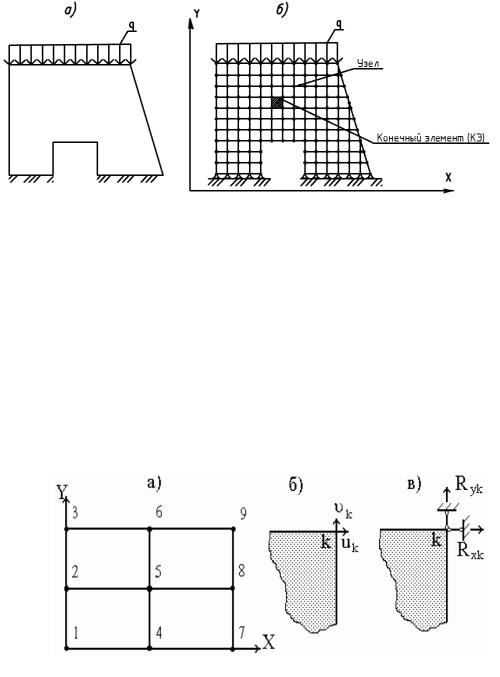
Рис. 1.1. Плоская расчетная схема (а) и ее конечно-элементное представление (б)
четыре прямоугольных элемента. Каждая узловаяИточка на плоскости имеет две степени свободы. В качестве степеней свободы произвольной точки k (рис. 1.2,б) рассматриваются линейные
Степени свободы имеют определенный физический смысл.
Они представляют собой узловые перемещения.
На рис. 1.2 представлен пример плоской области, разбитой на
перемещения этой точки ик и vк соответственно в направлении осей X |
||||
|
|
|
|
Д |
и Y. Таким образом, количество степеней свободы одного узла равно |
||||
двум: my = 2. |
|
|
А |
|
|
|
|
||
|
|
б |
|
|
|
и |
|
|
|
|
С |
|
|
|
Рис.1.2. Конечно-элементная дискретизация области
Так как один прямоугольный конечный элемент содержит четыре узла, то количество степеней свободы такого элемента равно восьми: тэ = 8. Соседние конечные элементы могут иметь общие узлы.
Полное количество узлов расчетной схемы, представленной на рис. 1.2,а, равно девяти: n = 9. Общее количество степеней свободы всей системы т = n ту = 9×2 = 18.
7