3.3. Учет граничных условий

При работе любой конструкции необходимо учитывать условия ее опирания, или так называемые граничные условия. На первом этапе конечно-элементной дискретизации конструкции на узловые перемещения не накладывается никаких ограничений. Учет граничных условий является следующим этапом. При этом на расчетную схему накладываются дополнительные связи по направлению тех степеней свободы, узловые перемещения которых необходимо исключить в соответствии с условиями опирания конструкции. Так, на схемах (а) и (в) (см. рис. 3.4) опорные связи накладываются по направлению 1-й и 2-й степеней свободы, на схемах (б) и ( г) – по на-

общей системы уравнений, в результате которого решение преобра-

зованной системы даёт нулевые перемещения по направлению заданных опорных связей. Изложим три способа учета граничных условий.

вых перемещений. ПредварительнобАвсе уравнения в общей системе (1.15) должны бытьипронумерованы в соответствии с общей нумерацией всех узловых перемещений системы. Затем должны быть установлены номераСнулевых узловых перемещений. Далее, из общей матрицы жесткости нужно сключить строки и столбцы, номера ко-

При первом способе из общей системы уравнений исключают-

ся уравнения с номерами, совпадающими с номерами нулевых узло-

торых совпадают с номерами нулевых перемещений, а из вектора свободных членов – элементы с теми же номерами.

Так, для всех балок, изображённых на рис. 3.4, система уравнений (1.15) принимает вид:

При первом способе учета граничных условий общая система уравнений (3.11) для схемы, представленной на рис. 3.4,а, преобразуется к виду

кращение размерности преобразованной системы уравнений по сравнению с размерностьюбисходной системы.

К недостаткам спосо а можно отнести затраты, связанные с перенумерацией элементовипрео разованной матрицы жесткости и

вектора свободных членов, а также переход от полученного вектора решения преобразованнойС с стемы к вектору узловых перемещений в исходной системе координат.

При втором способе преобразование общей системы уравнений выполняется без изменения её размерности.

Пусть задано перемещение ∆i = 0, тогда i-я строка и i-й столбец в общей матрице жесткости заменяются нулями, коэффициент жесткости, стоящий на главной диагонали Кii = 1, а свободный член Pi = 0. Таким образом, вместо вычеркнутого уравнения с номером i

После решения уравнения (3.11) получим

При втором способе приходится решать систему уравнений большей размерности, чем при первом, но зато нет необходимости выполнять перенумерацию элементов матрицы жесткости и вектора свободных членов.

При третьем способе учета граничных условий преобразования исходной системы − самые минимальные. Заключаются они в том, что для выполнения условия ∆i = 0 в уравнение (3.15) нужно подставить значение Кii = ∞, не меняя при этом других коэффициен-

Особенностью МКЭ является то, что главный коэффициент Кii

всегда положителен и принимает наибольшее значение среди коэф-

метод исключения Гаусса, метод Холецкого, метод Гаусса - Зейделя и др.

В результате решения системы уравнений (1.15) находим узловые перемещения ∆1, ..., ∆т , формирующие вектор {∆} в общей системе отсчета. Зная узловые перемещения, легко определить перемещения w(x) и θ(х) внутри любого конечного элемента по формулам:

i=1

Здесь Ni′(x) − первая производная i-й функции формы

44

основной зависимостью теории изгиба (2.14):

Рассмотрим конкретный пример. Пусть требуется определить перемещения и изгибающий момент в сеченииk балки, изображённой на рис. 3.5,а. Это сечение расположено в пределах второго конечного элемента.

Нагрузка на балку может быть произвольной. В результате выполнения процедуры формирования глобальной матрицы жесткости и вектора свободных членов, учета граничных условий и решения системы уравнений в форме (1.17) имеем вектор узловых перемещений {∆}.

Перемещения и изгибающий момент в сечении k определяем по формулам (3.18) и (3.23). Но прежде чем воспользоваться этими формулами, необходимо помнить, что они записаны для местной системынумерации степеней свободы (см. рис. 3.5,б). Узловые перемещения, найденные в результате решения системы уравнений, получены в общей системе

45

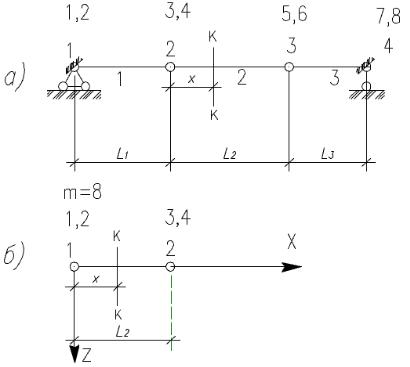
отсчёта. Рассматриваемая балка разбита на 3 конечных элемента с полным числом степеней свободы m = 8. Поэтому в общей системе отсчета имеем 8 узловых перемещений: ∆1 , . . . , ∆8 . Перемещения и изгибающий момент в сечении k определяем по формулам (3.18) и (3.23), изменив в них узловые перемещения в местной системе нумерации узловыми перемещениями, записанными в общей системе отсчёта:

M(х) = - EJ [∆3N˝1(x) + ∆4N˝2(x) + ∆5 N˝3(x) + ∆6 N˝4(x)].

Рис. 3.5. Общая (а) и местная (б) системы нумерации узлов и степеней свободы 2-го конечного элемента

Если учесть, что функции формы N1(x),..., N4(x) описываются выражениями (2.3), представляющими собой кубические полиномы, то эпюра прогибов балочного элемента будет иметь вид кубическойпараболы. Соответственно эпюра углов поворота θ будет иметь очертание квадратной параболы в пределах одного конечного элемента. Вторые производные функций формы N˝1(х),...,N˝4(x) описываются выражениями (2.22). Они являются линейными функциями координаты х, следовательно, линейной в пределах одного конечного элемента будет и зависимость М(х). Это приводит к тому, что очертание эпюры изгибающих моментов в пределах

46