
- •ВВЕДЕНИЕ
- •1.1. Идея метода перемещений
- •1.2. Дискретизация (разбиение) расчетной схемы
- •1.3. Типы конечных элементов
- •Вопросы для самопроверки
- •2. ВЫВОД РАЗРЕШАЮЩИХ УРАВНЕНИЙ МКЭ
- •2.1. Аппроксимация перемещений на элементе
- •2.2. Общие требования к аппроксимирующим функциям перемещений и рекомендации по их применению
- •2.3. Механический смысл коэффициентов жесткости
- •2.4. Определение коэффициентов жесткости из принципа возможных перемещений
- •2.5. Приведение нагрузки на элементе к узловой
- •2.6. Вывод разрешающих уравнений МКЭ из принципа минимума полной потенциальной энергии
- •Вопросы для самопроверки
- •3. ПОСТРОЕНИЕ ОБЩЕЙ СИСТЕМЫ УРАВНЕНИЙ
- •3.1. Глобальная матрица жесткости
- •3.1.1. Плоская задача
- •3.1.2. Изгиб балки
- •3.2. Вектор свободных членов
- •3.3. Учет граничных условий
- •3.4. Определение перемещений и усилий в балке
- •Вопросы для самопроверки
- •4. ПРИМЕРЫ РАСЧЕТА БАЛОК
- •4.1. Общая схема алгоритма расчета МКЭ
- •4.2. Расчет статически определимой балки МКЭ
- •4.2.1. Расчет балки, представленной одним конечным элементом
- •4.2.2. Расчет балки, разбитой на два конечных элемента
- •4.3. Расчет статически неопределимой балки МКЭ
- •4.4. Задания к самостоятельной работе
- •Библиографический список
где {∆} – вектор узловых перемещений размерности т; {P} – вектор узловых нагрузок размерности т; [К] – глобальная матрица жесткости
т×т.
Вопросы для самопроверки
1.В чем заключается идея метода конечных элементов?
2.Какие бывают виды конечных элементов?
3.Как определяется число степеней свободы конечного элемента?
4.В чем состоит сущность дискретизации системы?
5.Чем локальные координаты отличаются от глобальных?
6.В чем физический смысл коэффициента k11 в матрице жесткости?
7.Как записывается зависимость между векторами узловых перемещений и узловых нагрузок? ИД
|
|
А |
|
б |
|
и |
|
|
С |
|
|
16
2. ВЫВОД РАЗРЕШАЮЩИХ УРАВНЕНИЙ МКЭ
2.1. Аппроксимация перемещений на элементе
Функции, с помощью которых определяются перемещения между узловыми точками внутри элемента, называются интерполирующи-
миили аппроксимирующими функциями, или функциями формы.
От выбора интерполирующих функций зависит выполнение условий непрерывности функции и ее производных между отдельными элементами, а следовательно, точность решения.
Рассмотрим балочный элемент, который представлен в табл. 1.1 (тип II). Он имеет четыре степени свободы (mэ= 4).
Для приближенного описания перемещений внутри данного конечного элемента используется идея метода Ритца, в соответствии с которой неизвестная функция перемещений w(х) заменяется куби-
ческим полиномом с постоянными коэффициентами ai: |
|
|
w(х)=a1 + a2 x +a3 x2 + a4 x3. |
(2.1) |
|
|
И |
|
Коэффициенты ai не имеют физического смысла, а выражение |
||
Д |
|
|
А |
|
|
(2.1) называется представлением функции прогибов в неявной фор- |
||
ме. Функция прогибов в явной форме более удобна, так как коэффи- |
||
циенты ai в ней заменены имеющими физический смысл узловыми |
|||
перемещениями ∆i: |
б |
|
|
|
N3(x)+ ∆4 N4(x), |
(2.2) |
|
w(х)= ∆1N1(x) + ∆2 N2(x) +∆3 |
|||
|
и |
|
|
где N1(x),…, N4(x) – функции формы, представляющие собой одномерные полиномы Эрмита.
С |
|
x2 |
|
|
|
|
|
|
x3 |
|
|
2 |
|
3 |
|
|
||||||
N1(x) |
=1−3 |
|
|
|
|
|
+ 2 |
|
|
|
|
|
=1−3ξ |
|
+ 2ξ |
|
; |
|
||||
|
l2 |
|
l3 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
N2 (x)=1− 2 |
|
x2 |
|
+ |
|
x3 |
|
|
= x(1− 2ξ +ξ2 ); |
(2.3) |
||||||||||||
|
l |
|
|
l2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
N3 |
(x)= 3 |
x2 |
|
− 2 |
x3 |
|
= 3ξ2 − 2ξ3; |
|
|
|
||||||||||||
l2 |
l3 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
N4 (x)= − |
x2 |
|
|
+ |
x3 |
|
= −x(ξ −ξ2 ), |
|
|
|
||||||||||||
l |
|
|
l2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где ξ = x / l – безразмерная координата.
17
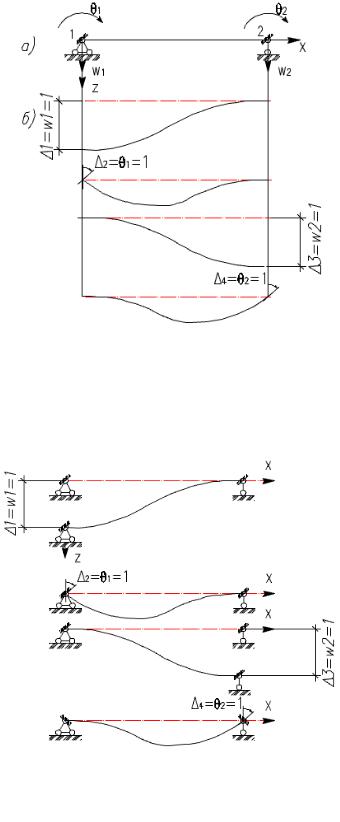
Эпюры функций формы представлены на рис. 2.1,б.
|
|
|
|
И |
|
|
Рис. 2.1. Балочный элемент (а) |
||
|
|
и эпюры функций формы (б) |
||
|
|
|
А |
|
Эти функции формы полностью совпадают с единичными |
||||
|
|
б |
|
|
эпюрами перемещений балки в основнойДсистеме метода перемеще- |
||||
ний (рис. 2.2). |
и |
|
|
|
|
|
|
||
С |
|
|
|
|
Рис. 2.2. Единичные состояния балочного элемента в основной системе метода перемещений
18
2.2.Общие требования к аппроксимирующим функциям перемещений и рекомендации по их применению
Для приближенного описания перемещений внутри конечного элемента используется идея метода Ритца, в соответствии с которой неизвестная функция перемещений w(x) заменяется суммой:
w(x) = ∑ai fi (x) |
(2.4) |
или |
|
w(x) = ∑∆i Ni (x) , |
(2.5) |
где ai – неизвестные коэффициенты, не имеющие определенного физического смысла; fi(x) – базисные функции, выбираемые с учетом требований и рекомендаций, сформулированных ниже; i – неизвестные коэффициенты, имеющие физический смысл узловых перемещений; Ni(x) – координатные функции, описывающие перемещения внутри конечного элемента, возникающие от единичных смещений
узлов. |
|
И |
|
|
|
Каждая координатная функция Ni(x) должна удовлетворять |
||
|
Д |
|
|
А |
|
уравнениям неразрывности в пределах конечного элемента и кинема- |
||
тическим граничным условиям в узлах. Следовательно, функции Ni(x) |
||
зависят от формы конечного элемента и поэтому они называются функциями формы.
В качестве пр мера баз сных функций и функции формы можно |
||||||||||
|
б |
|
|
|
|
|
|
|
||
рассмотреть функц , содержащиеся в выражениях (2.4) и (2.5), опи- |
||||||||||
и |
|
|
|
|
|
|
содер- |
|||
сывающих прогибы балочного элемента. В выражении (2.4) |
||||||||||
жатся следующие базисные функции: |
|
|
|
|
|
|
|
|||
f = 1; |
f |
2 |
= х; |
f |
3 |
= х2; |
f |
4 |
= х3. |
(2.6) |
С1 |
|
|
|
|
|
|
|
|||
В выражении (2.5) содержатся функции формы N1(x), N2(x), N3(x), N4(x), определяемые по формулам (2.3). Заметим, что для стержня постоянного сечения полученные функции формы являются точными.
Прямое определение функции формы, как в только что рассмотренных примерах, возможно лишь для простейших (стержневых) конечных элементов, поэтому в общем случае для трехмерных элементов используют следующий прием:
19
функции перемещений u(x,y,z), v(x,y,z),w(x,y,z), составляющие вектор {Z}, аппроксимируют в виде
{Z} =[ f ]{a}, |
(2.7) |
|
|
где {Z} – вектор перемещений, |
|
u(x, y, z) |
|
{Z}= v(x, y, z) ; |
|
w(x, y, z) |
|
|
|
[f] – матрица базисных функций fi(x,y,z); {a} – вектор коэффициентов |
||
ai, i = 1…S. |
|
|
Здесь S – число коэффициентов, как правило, равное числу сте- |
||
пеней свободы конечного элемента mэ. |
|
|
Требования к аппроксимирующим выражениям перемещений. |
||
|
|
И |
1. Функции {Z} должны удовлетворять уравнениям совместно- |
||
|
Д |
|
сти деформаций в пределах элемента либо, что предпочтительнее, |
||
разрешающим дифференциальнымАуравнениям в перемещениях для элементов данного т па (при нагрузках, прикладываемых только в уз-
лах). Например, для балочного конечного элемента функция прогибов |
||||
|
б |
|
|
|
w(x) должна удовлетворять уравнению |
|
|||
и |
d 4w |
|
|
|
С |
|
= 0 |
, |
|
|
dx4 |
|||
|
|
|
||
|
|
|
|
|
а для элемента изгибаемой тонкой изотропной плиты постоянной толщины приближенное выражение прогибов w(x,у) должно удовлетворять однородному (при q = 0) уравнению
4w = 0.
Если аппроксимировать функции w(x) и w(x,у) полиномами до третьей степени включительно, то указанные требования выполняются при любых коэффициентах ai.
20
2.Вычисленные по функциям {Z} деформации {ε} не должны быть тождественно нулевыми.
3.Функции {Z} должны удовлетворять кинематическим граничным условиям в узлах элемента, то есть при подстановке в {Z} координат узлов должно получаться значение узловых перемещений i. Из этого следует, что S (число коэффициентов а) должно быть не
менее суммарного числа степеней свободы узлов конечного элемента mэ (обычно S= mэ).
Кроме перечисленных требований при построении аппроксимации желательно учитывать следующие рекомендации:
1. По возможности выбирать базисные функции так, чтобы {Z} получались инвариантными к преобразованиям системы координат
элемента (параллельному переносу и повороту осей). Это достигается, в частности, использованием полных полиномов.
иметь на границе одинаковые перемещенияИ. Элементы, удовлетворяющие сформулированным условиям, называются совместными по
2. Следует стремиться к тому, чтобы по граням элемента перемещения, определяемые функциями {Z}, получались бы однозначно
зависящими от смещений узлов. Тогда два смежных элемента будут
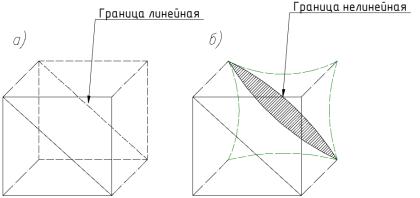
перемещениям, в противном случае – несовместными. На рис. 2.3,а |
|||
|
|
|
Д |
приведен пример совместных по перемещениям конечных элементов, |
|||
а на рис. 2.3,б – несовместных. |
|
||
|
|
А |
|
|
б |
|
|
и |
|
|
|
С |
|
|
|
Рис. 2.3. Совместные (a) и несовместные (б) конечные элементы
Сплошными линиями на рис. 2.3 изображены два смежных элемента в недеформированном состоянии, а штриховыми – в деформированном. В случае совместных элементов поля перемещений приняты линейными, о чем свидетельствует прямолинейность сторон де-
21
