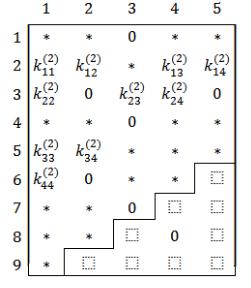
Рис. 3.2. Двумерный массив
И элемента в общей системе отсчётаА(последняя цифра первой строки
ется следующим образом. Номер четвёртого узла первого конечного
Если исходная область разбивается на прямоугольные конечные элементы, то ширина полулентыДматрицы жесткости определя-
табл. 3.1) умножается на количество узловых перемещений одного узла. Для схемы, представленной на рис. 3.1,а, номер четвёртого узла первого элемента равенб5, количество узловых перемещений т =2, следовательно, ширина полуленты равна 5×2 = 10.
у и3.1.2. Изгиб балки
Рассмотрим формирование глобальной матрицы жесткости на
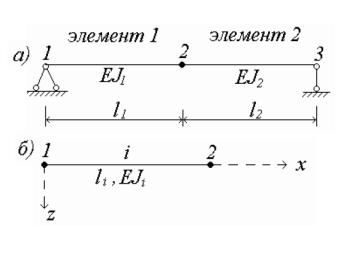
при расчёте балки (рис. 3.3,а).
Локальная матрица жесткости произвольного балочного эле- |
||||||||||||||
мента (рис. 3.3,Сб) имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
6 |
3l |
− 6 |
3l |
|
|
|
|
|
||||
[ k (i) ]= d i |
|
3l |
2l |
2 |
−3l |
l |
2 |
|
|
|
2 EJi . |
|
||
|
|
|
|
|
; |
di = |
(3.4) |
|||||||
|
− 6 −3l |
6 −3l |
|
|
l i3 |
|
||||||||
|
|
3l |
l |
2 |
−3l |
2l |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
Локальную матрицу жесткости балочного конечного элемента (3.4) можно представить в блочном виде по аналогии с матрицей
(3.1):
37
|
(i) |
|
|
(i) |
] |
(i) |
|
|
[k |
|
|
[k11 |
[k12 ] |
(3.5) |
|||
|
]= [k (i) |
] |
[k (i)] . |
|||||
|
|
|
|
21 |
|
|
22 |
|
|
|
|
|
|
|
|||
Элемент 1 |
|
|
|
|
Элемент 2 |
|
||
|
|
|
|
|
|
|
|
|
Рис. 3.3. Балка, разбитая на два элемента (а), и балочный элемент (б)
Число строк и число столбцов в матрице (3.5) определяется ко-
личеством узлов балочного элемента. |
Поскольку данный элемент |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
||||
имеет два узла (см. рис. 3.3,б), то число строк и столбцов равно двум. |
|||||||||||||||||
Блоки матрицы (3.5) с учетом (3.4) имеют следующий вид: |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
||
[k |
(i) |
]= d |
6 |
3li |
|
|
|
(i) |
|
− 6 |
|
3li |
; |
|
|||
|
i |
|
|
А; [k ]= d |
i |
|
|
2 |
|
||||||||
11 |
|
|
|
2 |
|
|
|
12 |
|
3li |
|
|
|
||||
|
|
|
3li |
2li |
|
|
|
|
|
− |
|
li |
|
(3.6) |
|||
|
|
|
|
б |
|
|
|
6 |
|
−3l |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
− 6 |
|
−3l |
|
|
|
|
|
|||||||
[k21(i)]= di |
3l |
|
l2 |
i |
; |
[k22(i)]= di −3l |
i |
2l2i |
. |
||||||||
|
|
иi |
i |
|
|
|
|
|
|
|
|
i |
|
||||
РазмерностьСкаждого из блоков 2×2, так как в каждом узле имеется по две степени свободы.
Матрицу преобразования можно записать либо в виде таблицы индексов степеней свободы, либо в виде таблицы узловых индексов. Табл. 3.2 узловых индексов балки, состоящей из двух элементов (рис. 3.3,а), составлена по аналогии с табл. 3.1 для плоской задачи и соответствует блочному представлению матрицы жесткости (3.4).
Матрица преобразования в виде таблицы индексов степеней свободы для этой же балки записывается в форме табл. 3.3 и соответствует обычному виду матрицы жесткости (3.3).
38
Таблица 3.2
Взаимосвязь индексов в системах отсчета
Номер элемента |
Узловые индексы в местной системе отсчета |
|
|
1 |
2 |
|
Узловые индексы в общей системе отсчета |
|
1 |
1 |
2 |
2 |
2 |
3 |
Таблица 3.3
Взаимосвязь индексов в системах отсчета
Номер |
Узловые индексы в местной системе отсчета |
|||||
1 |
|
2 |
3 |
|
4 |
|
элемента |
|
|
||||
|
Узловые индексы в общей системе отсчета |
|
||||
|
|
|
||||
1 |
1 |
2 |
И |
4 |
||
3 |
|
|||||
2 |
3 |
4 |
5 |
|
6 |
|
При составлении глобальной Дматрицы жесткости балки, состоящей из двух конечных элементов (см. рис. 3.3,а), представим локальные матрицы жесткости первого и второго конечных элементов схематично в следующем виде:
|
× |
× × × |
|
|
|
Ο |
Ο |
Ο |
Ο |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Ο |
Ο |
Ο |
Ο |
|
|||
[k(1)]= |
× × × ×А |
|
|
|
||||||||
× |
× × × |
; |
[k(2)]= |
Ο |
Ο |
Ο |
Ο . |
(3.7) |
||||
|
|
б |
|
|
|
|
|
|
|
|
||
|
× × × × |
|
|
Ο Ο Ο Ο |
|
|||||||
Размерность каждой из локальных матриц жесткости 4×4. |
|
|||||||
Учитывая матрицу преобразования в форме табл. 3.3, изобразим |
||||||||
схематично глобальнуюС |
матрицу жесткости всей балки в следующем |
|||||||
виде: |
× |
× |
× |
× |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
× |
× |
× |
× |
|
|
|
|
|
|
× |
|
|
Ο |
|
|
|
|
× |
Ο |
(3.8) |
|||||
[K]= |
× |
|
|
Ο |
Ο |
. |
||
|
× |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Ο |
Ο |
Ο |
|
|
|
|
|
|
Ο |
|
||||
|
|
|
Ο |
Ο |
Ο |
Ο |
|
|
39
Размерность глобальной матрицы 6×6, что соответствует общему числу степеней свободы всей балки (m = 6). Рассмотрим некоторые элементы третьей строки глобальной матрицы жесткости:
K32 |
(1) |
= − |
6 EJ1 |
; |
|
|
||
= k32 |
|
l 12 |
|
|
||||
|
|
|
|
|
|
|
|
|
K |
33 |
= k (1) |
+k (2) |
= 12 EJ1 |
+ 12 EJ2 ; |
(3.9) |
||
|
33 |
11 |
|
|
l 13 |
l 32 |
|
|
|
|
|
|
|
|
|
||
K |
34 |
= k (1) |
+k (2) |
= − 6 EJ1 |
+ 6 EJ2 . |
|
||
|
34 |
12 |
|
|
l 12 |
l 22 |
|
|
|
|
|
|
|
|
|
||
3.2. Вектор свободных членов
Вектор свободных членов общей системы уравнений МКЭ зависит от характера, места приложения и величины внешней нагруз-
ки, а также от степени дискретизации конструкции. Рассмотрим |
||||||||||||||
|
|
|
|
|
А |
|
|
|
|
|
|
|||
формирование вектора свободных членов наИконкретных примерах. |
||||||||||||||
Так, для всех балок, изображенных на рис. 3.4, количество ко- |
||||||||||||||
нечных элементов равно двум, количествоДузлов – трем, а колич ест- |
||||||||||||||
во степеней свободы – шести. Поэтому вектор свободных членов для |
||||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|||
всех этих конструкций состоит из шести элементов: |
|
|||||||||||||
С |
=б{P P P |
|
|
|
|
|
P }. |
|
||||||
{P}T |
P |
|
P |
(3.10) |
||||||||||
|
|
|
1 |
|
2 |
3 |
4 |
|
|
5 |
|
6 |
|
|
Ненулевыми элементами вектора (3.10) для схем, изображен- |
||||||||||||||
ных на рис. 3.4, являются следующие: |
|
|
|
|
|
|
|
|||||||
|
|
|
а) P5 |
= P , |
|
б) P1 |
= P; |
|
|
|||||
|
в) P6 |
= M , |
|
г)P2 |
= - М, P3 = P; |
(3.11) |
||||||||
|
|
|
|
д) P3 = P, P6 = М; |
|
|
|
|
||||||
|
|
ql |
|
|
|
q l |
2 |
|
q l |
1 |
|
|
q l 2 |
|
е) P |
= |
|
1 |
, P |
= |
|
1 , |
P = |
|
|
, |
P = |
1 . |
|
1 |
|
2 |
2 |
|
12 |
3 |
|
2 |
|
|
4 |
12 |
||
|
|
|
|
|
|
|
|
|
|
|||||
40
а) б)а)
в) г)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
А |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
б |
|
|
|
|
|
|||
|
|
|
да)) |
|
|
|
|
е) |
|
|||||
|
|
|
и |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
С |
|
|
|
|
|
|
|
|
|
||
Рис. 3.4. Формирование вектора свободных членов
41