
- •ВВЕДЕНИЕ
- •1.1. Идея метода перемещений
- •1.2. Дискретизация (разбиение) расчетной схемы
- •1.3. Типы конечных элементов
- •Вопросы для самопроверки
- •2. ВЫВОД РАЗРЕШАЮЩИХ УРАВНЕНИЙ МКЭ
- •2.1. Аппроксимация перемещений на элементе
- •2.2. Общие требования к аппроксимирующим функциям перемещений и рекомендации по их применению
- •2.3. Механический смысл коэффициентов жесткости
- •2.4. Определение коэффициентов жесткости из принципа возможных перемещений
- •2.5. Приведение нагрузки на элементе к узловой
- •2.6. Вывод разрешающих уравнений МКЭ из принципа минимума полной потенциальной энергии
- •Вопросы для самопроверки
- •3. ПОСТРОЕНИЕ ОБЩЕЙ СИСТЕМЫ УРАВНЕНИЙ
- •3.1. Глобальная матрица жесткости
- •3.1.1. Плоская задача
- •3.1.2. Изгиб балки
- •3.2. Вектор свободных членов
- •3.3. Учет граничных условий
- •3.4. Определение перемещений и усилий в балке
- •Вопросы для самопроверки
- •4. ПРИМЕРЫ РАСЧЕТА БАЛОК
- •4.1. Общая схема алгоритма расчета МКЭ
- •4.2. Расчет статически определимой балки МКЭ
- •4.2.1. Расчет балки, представленной одним конечным элементом
- •4.2.2. Расчет балки, разбитой на два конечных элемента
- •4.3. Расчет статически неопределимой балки МКЭ
- •4.4. Задания к самостоятельной работе
- •Библиографический список
2.5. Приведение нагрузки на элементе к узловой
Если внешняя нагрузка, действующая на элемент, приложена не в узловых точках, то ее необходимо заменить статически эквивалентными узловыми силами. Эти узловые силы формируют вектор
{Р}.
Для элемента, изображенного на рис. 2.4,в, вектор узловых сил
имеет вид |
|
|
|
|
|
|
R |
|
|
|
|
|
|
1P |
|
|
|
{P} |
R2P |
|
(2.28) |
||
= |
R |
. |
|
||
|
|
|
|
|
|
|
3P |
И |
|
||
|
R |
|
|
||
|
|
4P |
|
|
|
|
|
Д |
|
||
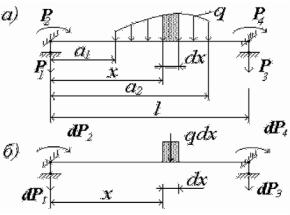
Для определения узловых сил воспользуемся теоремой о взаимности работ. Рассмотрим процедуру нахождения узловой силы Rlp. Для этого исследуем два состояния балочного элемента: единичное состояние 1 (рис. 2.4,а) и грузовое состояние Р (см. рис. 2.4,в).
В грузовом состоянии Р на балочный элемент действует сосредоточенная сила Р в сечении х = а и узловые силы, записанные в ви-
де вектора (2.28). Все узловые перемещения в грузовом состоянии |
||||
|
|
А |
|
|
отсутствуют, т.е. ∆j= 0 (j=1...4). |
1 на балочный элемент действуют |
|||
В единичном состоян |
|
|||
|
б |
|
||
только узловые с лы, зап санные в виде вектора (2.7). Перемещения |
||||
здесь следующие: ∆1 = 1, ∆2 = ∆3 = ∆4 = 0, а также |
|
|||
и |
|
|
|
|
С |
w(a) |
= N1(a). |
(2.29) |
|
|
|
|
|
|
Работа внешних сил состояния Р на соответствующих им пе- |
||||
ремещениях состояния 1 |
|
|
|
|
4 |
|
|
|
|
AP1 = ∑RiP ∆i + P w(a)= R1P ×1 + PN1(a). |
(2.30) |
|||
i=1 |
|
|
|
|
Работа внешних сил состояния 1 на соответствующих им узловых перемещениях состояния Р
27
4
A1P = ∑ri1 ∆i = 0 . (2.31)
i=1
Подставив соотношения (2.30) и (2. 31) в выражение теоремы взаимности работ (теоремы Бетти)
AP1 = A1P , |
(2.32) |
получим |
|
R1P = −PN1(a). |
(2.33) |
По аналогии может быть получена формула приведения |
|
сосредоточенной нагрузки на элементе к узловой: |
|
И |
|
R iP = −PNi (a), i = 1,…,4. |
(2.34) |
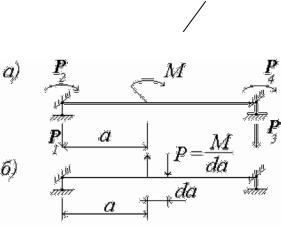
Для приведения распределенной нагрузки на элементе к узло-
вой (рис. 2.5,а) выделим бесконечно малый участок стержня длиной |
|
А |
q будем считать |
dx, в пределах которого распределённую нагрузку |
|
постоянной. Заменяя в пределах этого участка распределённую на- |
|||||
грузку элементарной сосредоточеннойДсилой, равной qdx (рис. |
|||||
2.5,б), воспользуемся формулой (2.34). В результате получим выра- |
|||||
и |
|
|
|
|
|
жение для элементарной узловой силы: |
|
|
|
||
С |
бdR = −qdxN |
(x). |
(2.35) |
||
|
|
iP |
i |
|
|
Рис. 2.5. Приведение распределенной нагрузки на балочном элементе к узловой
28
Полное значение узловой силы получим, интегрируя выражение
(2.35):
a2 |
|
R iP = − ∫qNi dx. |
(2.35) |
a1 |
|
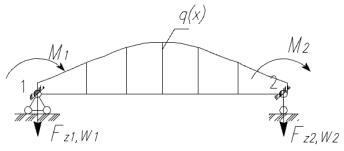
При действии на балочный элемент сосредоточенного момента в сечении х = а (рис. 2.6,а) заменим момент М двумя сосредоточенными силами Р, расположенными на расстоянии da одна от другой и направленными навстречу друг другу (рис. 2.6,б). Между силами и
моментом соблюдается зависимость P = M da .
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
Д |
|
||
|
|
|
А |
|
|
|
||
|
|
б |
|
|
|
|
||
Рис. 2.6. Приведение сосредоточенной |
|
|||||||
моментной нагрузки на балочном |
|
|||||||
|
|
элементе к узловой |
|
|||||
и |
|
|
|
|
|
|
||
Используя зав с мость (2.34) отдельно для каждой из сил, а |
||||||||
С |
|
|
|
|
|
|
|
|
затем суммируя, пр ход м к выражению |
|
|
|
|||||
R |
|
= M |
N |
(a) |
− M |
N |
(a +da). |
(2.37) |
|
iP |
da |
i |
|
da |
i |
|
|
Учитывая, что Ni (a +da)− Ni (a)= dNi и вводя обозначение |
||||||||
|
|
|
|
dNi |
= Ni′ |
, |
|
(2.38) |
|
|
|
|
da |
|
|
|
|
выражение (2.37) представим в следующем виде: |
|
|||||||
|
|
RiP |
= −M Ni′(a). |
|
(2.39) |
|||
|
|
|
|
29 |
|
|
|
|
2.6. Вывод разрешающих уравнений МКЭ из принципа минимума полной потенциальной энергии
Выражение полной потенциальной энергии балочного элемента (рис. 2.7) имеет вид
Π = |
1 l |
′′ 2 |
l |
(2.40) |
|
2 |
∫EJ (w ) |
dx − ∫q(x)w(x)dx. |
|||
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
И |
|
||||
|
|
|
|
|
|
Д |
|
|
|
|
|||
|
|
Рис. 2.7. Балочный конечный элемент |
|
||||||||||
Функцию прогибов аппроксимируем в явном виде: |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
∆1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
и |
|
|
|
|
|
|
2 |
|
|
|
|
w(x)= N |
∆ |
|
N |
N |
|
N |
|
] |
|
= [N ]{∆}. |
(2.41) |
||
+... + N ∆ |
= [N |
|
|
|
|
||||||||
1 1 |
4 4 |
1А2 |
3 |
|
4 |
∆ |
|
|
|||||
|
С |
б |
|
|
|
|
3 |
|
|
|
|||
|
|
|
|
|
∆ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
Продифференцировав дважды по х выражение (2.41), получим |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
∆1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
′′ |
′′ |
′′ |
|
′′ |
′′ |
|
′′ |
|
′′ |
2 |
|
|
|
|
|
|
] ∆ |
= [B]{∆}. |
(2.42) |
||||||||
w (x)= N1∆1 +...+ N4∆4 = [N1 |
N2 |
N3 |
N4 |
||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
Здесь [В] – матрица вторых производных функций формы |
|||||||||||||
|
|
[B]= [N1′′ |
|
N2′′ |
N3′′ |
|
N4′′]. |
|
|
|
(2.43) |
||
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
Первый интеграл из (2.40) запишем с учётом соотношения (2.42) в следующем виде:
∫l EJ (w′′)2dx = ∫l (w′′)EJ (w′′)dx =
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
N′′ |
|
|
|
|
|
∆ |
|
(2.44) |
||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
= ∫l {∆1 ∆2 |
∆3 ∆4 |
} N2′′ |
[D][N1′′ |
N2′′ |
N3′′ |
N4′′] ∆2 |
dx. |
|
||||
|
|
|
′′ |
|
|
|
|
|
∆3 |
|
|
|
0 |
|
N3 |
|
|
|
|
|
|
|
|
||
|
|
N4′′ |
|
|
|
|
|
∆4 |
|
|||
Здесь [D] – матрица упругости, состоящая из одного элемента: |
||||||||||||
l |
|
l |
|
|
|
|
И |
|
|
(2.45) |
||
|
|
|
[D]= EJ[1]= EJ . |
|
|
|
|
|||||
|
|
|
|
|
|
Д |
|
|
|
|
|
|
Интеграл (2.44) представим в матричном виде: |
|
|
|
|||||||||
∫EJ (w ) dx = |
∫{∆} |
А |
|
|
[k]{∆}, |
(2.46) |
||||||
[B] |
[D][B]{∆}dx ={∆} |
|||||||||||
|
′′ 2 |
|
Τ |
Τ |
|
|
|
Τ |
|
|
|
|
0 |
|
б |
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
где {∆}T и [Â]T |
– транспонированные вектор узловых перемещений и |
|||||||||||
матрица вторых про зводных соответственно: |
|
|
|
|
|
|||||||
|
и |
|
|
|
|
N1′′ |
|
|
||||
|
∆ |
∆ |
}; |
[Â]T |
|
′′ |
|
(2.47) |
||||
{∆}T ={∆ |
∆ |
= N2 ; |
|
|||||||||
|
1 |
|
2 |
3 |
4 |
|
N3′′ |
|
|
|||
С |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
N4′′ |
|
|
||||
[k] – матрица жесткости балочного элемента, определяемая по формуле
[k]= ∫l [B]Τ [D][B]dx. |
(2.48) |
0 |
|
После подстановки в выражение (2.48) соотношений (2.43), (2.45) и (2.47) и интегрирования с учетом зависимостей (2.22) получим матрицу жесткости балочного конечного элемента:
31
|
|
|
6 |
3l |
− 6 |
3l |
|
|
||||
[k ] = |
2 EJ |
|
3l |
2l |
2 |
−3l |
l |
2 |
|
|
||
|
|
|
|
. |
(2.49) |
|||||||
|
l 3 |
− 6 −3l |
6 −3l |
|
||||||||
|
|
|
3l |
l |
2 |
−3l |
2l |
2 |
|
|
||
|
|
|
|
|
|
|
|
|||||
Второй интеграл из (2.36) запишем с учетом соотношения (2.37) в следующем виде:
∫l |
q (x)w (x)dx = ∫l q (x)[N1(x)∆1 +.... + N4 (x)∆4 ]dx = |
|
||||||||
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
(2.50) |
|
|
|
|
|
1 |
|
|
|
И |
|
= ∫l q [N1 |
N2 N3 N4 |
] ∆∆2 |
dx |
= ∫l |
|
|||||
q [N ]{∆}dx. |
|
|||||||||
|
0 |
|
|
|
3 |
|
|
0 |
|
|
|
|
|
|
∆ |
|
Д |
|
|||
|
|
|
|
|
4 |
|
|
|
|
|
С |
учетом |
2 |
|
А |
(2.50) выражение полной |
|||||
соотношений |
|
(2.46) |
и |
|||||||
потенциальной энергии (2.40) можно представить в матричном виде: |
|||||
|
|
|
б |
|
|
|
|
Π = 1 |
{∆}Τ [k]{∆}+{P}Τ {∆}, |
(2.51) |
|
|
|
и |
|
||
|
С |
|
|
|
|
Τ |
|
|
|
|
|
где {P} |
– транспон рованный вектор узловых сил, |
|
|||
|
|
{P}T |
= − ∫l q [N ]dx . |
(2.52) |
|
|
|
|
|
0 |
|
Произвольная компонента вектора {Р} определяется по фор- |
|||||
муле |
Pi = − ∫l q (x)Ni (x) dx, i =1,...,4. |
|
|||
|
(2.53) |
||||
|
|
|
0 |
|
|
Из условия стационарности полной потенциальной энергии:
d Ï |
или |
∂ Ï |
= 0, i =1,..., m |
(2.54) |
|
|
= 0 |
∂∆ |
|||
d {∆} |
|||||
|
|
|
i |
|
|
|
|
|
|
32 |
|
