формированных элементов, а в случае несовместных – нелинейными, при этом между границами соседних элементов появляется зазор (заштрихованная область на рис. 2.3,б). В идеале элементы должны быть совместными не только по перемещениям, но и по деформациям и напряжениям, но добиться этого значительно сложнее.

2.3. Механический смысл коэффициентов жесткости

Прежде чем определять коэффициенты жесткости балочного элемента, выясним их механический смысл. Для этого рассмотрим балочный элемент с наложенными по направлению всех степеней свободы дополнительными связями. По направлению первой степени

Полученное равенство позволяет объяснить механический смысл коэффициентов жесткости, которые по существу являются ре-

22

акциями в дополнительно наложенных связях в основной системе метода перемещений:

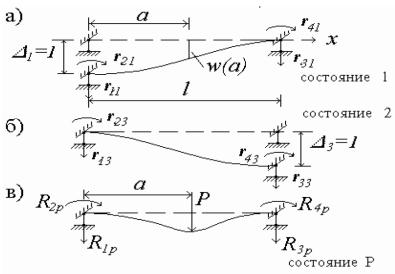
Рис. 2.4. Единичные (аД, б) и грузовоеИ(в) состояния балочного элемента

от единичного перемещенияб∆jА= 1. Каждый j-й столбец матрицы жесткости составлен из единичных реакций, соответствующих j-му единичному состоян ю элемента. Коэффициенты жесткости, представленные в выражен (2.7), соответствуют первому единичному со-

Каждый коэффициент kij представляет собой реакцию rij в дополнительно наложенной связи по направлению i-й степени свободы

2.4. Определение коэффициентов жесткости из принципа возможных перемещений

Рассмотрим два единичных состояния балочного элемента: состояние 1 (рис. 2.4,а) и состояние 3 (рис. 2.4,б). Состояние 1 примем за действительное, а состояние 3 – за возможное. Рассмотрим работу внешних и внутренних сил первого состояния на возможных перемещениях третьего состояния.

23

К внешним силам первого состояния относятся реактивные силы r11, r21, r31, r41. Они совершают работу на возможных узловых перемещениях ∆1, ∆2, ∆3, ∆4 третьего состояния. Но в третьем единичном состоянии ненулевым является только одно перемещение ∆3=1, остальные узловые перемещения нулевые: ∆1=∆2=∆4=0. Таким образом, возможная работа А13 реактивных сил состояния 1 на перемещениях состояния 3 равна:

4

A13 = ∑rj1∆j = r31∆3 = r31 . (2.12) j=1

Возможная работа внутренних сил состояния 1 на перемещениях состояния 3 определяется из выражения:

где М1 – изгибающий момент в балочном элементе в первом единичном

Из курса сопротивления материалов известна зависимость между изгибающим моментом Ми кривизной балкиρ при чистом изгибе:

Кривизну балки ρ заменяем второй производной функции прогибов ρ = w″. С учетом этой замены получим

24

Обозначим функцию прогибов в первом и третьем единичных состояниях как w1 и w3. Тогда вторые производные этих функций будут соответственно w″1 и w″3, а выражение (2.17), записанное для первого и третьего единичных состояний, примет вид

Подставляя в (2.21) узловые перемещения первого единичного состояния ∆1 = 1, ∆2 = ∆3 = ∆4= 0 и третьего единичного состояния

∆3 = 1, ∆1 = ∆2= ∆4 =0, получим

Принцип возможной работы в форме принципа возможных перемещений или вариационный принцип Лагранжа формулируется

25

так: если элемент твердого деформируемого тела находится в равновесии, то полная работа всех приложенных к нему сил на возможных перемещениях равна нулю. Следовательно, полная работа всех внешних и внутренних сил состояния 1 на возможных перемещениях состояния 3 должна быть равна нулю. При этом знак возможной работы внутренних сил берем «минус», так как рассматриваем процесс нагружения балки.

Из выражения (2.20) с учетом (2.12), (2.11) и (2.23) получим выражение для вычисления коэффициента жесткости k13:

При вычислении интегралов в формулах (2.24) и (2.26) необходимо произвести замену переменной интегрирования dx на dξ и пределов интегрирования [0, l] на [0,1]. При этом должно быть учтено равенство dx=ldξ .

Если в формуле (2.26) индексы i, j поменять местами, то результат не изменится. Это свидетельствует о том, что коэффициенты

а матрица жесткости симметрична относительно главной диагонали.

26