1055

в задаче несовместны, множество допустимых решений является пустым множеством, а задача поиска экстремума не имеет смысла.

2. Найти градиент целевой функции grad f c1i c2 j , построить

его.

3.Провести линию уровня целевой функции, перпендикулярную градиенту.

4.Перемещать линию уровня параллельно самой себе в направ-

прямых, пересекающихся в точке оптимума, вычислить fmax ( fmin). В случае непустого множества допустимых решений возможны

три типовых ситуации:

а) задача имеет единственное решение (линия уровня касается множества допустимых решений в одной точке);

б) задача имеет бесконечное множество решений (линия уровня касается множества допустимых решений вдоль стороны многоугольника);

в) задача не имеет решения (множество допустимых решений не ограничено).

Пример. Решить задачу линейного программирования

Решение. Построим область, определяемую системой (5)─(8). Нумеруем ограничения задачи. В прямоугольной декартовой системе координат строим прямую x1 x2 2, соответствующую ограничению (5). Находим, какая из двух полуплоскостей является областью решений неравенства. Так, прямая (5) не проходит через начало координат, подставляем координаты точки (0, 0) в первое ограничение 0 0 2. Получаем верное строгое неравенство 0 > -2. Следователь-

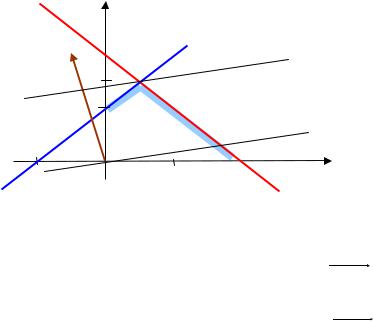
но, точка (0,0) лежит в полуплоскости решений. Аналогично строим прямые (6) ─(8) (рис. 1).

x2

Рис. 1. Область допустимых значений

Находим теперь градиент целевой функции grad f i 4j. Проводим линию уровня функции, перпендикулярную градиенту, передвигаем ее параллельно самой себе в направлении grad f . Эта прямая проходит через точку Х* пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (5) и

x1 x2 2;

(6). Определяем координаты точки Х*, решая систему

x1 x2 4.

Получаем Х*(1, 3). Вычисляем f (Х*) 6 1 4 3 5.

Ответ: fmax 5 в точке Х* (1, 3).

Задача линейного программирования не всегда задается в виде математической модели. Пример составления математической модели рассмотрен на примере транспортной задачи (раздел 3).

Вопросы для самопроверки

1.Какие методы решения задач линейного программирования вы знаете?

2.Какой смысл имеют дополнительные ограничения и целевая функция?

3.Объясните необходимость совместности ограничений в задачах линейного программирования.

4.Объясните существование множества решений в задачах линейного программирования.

Задача 1.24. Прибыль от изделий А, В, С составляет 3, 4, 5 единиц. Для каждого изделия требуется время использования станков I и II. Станки доступны 12 и 15 ч в день соответственно:

Найдите оптимальный план производства.

Задача 1.25. Два изделия В1 и В2 последовательно обрабатываются на станках № 1, 2, 3, 4, 5. Машинное время на единицу изделий на каждом станке указано в таблице. Здесь же приведена прибыль от каждого изделия, причем объем производства второго вида продукции не должен превышать 40 % общего выпуска. Определите оптимальную программу выпуска, обеспечивающую максимальную прибыль.

Решите задачу графически.

Задача 1.26. На предприятии могут изготавливать два вида продукции i1 и i2. На выпуск единицы продукции i1 расходуется 3 единицы ресурса, а на единицу продукта i2 – 1 единица того же ресурса. В плановом периоде в распоряжении предприятия имеется 300 единиц этого же ресурса. Ограничение по выпуску продукции первой и высшей категорий качества выглядит следующим образом:3x1 4x2 0. При этом требуется, чтобы продукции i1 было выпущено не менее 40 единиц. Предприятие желает получить максимальную прибыль.

Каждое изделие вида i1 дает 3 доллара прибыли, каждое изделие вида i2 дает 4 доллара прибыли. Решите эту задачу графически.

Задача 1.27. Средства очистки пола оценивают по следующим трем показателям: очищающие свойства; дезинфицирующие свойства; раздражающее воздействие на кожу. Каждый из этих показателей измеряется по линейной шкале от 0 до 100.

Продукт на рынке должен иметь, по крайней мере, 60 единиц очищающих свойств и 60 единиц дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью трех основных очистителей, характеристики которых приводятся ниже:

Сформулируйте задачу нахождения оптимальной смеси как задачу линейного программирования и решите ее.

Задача 1.28. Фирма, выпускающая трикотажные изделия, использует для производства продукции два вида сырья. Все необходимые данные приведены в таблице.

Запишите в математической форме условия выпуска готовой продукции, если сырье расходуется полностью, а прибыль должна быть максимальной.

Задача 1.29. Фабрика производит два основных типа товара. Изделию типа I требуется 3 единицы сырья А и единица сырья В. Оно

приносит прибыль 3 единицы. Изделию типа II требуется 4 единицы сырья А и 3 единицы сырья В. Оно приносит прибыль в 2 единицы. Найдите оптимальный план производства, если доступны всего 20 единиц сырья А и 10 единиц сырья В (используйте графический метод).

Как изменится оптимальный план производства, если окажется доступной еще одна единица сырья А, а затем и еще одна единица сырья В?

Задача 1.30. Рацион кормления коров на молочной ферме может состоять из трех продуктов – сена, силоса и концентратов. Эти продукты содержат питательные вещества – белок, кальций и витамины. Численные данные представлены в таблице. В расчете на одну корову суточные нормы потребления белка и кальция составляют не менее 200 и 210 г соответственно. Потребление витаминов строго дозировано и должно быть равно 87 мг в сутки.

Составьте самый дешевый рацион, если стоимость 1 кг сена, силоса и концентрата равна соответственно 1, 5, 2 и 6 руб.

Раздел 2. ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ

§ 2.1. Составление двойственных задач

Каждой задаче линейного программирования может быть поставлена в соответствие другая вполне определенная задача линейного программирования, такая, что при решении одной из них одновременно решается и другая. Эти задачи были названы парой взаимодвойственных задач.

Исходная задача

§2.2. Правила построения двойственной пары

1.Целевая функция исходной задачи задается на максимум, а целевая функция двойственной – на минимум.

2.Коэффициенты при переменных в системах ограничений описываются матрицами, которые являются транспонированными относительно друг друга.

3.Число переменных в двойственной задаче равно числу соотношений в системе ограничений исходной задачи. Число ограничений

всистеме двойственной задачи равно числу переменных в исходной задаче.

4.Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений другой задачи, и наоборот.

5.Если на j переменную исходной задачи наложено уcловие не-

отрицательности xj 0, то j-е ограничение двойственной задачи яв-

ляется неравенством. Если xj может принимать как положительные,

так и отрицательные значения, то j-е соотношение в системе ограничений двойственной задачи – уравнение.

Аналогично связаны ограничения исходной задачи и переменные двойственной. Если i-е соотношение в системе исходной задачи является неравенством, то i-я переменная двойственной задачи yi 0. В противном случае yi может принимать как положительные, так и отрицательные значения.

§ 2.3. Основные теоремы двойственности

Теорема 2.1 . Если одна из двойственных задач имеет оптимальный план, то и другая также имеет оптимальный план, причем значения целевых функций f и на этих планах равны, т.е. f (X*) (Y*).

Теорема 2.2. Если при подстановке компонент оптимального плана в систему ограничений исходной задачи i-е ограничение обращается в неравенство, то i-я компонента оптимального плана двойственной задачи равна нулю. Если i-я компонента оптимального плана двойственной задачи положительна, то i-е ограничение исходной задачи удовлетворяется ее оптимальным решением как строгое равенство.

§ 2.4. Геометрическая интерпретация двойственных задач

При решении двойственных задач возможны три случая: 1) обе задачи разрешимы;