1055

mx xi 11,95 0,7029;

N 17

my yi 26,83 1,5782;

N 17

D X xi2 mx2 0,0418;

N

D Y 45,41 1,5782 2 0,1806;

17

y 0,4249.

Корреляционный момент равен

Вычисляем коэффициент корреляции:

Используем критерий определения линейной зависимости.

Если rx y N 1 3, то линейная связь между случайными вели-

чинами X,Y достаточно вероятна. В нашем случае получаем, что критерий выполнен: 0,9943 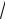17 1 3,97 3, поэтому считаем, что наличие линейной связи между случайными величинами установлено.

Линейная регрессия Y по X имеет вид

ymy rx y y x mx .

x

В нашем случае

y 1,57 0,9943 0,04249 x 0,7029 . 0,2042

Или, после упрощений y 2,0695x 3,0239.

Аналогично x 0,4776y 1,4566 ─ линейная регрессия X по Y .

Заметим, что прямые получаются в результате минимизации суммы квадратов отклонений по вертикали (регрессия Y по X ) или по горизонтали (линейная регрессия X по Y ).

Вопросы для самопроверки

1.Функция распределения двумерных случайных величин. Свойства, формулы для вычисления.

2.Плотность распределения двумерных случайных величин. Свойства, формулы для вычисления.

3.Числовые характеристики двумерных случайных величин.

4.Определение корреляционного момента.

5.Коэффициент корреляции и его свойства.

6.Линейная корреляционная зависимость между случайными величинами. Формулы линейной связи случайных величин.

§ 7.5. Задачи для самостоятельного решения

Установить наличие корреляционной зависимости между различными парами случайных величин из табл. 18.

Окончание табл. 18

Раздел 8. ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ ЗАДАЧИ В АНАЛИЗЕ И ПЛАНИРОВАНИИ ПРОИЗВОДСТВА

§ 8.1. Моделирование экономического процесса

Экономико-математическая модель – это модель, описывающая какой-либо процесс или явление. Математические модели имеют ряд

преимуществ перед другими видами моделей. Например, широкий диапазон применения, довольно низкую стоимость их создания, быстроту получения результатов исследования, возможность экспериментирования с исследуемым экономическим процессом, возможность проверки правильности предпосылок и условий поставленной экономической задачи.

При построении математической модели важно избегать как чрезмерного упрощения экономического явления, так и излишней его детализации и усложнения. Лучшей моделью экономического явления или процесса считается та, которая позволяет получить наиболее рациональное решение. Именно практическая проверка полученных результатов служит окончательным критерием качества созданной модели.

Процесс моделирования экономического явления состоит из трех основных этапов: составление экономико-математической модели, нахождение оптимального решения математическими методами, анализ полученного решения. На первом этапе сначала определяют признак (критерий), по которому будут сравнивать различные варианты решения и выбирать среди них наилучшее, оптимальное решение. В качестве такого критерия могут быть: наибольшая прибыль, наименьшие издержки производства, максимальная загрузка оборудования, наименьшие отходы производства и т.д.

Единого показателя успешной деятельности предприятия не существует. Процесс производства может быть достаточно полно охарактеризован лишь системой экономических показателей. Но при построении математической модели выбирают наиболее важный показатель для данного случая. Этот показатель отражается целевой функцией. Остальные показатели можно включить в систему ограничений, например, в линейном программировании.

n

L x Пj xj max,

j 1

где Пj ─ прибыль, получаемая от производства единицы продукции.

При постановке задач, как правило, предполагается ограниченность ресурсов, которые необходимо оптимально распределить на производство продукции. Если все виды ресурсов, к которым относятся запасы сырья, трудовые ресурсы, мощность оборудования и т.д., используются на выпуск продукции, то получаем ограничение моде-

n

ли: aijxj Wi , где aij ─ норма расхода i-го вида сырья на произ-

j 1

водство j-го вида продукции; Wi ─ запасы i-го вида ресурса. Условия выполнения договорных поставок запишем неравенст-

вом di xi Di , i n, где di и Di ─ нижняя и верхняя границы производства продукции i-го вида.

Продукцию нельзя превращать в сырье. Это условие записывается неравенством xj 0, j 1,2,...,n.

Все уравнения, отражающие экономический процесс, должны быть непротиворечивыми, то есть должно существовать хотя бы одно решение задачи, удовлетворяющее всем ограничениям.

Не для всякой экономической задачи требуется создавать собственную математическую модель. Существуют типовые модели, к которым приводятся множество конкретных задач. Математическая модель, отражающая однотипные экономические процессы, называется фундаментальной экономической моделью. В экономическом анализе, в планировании и управлении производством на предприятии, производственными силами в территориальных экономических системах, в экономике страны используются около 100 фундаментальных экономико-математических, информационных моделей.

§ 8.2. Фундаментальная модель диеты

i-го элемента в единице веса j-го компонента; bi ─ количество, стандарт i-го элемента в диете (смеси).

Целевая функция (19) показывает необходимость составления смеси при минимальной стоимости. Уравнение (20) характеризует выполнение стандарта i-го элемента в диете (смеси). Неравенство

(21) показывает условие неотрицательности, то есть превращение диеты (смеси) обратно в компоненты невозможно.

Модель (19)─(21) используется при составлении рецептур мороженого, плавленых сыров, кремов пищевой промышленности, а при замене (20) – для смесок в текстильной промышленности при оптимальном раскрое материала, в легкой и других отраслях производства.

Пример. Составление рецептуры мороженого. В методах расчета рецептуры мороженого учитываются только технологические условия и не учитываются экономические ограничения. Однако от выбранного рецепта, то есть от количества и вида сырья, расходуемого на единицу продукции, зависит себестоимость смеси, от которой, в свою очередь, зависит себестоимость выпускаемой продукции и рентабельность предприятий по производству мороженого.

Экономико-математический метод расчета рецептуры смеси мороженого позволяет составлять смесь при минимальной себестоимости выпускаемой продукции с учетом всех технологических условий. Он применим для составления смеси сливочного, пломбирного, молочного и прочих видов мороженого. Расчет рецептуры этих видов мороженого сводится к решению задачи линейного программирования, представленной следующей экономико-математической моделью.

Требуется составить смесь мороженого, имеющего минимальную себестоимость

при выполнении таких технологических условий:

где xj ─ количество единиц j-го продукта, вводимого в смесь; ai j

─ коэффициенты матрицы, обозначающей содержание элемента i в единице j-го продукта (сырья); cj - оптовая цена единицы j-го про-

дукта (сырья); n ─ количество исходных видов сырья, возможных для применения при составлении смеси; N ─ допустимая норма введения в смесь группы компонентов.

j 1

Условие, показывающее, что сумма мощностей поставщиков равна спросу всех пунктов потребления, записывается уравнением

Оптимальный вариант плана поставок, характеризующийся минимальным грузооборотом, можно записать в виде целевой функции вида

i 1 j 1

Мощности пунктов отправления и спросов потребителей должны быть неотрицательными:

Обратные перевозки от потребителей к поставщикам исключаются, то есть

Экономико-математическая модель транспортной задачи, описываемая условиями (22) – (27), называется закрытой.

Если сумма мощностей поставщиков не равна сумме мощностей потребителей, то вместо условия (24) используем условия

а вместо условия (23) используем условие

j 1

Модель транспортной задачи, имеющей условие (28), называется открытой.

При планировании перевозок часто приходится учитывать ограничительные пропускные способности перевозок. Эти ограничения записываются в виде неравенств

где i j ─ предельное число единиц продукта, перевозимое по ком-

муникациям Ai Bj , за время, оговоренное в условиях задачи.

Существуют и другие модификации модели транспортной задачи, которые можно свести к классической постановке различными преобразованиями.

Пример. Оптимальное размещение предприятий. В общем виде задачу развития и размещения предприятий любой отрасли промышленности в стране, регионе, решаемую по критерию минимума затрат, можно сформулировать следующим образом: при фиксированной потребности в продукции отрасли в плановой перспективе, дифференцированной по пунктам потребления, при известном состоянии отрасли в начале периода, при заданной сырьевой базе и транспортной сети определить, какой вариант строительства новых предприятий (место строительства, мощность предприятия и их специализация) и реконструкции действующих предприятий сведет совокупные затраты к минимуму.

Как правило, наилучший результат решения получается с учетом двух основных факторов: экономии на производственных издержках при увеличении мощности предприятия и возможного проигрыша при этом из-за увеличивающихся транспортных затрат. Определение наилучшего сочетания этих факторов при равных остальных условиях позволит найти наиболее выгодный вариант размещения предприятий отрасли. Поэтому оба фактора должны иметь четкие количественные выражения.

При использовании закрытой модели такого рода задач возникает жесткая балансировка спроса и предложения в ограничениях задачи. В результате в закрытой модели можно учесть только один фактор, например, транспортный, и мы находим только оптимальную схему перевозок. При открытой модели возможен выбор поставщиков с наиболее низкими затратами, меняется схема прикрепления поставщиков к потребителям продукции. Таким образом, возникает возможность одновременного учета действия производственного и транспортного факторов. Модель имеет цель: найти вариант размещения предприятий, позволяющий получить минимум затрат на производство и доставку продукции потребителям. Это условие записывается в виде целевой функции

i 1

где xi j ─ величины поставок от i-го поставщика к j-му потребите-

лю; xi ─ мощность предприятия в i-м пункте; ci j ─ затраты на произ-

водство и доставку единицы продукции от i-го поставщика к j-му потребителю; ai ─ мощность действующих предприятий, стоимость реконструкции или нового строительства; bj ─ потребность в продук-

те j-го пункта потребления.

Оптимальный вариант решения задачи (31)─(34) показывает транспортные связи и варианты размещения производства. При таком подходе к решению задачи оптимального размещения промышленного производства постановка задачи проста, сравнительно несложно получение исходной информации для построения модели, вычислительные алгоритмы надежны.

Модель (31)─(34) используется для решения задач развития и размещения различных отраслей промышленности. Наиболее удачные решения были получены в размещении предприятий птицеперерабатывающей, сыродельной, маслодельной, пищевой, легкой, текстильной промышленности и предприятий услуг. Однако данная модель не учитывает многих факторов, поэтому решение задачи дает самое общее представлении о характере размещения предприятий. Модель (31)─(34) желательно использовать на предварительных этапах исследования.

Недостатки рассмотренной модели появляются из-за того, что мы предполагаем линейным характер зависимости затрат на производство и объема производства. В реальности данная зависимость нелинейна. Увеличение затрат на производство ведет к снижению удельных текущих затрат из-за постоянства целого ряда статей затрат или, по крайней мере, в результате более медленного их роста. В итоге получаем гиперболическую зависимость себестоимости и объема производства.

Целевая функция имеет нелинейный вид: