Математическая статистика.
По данному распределению выборки построить эмпирическую функцию распределения, гистограмму и полигон:
|
xi |
1 |
2 |
3 |
4 |
5 |
6 |
|
ni |
20 |
10 |
35 |
5 |
10 |
20 |
Найти точечную оценку параметра pбиномиального распределения (схема Бернулли) по выборке (1,1,0,0,1,0,0,1,0,1,0,1), где Х
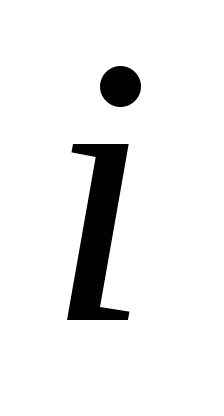принимает
значения: 1 с вероятностью р и 0 с
вероятностью 1-р: а) методом моментов и
б) методом максимального правдоподобия.Найти доверительный интервал надежности 1-α=0,9 для неизвестного математического ожидания при неизвестной дисперсии по выборке:
|
№ |
1 |
2 |
3 |
4 |
5 |
|
X |
4,781 |
4,795 |
4,769 |
4,792 |
4,779 |
Распределение нормальное. Какова точность этого интервала? Как изменится точность, если дисперсия известна и равна 0,0004?
Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза об экспоненциальном распределении генеральной совокупности с результатами наблюдений, представленными в таблице:
|
интервалы |
0- 0,2 |
0,2-0,4 |
0,4-0,6 |
0,6-1,4 |
1,4-1,6 |
1,6-2,0 |
2,0-3,0 |
3,0-4,0 |
4,0-6,0 |
6,0-8,0 |
|
n |
14 |
22 |
30 |
20 |
18 |
20 |
24 |
28 |
16 |
8 |
