22. Гипербола.

Геометрическое место точек, модуль разности расстояний от которых до двух фиксированных точек плоскости постоянна, называется гиперболой.

Каноническое уравнение гиперболы: , где .

Гипербола есть линия второго порядка.

Гипербола имеет 2 асимптоты: и

Гипербола называется равносторонней, если ее полуоси равны. (а=b). Каноническое уравнение:

Эксцентриситет – отношение расстояния между фокусами к величине действительной оси гиперболы:

Так как для гиперболы с>а , то эксцентриситет гиперболы >1.

Эксцентриситет характеризует форму гиперболы: . Эксцентриситет равносторонней гиперболы равен равен .

Директрисы – прямые .

Фокальные радиусы: и .

Есть гиперболы, которые имеют общие асимптоты. Такие гиперболы называются сопряженными.

23. Парабола.

Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Расстояние от фокуса до директрисы – параметр параболы (p>0).-полуфокальный диаметр.

Парабола есть линия второго порядка.

М(х,у) – произвольная точка параболы. Соединим точку М с F, проведем отрезок MN перпендикулярно директрисе. Согласно определению параболы MF=MN. По формуле расстояния между 2 точкам находим: => = =>

=>

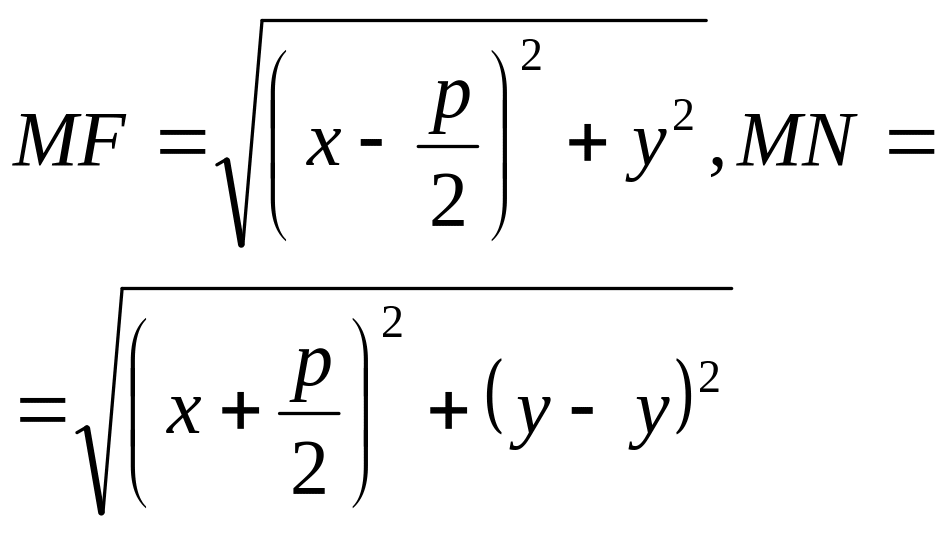Каноническое уравнение параболы: y² = 2px.

24. Эллипсоид.

Исследуем поверхность, заданную уравнением:

Рассмотрим сечения поверхности с плоскостями, параллельными плоскости xOy. Уравнения таких плоскостей: z=h,где h – любое число. Линия, получаемая в сечении, определяется двумя ур-ниями:

z=h .

Исследуем поверхность:

А) если то Линия пересечения поверхности с плоскостями z=h не существует.

Б) если , линия пересечения вырождается в две точки (0,0,с), и (0,0,-с). Плоскости z = c, z = - c касается данной поверхности.

В) если , то уравнения можно переписать в виде: 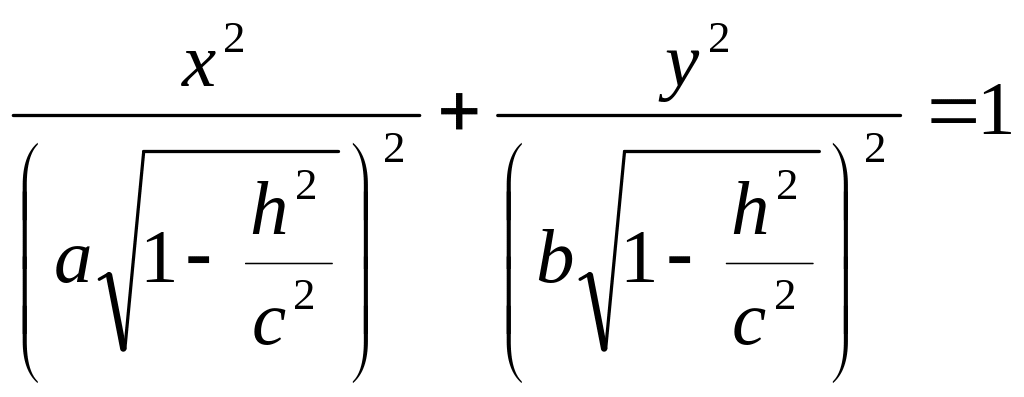, как видно, линия пересечения есть эллипс с полуосями а1 = , b1 = . При этом, чем меньше h, тем больше полуоси. При н=0 они достигают своих наибольших значений. а1=а, b1=b. Уравнения примут вид:

h=0.

Рассмотренные сечения позволяют изобразить поверхность как замкнутую овальную поверхность. Поверхность называется эллипсоидами., если какие-либо полуоси равны, трехосный эллипсоид превращается в эллипсоид вращения, а если а=b=c, то в сферу.