
7. Тригонометрия
.doc
§7.
ТРИГОНОМЕТРИЯ
Соотношения
между тригонометрическими функциями
одного
и того же аргумента .
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Формулы приведения
Формулы
приведения применяются по следующей
схеме:
1) если под знаком преобразуемой
тригонометрической функции содержится
сумма аргументов вида
![]() то
наименование тригоно-метрической
функции следует сохранить;
2) если
под знаком преобразуемой тригонометрической
функции содержится сумма аргументов
вида
то
наименование тригоно-метрической
функции следует сохранить;
2) если
под знаком преобразуемой тригонометрической
функции содержится сумма аргументов
вида
![]() то
наименование тригоно-метрической
функции следует изменить:
то
наименование тригоно-метрической
функции следует изменить:
![]() ,
,
![]() ;
3) перед полученной функцией от
аргумента
;
3) перед полученной функцией от
аргумента
![]() надо
поставить тот знак, которая имела
бы
преобразуемая функция при условии, что
надо
поставить тот знак, которая имела
бы
преобразуемая функция при условии, что
![]() .
.
Функции
суммы и разности двух углов
![]() ,
,![]() ;
;
![]() .
.
Функции
двойного аргумента
![]() ,
,
![]() ,
,
57
![]() ,
,
![]() .
.
Формулы
понижения степени
![]() ,
,
![]() .
.
Функции
половинного аргумента
![]() ,
,
![]() .
.
Формулы
преобразования суммы функций в
произведение:
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
Формулы
преобразования произведения в сумму
![]() ,
,
![]() ,
,
![]() .
.
58
Формула
дополнительного аргумента
![]() ,
где
,
где
![]() .
.
Периодичность;
четность и нечетность
![]() ,
,
![]() ,
,
![]() (нечетная);
(нечетная);
![]() ,
,
![]() ,
,
![]() (четная
;
(четная
;
![]() ,
,
![]() ,
,
![]() (нечетная);
(нечетная);
![]() ,
,
![]() ,
,
![]() (нечетная).
(нечетная).
Обратные
тригонометрические функции
![]() ,
где
,
где
![]() ,
если
,
если
![]() и
и
![]() :
:
![]() ,
где
,
если
,
где
,
если
![]() и
и
![]() ;
;
![]() ,
где
,
где
![]() ,
если
,
если
![]() и
и
![]() ;
;
![]() ,
где
,
если
,
где
,
если
![]() и
и
![]() .
Имеют место следующие соотношения
между обрат-ными тригонометрическими
функциями, справедливые в области
определения соответствующих
функций:
.
Имеют место следующие соотношения
между обрат-ными тригонометрическими
функциями, справедливые в области
определения соответствующих
функций:
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
59
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Решение
простейших тригонометрических
уравнений:
.
Решение
простейших тригонометрических
уравнений:
![]() ––
––
![]() ;
;
![]() ––
––
![]() ;
;
![]() ––
––
![]() ;
;
![]() ––
––
![]() .
.
Пример
1. Вычислить
![]() .
.
Решение.
Так как
![]()
![]() то
то
![]() .
.
Ответ:
0.
Пример 2.
Вычислить
![]() .
.
Решение.
Воспользуемся формулой синуса двойного
аргу-мента и формулой приведения
![]() :
:
60
![]()
![]() .
.
Ответ:
0,125
Пример 3.
Вычислить
![]() .
Решение.
Воспользуемся периодичностью функции
.
Решение.
Воспользуемся периодичностью функции
![]() и
формулой
и
формулой
![]() :
:
![]() .
Поэтому
.
Поэтому
![]() .
Ответ:
– 0,1.
.
Ответ:
– 0,1.
Пример
4. Вычислить
![]() .
Решение.
Применяя формулу приведения, получим
.
Решение.
Применяя формулу приведения, получим
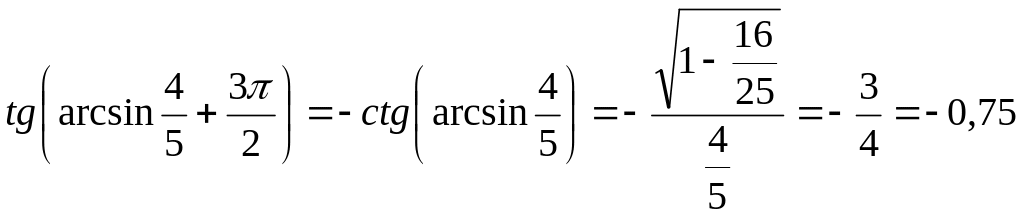 .
Ответ:
–0,75.
.
Ответ:
–0,75.
Пример
5. Вычислить
![]() .
Решение.
Учитывая, что
.
Решение.
Учитывая, что
![]() и
и
61
![]() ,
получим
,
получим
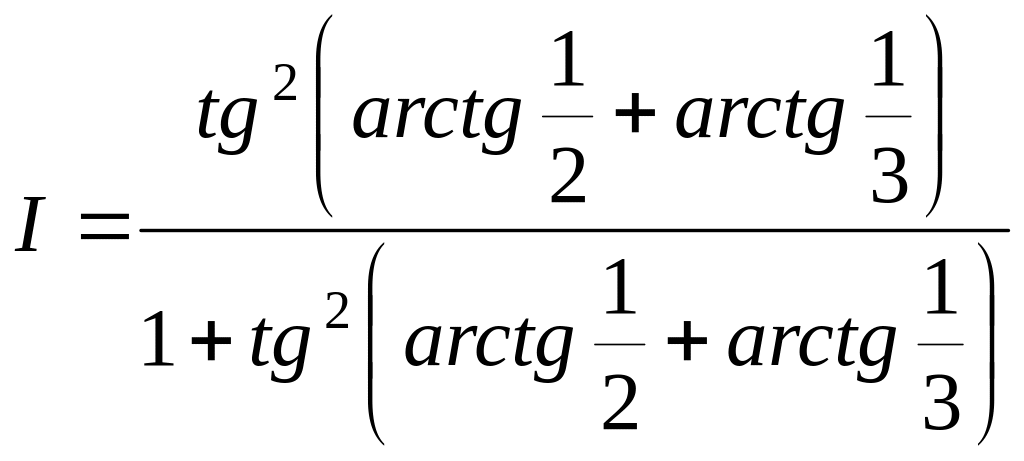 .
Применим формулу тангенса суммы:
.
Применим формулу тангенса суммы:
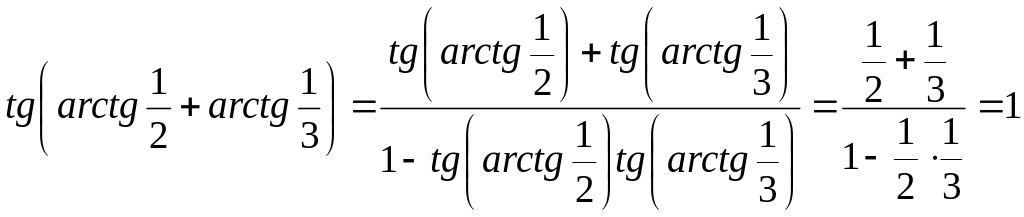 .
Следовательно,
.
Следовательно,
![]() .
.
Ответ: 0,5.
Пример
6. Вычислить
![]() ,
если
,
если
![]() .
.
Решение.
Так как
![]() и
и
![]() ,
то
,
то
![]() .
.
Ответ: 0,3.
Пример
7. Вычислить
![]() при
при
![]() .
Решение.
.
Решение.
![]()
![]()
62
![]()
![]() .
Ответ:
– 0,5.
Пример
8. Найти в
градусах корень уравнения
.
Ответ:
– 0,5.
Пример
8. Найти в
градусах корень уравнения
![]() ,
если
,
если
![]() Решение.
Так как
Решение.
Так как
![]() ,
то исходное урав-нение можно записать
в виде
,
то исходное урав-нение можно записать
в виде
![]() ,
или
,
или
![]() .
.
Обозначив
![]() ,
получим:
,
получим:
![]() .
Корни это-го уравнения:
.
Корни это-го уравнения:
![]() .
Вернемся к переменной х:
.
Вернемся к переменной х:
1)
![]() .
Это уравнение решений не имеет.
.
Это уравнение решений не имеет.
2)
![]() .
Корень этого уравнения, лежащий в
интервале
.
Корень этого уравнения, лежащий в
интервале
![]() ,
равен
,
равен
![]() Ответ
:
Ответ
:
![]() .
Пример 9.
Найти сумму
корней уравнения
.
Пример 9.
Найти сумму
корней уравнения
![]() ,
если
,
если
![]() .
Решение.
Так как
.
Решение.
Так как
![]() ,
,
то исходное уравнение равносильно уравнению
![]()
![]()
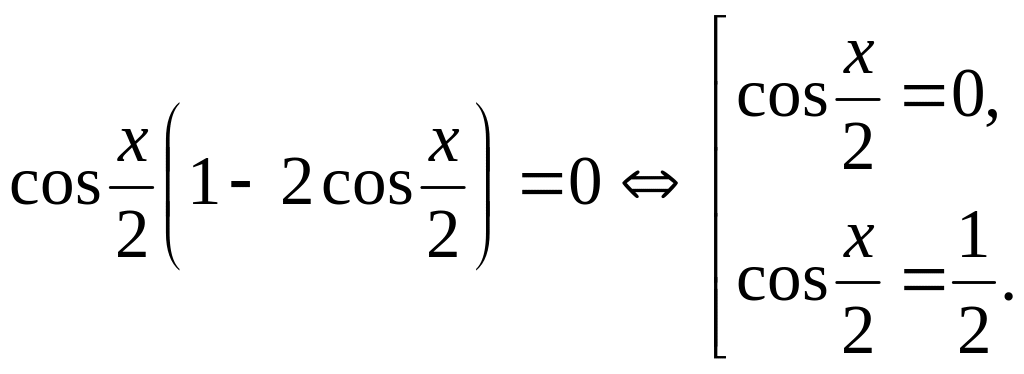
а)
![]() ;
;
![]() ,
т.е.
,
т.е.
![]() ,
,
![]()
63
При
![]() получаем решение
получаем решение
![]() из
заданного интерва-ла
из
заданного интерва-ла
![]() .
При остальных значениях
.
При остальных значениях
![]() соответствующие значения
соответствующие значения
![]() не принадлежат промежутку
.
не принадлежат промежутку
.
б)
![]() ;
;
![]() ;
;
![]() ,
,
![]()
В интервале
![]() лежит только одно решение
лежит только одно решение
![]() заданного уравнения.
заданного уравнения.
![]() .
.
Ответ :
![]() .
.
Пример 10. Сколько
корней имеет уравнение
![]() в промежутке
в промежутке
![]() ?
Решение.
Умножим обе части уравнения на
?
Решение.
Умножим обе части уравнения на
![]() :
:
![]() .
Отсюда
.
Отсюда
![]() ;
;
![]() ,
,
![]() .
.
![]() ;
;
![]() .
При других значениях
соответствующие
значения
не принадле-
жат заданному отрезку.
.
При других значениях
соответствующие
значения
не принадле-
жат заданному отрезку.
Ответ:
2.
Пример 11.
Сколько корней имеет уравнение
![]() в промежутке
в промежутке
![]() ?
Решение.
Так как
?
Решение.
Так как
![]() ,
то данное уравнение можно записать в
виде
,
то данное уравнение можно записать в
виде
![]() .
(1)
.
(1)
64
![]()
![]()
![]() Решим
уравнение
Решим
уравнение
![]() .
Обозначив
.
Обозначив
![]() ,
получим
,
получим
![]() .
Корни этого уравне-ния:
.
Корни этого уравне-ния:
![]() .
Вернемся к переменной
.
а)
.
Вернемся к переменной
.
а)
![]() .
Это уравнение решений не имеет.
б)
.
Это уравнение решений не имеет.
б)
![]() .
.
![]() .
Рассмотрим
эти две серии значений
отдельно.
1)
.
Рассмотрим
эти две серии значений
отдельно.
1)
![]() (3)
(3)
![]() .
Так как
.
Так как
![]() и
и
![]() ,
то
,
то
![]() – решение системы (2).
– решение системы (2).
![]() .
Это значение
не является ре-
шением системы (2),
так как
.
Это значение
не является ре-
шением системы (2),
так как
![]() .
.
65
При
остальных значениях
соответствующие значения
из (3) не принадлежат заданному интервалу.
2)
![]() .
(4)
.
(4)
![]() .
Так
как
.
Так
как
![]() и
и
![]() ,
то
,
то
![]() – решение системы (2).
– решение системы (2).
![]() .
Это значение
не является решением системы (2), так как
.
Это значение
не является решением системы (2), так как
![]() .
При
остальных значениях
соответствующие значения
из (4) не принадлежат заданному интервалу.
Итак, исходное уравнение в интервале
.
При
остальных значениях
соответствующие значения
из (4) не принадлежат заданному интервалу.
Итак, исходное уравнение в интервале
![]() имеет два
решения:
имеет два
решения:
![]() .
.
Ответ:
![]() .
Пример 12. Решить
неравенство
.
Пример 12. Решить
неравенство
![]()
Решение.
Перепишем исходное неравенство в
следующем виде:
![]() .
(5)
Так как
.
(5)
Так как
![]() при всех
при всех
![]() ,
то неравенство (5) равно-сильно неравенству
,
то неравенство (5) равно-сильно неравенству
![]() ,
т.е.
,
т.е.
![]() .
Прямая
.
Прямая
![]() пересекает числовую окружность в точках
пересекает числовую окружность в точках
![]()
66
и
![]() .
Неравенству
.
Неравенству
![]() соответствуют точки открытой дуги
соответствуют точки открытой дуги
![]() .
Дуга
– это дуга с началом в точке
и кон-цом в точке
при движении по окружности против
часовой стрелки.
.
Дуга
– это дуга с началом в точке
и кон-цом в точке
при движении по окружности против
часовой стрелки.

Точка
соответствует числу
![]() ,
а точка
– числу
,
а точка
– числу
![]() .
Итак, решения неравенства
,
принадлежащие
.
Итак, решения неравенства
,
принадлежащие
промежутку
![]() длиной
длиной
![]() ,
таковы:
,
таковы:
![]() .
.
Вследствие
периодичности косинуса остальные
решения получаются прибавлением к
найденным чисел
![]() ,
где
,
где
![]() .
.
Приходим
к ответу:
![]() ,
.
,
.
Ответ: , .
67
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Упростить выражение:
а)
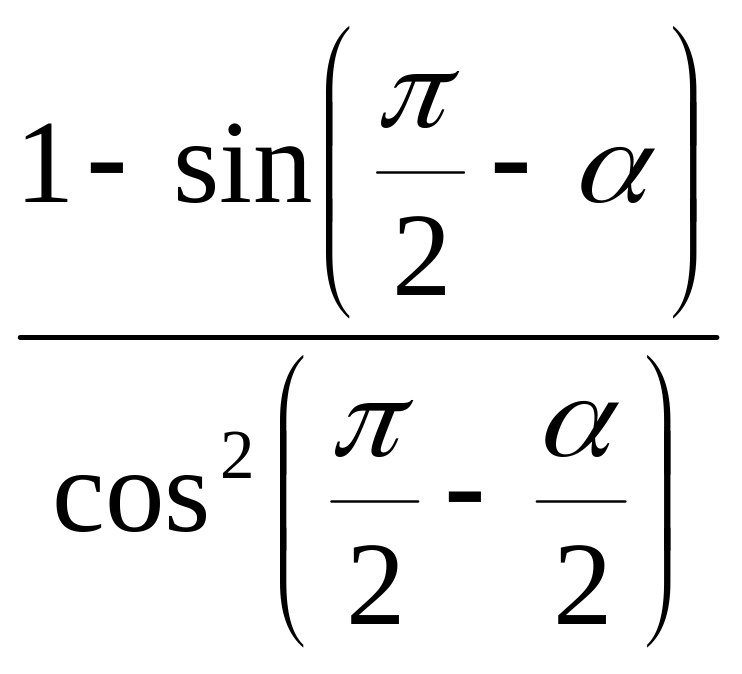 ;
(Ответ:
2)
;
(Ответ:
2)
б)
![]() ;
(Ответ:
0,75)
;
(Ответ:
0,75)
в)
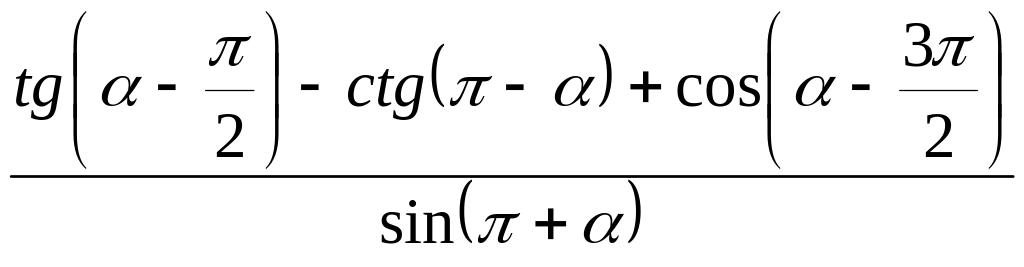 ;
(Ответ:
1)
;
(Ответ:
1)
г)
![]() .
(Ответ:
1)
.
(Ответ:
1)
2. Вычислить:
а)
![]() ;
(Ответ:
3)
;
(Ответ:
3)
б)
![]() ;
(Ответ:
1)
;
(Ответ:
1)
в)
![]() ;
(Ответ:
– 2)
;
(Ответ:
– 2)
г)
![]() ;
(Ответ:
4)
;
(Ответ:
4)
д)
![]() ;
(Ответ:
4,5)
;
(Ответ:
4,5)
е)![]() ;
(Ответ:
– 0,2)
;
(Ответ:
– 0,2)
ж)
![]() .
(Ответ:
0,48)
.
(Ответ:
0,48)
68
3. Найти значение выражения:
а)
![]() ,
если
,
если
![]() ;
(Ответ:
7)
;
(Ответ:
7)
б)
![]() ,
если
,
если
![]() ;
(Ответ:
;
(Ответ:
![]() )
)
в)
![]() ,
если
,
если
![]() и
и
![]() .
.
(Ответ:
![]() )
)
4. Сколько корней имеет уравнение
![]() при
при
![]() ?
?
(Ответ: 3)
5.
Сколько корней имеет уравнение
![]()
при
![]() ?
(Ответ:
1)
6.
Найти
в градусах корень уравнения
?
(Ответ:
1)
6.
Найти
в градусах корень уравнения
![]() ,
если
,
если
![]() .
(Ответ:
180)
7.
Найти в градусах наименьший положительный
корень урав-
нения
.
(Ответ:
180)
7.
Найти в градусах наименьший положительный
корень урав-
нения
![]() .
(Ответ:
30)
8. Найти
в градусах корень уравнения
.
(Ответ:
30)
8. Найти
в градусах корень уравнения
![]() ,
если
,
если
