§5. Показательные уравнения и
Неравенства. Логарифмы.
Логарифмические уравнения и
Неравенства
Показательная функция:
,
где
.
Свойства показательной функции
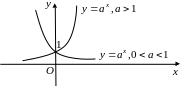1. Область
определения:
.
2. Область значений:
.
3. При
функция
монотонно возрастает, а при
– монотонно убывает.
4. График
функции
имеет вид
Логарифмом числа
по
основанию
,
называется
число
,
для которого
.
.
Основные свойства логарифмов
1.
2.
.
3. Основное логарифмическое тождество:
,
.
4.
.
38
5.
.
6.
.
7.
8.
,
.
Логарифмическая
функция:
Свойства логарифмической
функции
1. Область определения: . 2. Область значений: . 3. При функция монотонно возрастает, а при – монотонно убывает. 4. График функции имеет вид
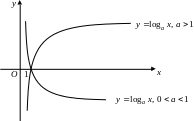
Показательные уравнения Решение показательных уравнений основано на свойстве степеней: две степени с одним и тем же положительным и отличным от единицы основанием равны тогда и только
39
тогда, когда равны их показатели.
1.
.
2.
3.
.
4.
Уравнение вида
,
где
,
,
,
с помощью подстановки
сводится к квадратному уравнению
.
Логарифмические уравнения
1.
Уравнение
,
где
,
равносильно
уравнению
.
2.
3.
Решение простейших показательных и логарифмических неравенств основано на свойствах монотонности показа- тельной и логарифмической функций:
при
:
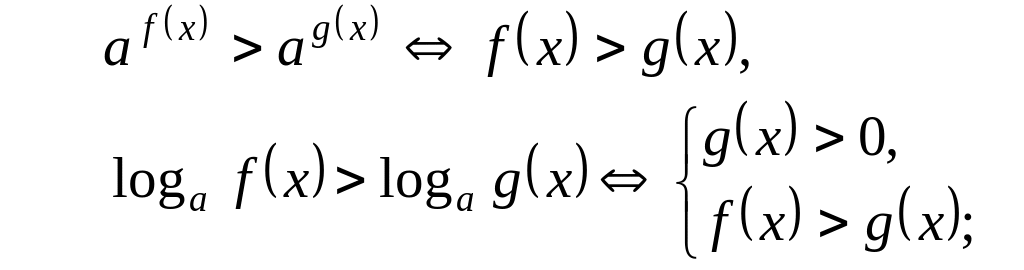
40
при :
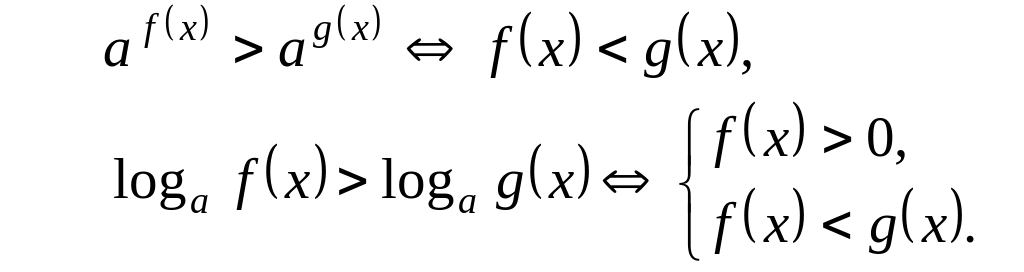
Пример 1. Решить
уравнение:
.
Решение. Так
как
и
,
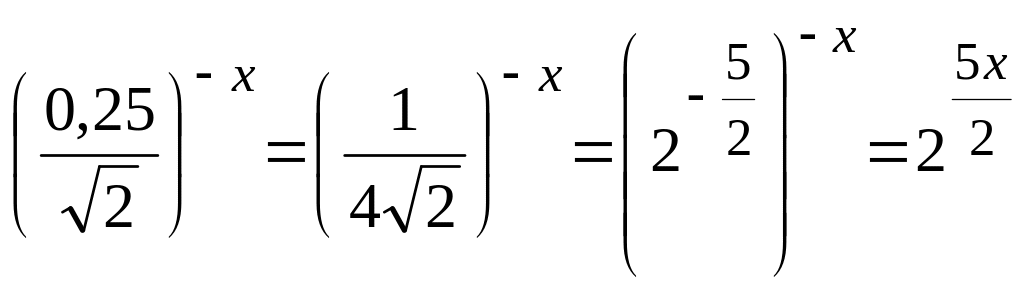то исходное уравнение равносильно
уравнению
,
откуда
Ответ:
.
Пример
2. Решить уравнение:
.
Решение.
Ответ:
.
Пример 3. Решить уравнение:
.
Решение.
Разделив обе части исходного уравнения
на
(
при всех
),
получим равносильное ему уравнение :
;
.
41
Обозначив
,
,
последнее уравнение запишем в виде
.
Корнями
этого уравнения являются
и
.
Учитывая, что
положительное
число, получим:
.
Тогда:
;
.
Ответ:
.
Пример 4.
Вычислить
.
Решение.
,
.
Поэтому
.
Ответ: 1125.
Пример 5.
Вычислить
.
Решение.
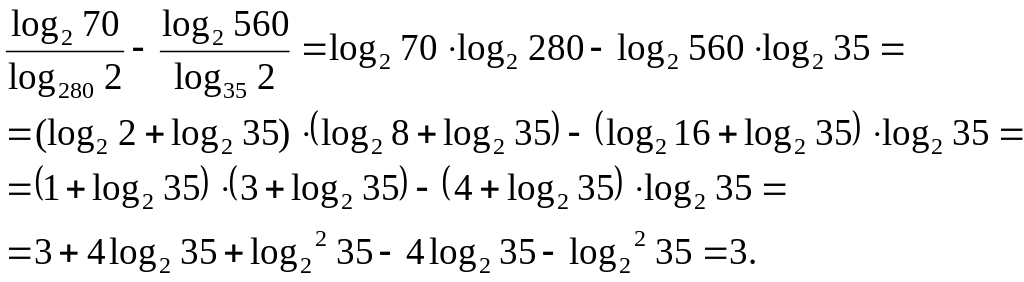Ответ:
3.
Пример 6.
Вычислить
.
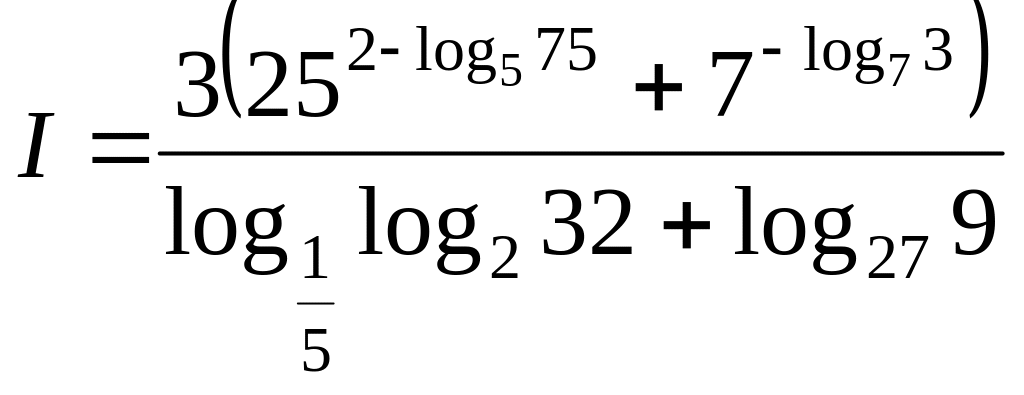42
Решение.
;
.
Следовательно,
.
Ответ: – 4.
Пример 7. Решить
уравнение:
Решение. Так как
,
то исходное уравнение можно записать
в виде:
.
(1)
ОДЗ уравнения
(1) :
т. е.
(2)
На
ОДЗ (2) уравнение (1) равносильно уравнению
Корнями последнего уравнения являются
и
,
из которых
входит в ОДЗ (2), а
нет.
Поэтому единственным корнем исходного
уравнения является число 2.
Ответ
:
.
43
Пример
8. Решить
уравнение:
.
(3)
Решение.
ОДЗ уравнения (3):
.
Обозначим
.
Тогда
и
уравнение (3) принимает вид:
.
Корни
последнего уравнения:
и
.
Так как
,
то
.
Ответ:
.
Пример 9. Найти
сумму корней уравнения:
.
Решение. ОДЗ
уравнения:
.
Прологарифмируем обе части данного
уравнения по основанию 10 :
;
,
т.е.
.
Обозначив
,
получим квадратное уравнение
,
корни которого –
.
.
.
Ответ: 110.
Пример 10. Найти наименьшее целое
значение
,
удовлет-
воряющее неравенству
.
Решение. Поскольку
,
то данное не-
равенство равносильно
неравенству
,
получим
.
Вернемся
к переменной
:
,
откуда
44
.
Наименьшее целое значение
из этого интерва-ла равно
.
Ответ:
.
Пример 11.
Найти число целых решений неравенства
.
Решение.
Поскольку
,
,
то данное неравенство равносильно
неравенству
.
Полученный интервал содержит целые
числа
.
Ответ: 4.
Пример
12. Найти
длину интервала решений неравенства:
.
(4)
Решение.
ОДЗ
неравенства (4):
.
(5)
На ОДЗ неравенство (4) равносильно
неравенству
.
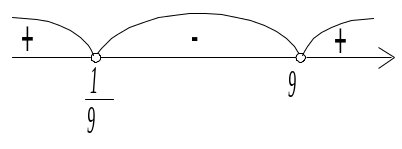
Решая последнее неравенство методом
интервалов и учитывая ОДЗ (5) , получим,
что решением не-
равенства
(4) является интервал
.
Длина этого интер-
вала:
.
Ответ: .
45
Пример
13. Найти
длину интервала решений неравенства
.
Решение.
ОДЗ неравенства:
.
Так как
,
то
исходное неравенство можно записать в виде
,
откуда
.
Длина этого интервала:
.
Ответ:
.
Пример 14. Найти область определения функции
.
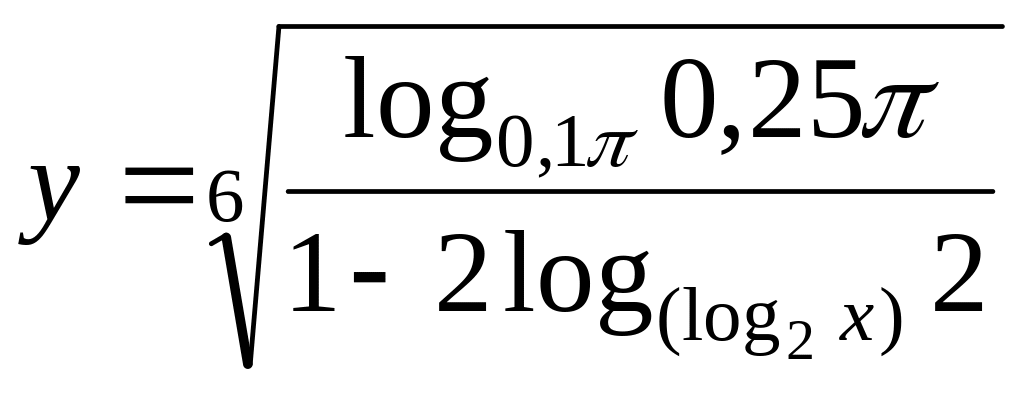Решение. Так
как
,
то область определения данной функции
состоит из
,
удовлетворяющих системе:
.
Ответ:
46
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решить уравнение:
а)
;
(Ответ: 10)
б)
;
(Ответ: 1)
в)
;
(Ответ: 5)
г)
;
(Ответ: 1)
д)
;
(Ответ: 1,5)
е)
;
(Ответ: 2)
ж)
(Ответ:
)
2.
Найти больший корень уравнения:
а)
;
(Ответ:
6)
б)
.
(Ответ: 3)
3. Найти наибольшее целое значение , удовлетворяющее не-
равенству:
а)
;
(Ответ:
3)
б)
.
(Ответ:
–2)
4. Найти наименьшее целое значение , удовлетворяющее
неравенству
а)
;
(Ответ: 2)
б)
;
(Ответ: –
2)
47
в)
.
(Ответ: 3)
5.
Найти число целых решений неравенства
.
(Ответ: 8)
6.
Вычислить:
а)
;
(Ответ: – 40)
б)
;
(Ответ: 19)
в)
;
(Ответ: 13)
г)
;
(Ответ: 1)
д)
;
(Ответ: 1)
е)
.
(Ответ: 4)
7.
Решить уравнение:
а)
;
(Ответ: 3)
б)
;
(Ответ: 1)
в)
;
(Ответ: 50)
г)
;
(Ответ:
)
д)
.
(Ответ: 4)
48
8. Найти сумму корней уравнения:
.
(Ответ: 84)
9.
Найти больший корень уравнения:
а)
;
(Ответ:
625)
б)
.
(Ответ:
64)
10. Найти наименьшее целое значение , удовлетворяющее
неравенству:
а)
;
(Ответ: 4)
б)
.
(Ответ: 2)
11.
Найти сумму целых решений неравенства:
а)
;
(Ответ: 6)
б)
;
(Ответ: 3)
в)
;
(Ответ: –1)
г)
.
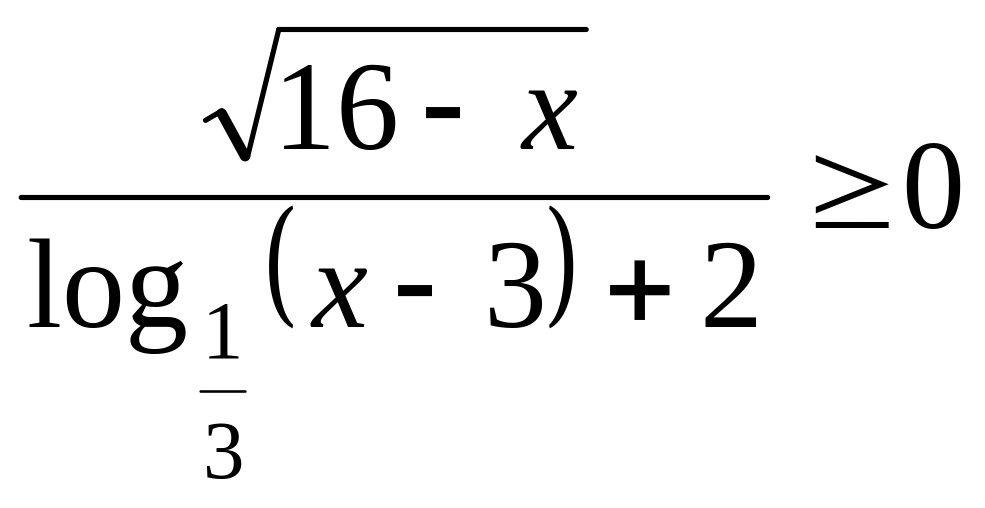(Ответ:
76)
12. Найти наименьшее целое значение из области определения функции
.
(Ответ: 512)
13.
Найти число целых значений
,
принадлежащих области определения
функции
.
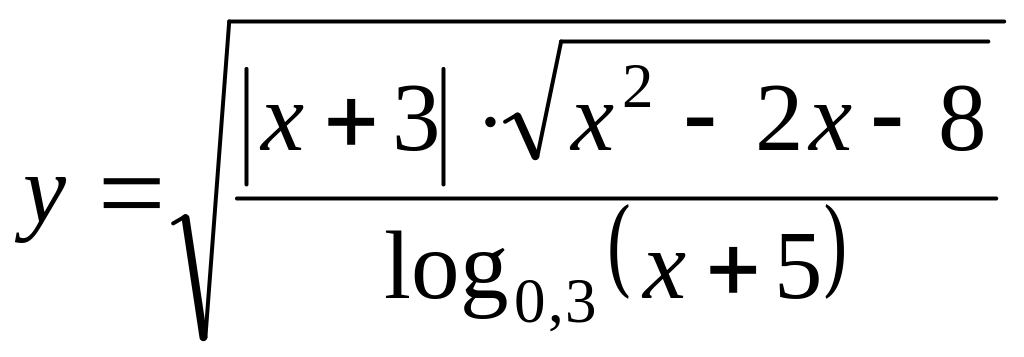(Ответ: 3)
49
14.
Найти длину интервала решений неравенства:
а)
;
(Ответ:
3,25)
б)
.
(Ответ: 1,5)
15.
Решить неравенство:
.
(Ответ:
)
16. Найти наименьшее целое решение неравенства:
.
(Ответ: 3)
50