8. Текстовые задачи

§8. ТЕКСТОВЫЕ ЗАДАЧИ Текстовые задачи классифицируют по следующим типам: задачи “на проценты”; задачи “на работу”; задачи “на дви- жение”; задачи “на смеси” и “ на сплавы”. Эти задачи обычно решают по следующей схеме: выбирают неизвестные; записывают связи между известными и неизвестными величинами в виде уравнений или неравенств, откуда и находят искомые величины. Ниже на ряде примеров показано, как это делается. Задачи “на проценты” Процентом данного числа называется его сотая часть: 1 % от числа равен . Следует помнить, что выражение показывает: сколько процентов от числа составляет число . Пример 1. После двух последовательных повышений зарплата увеличилась в раза. На сколько процентов повысилась зарплата в первый раз, если второе повышение по коли- честву процентов было вдвое больше, чем первое ? Решение. Пусть первоначальная зарплата была равна руб. После первого повышения на % она составила руб.; после второго повышения на % она составила: , т.е. руб. Поэтому, , откуда получаем: ; . Ответ: 25.

71

Пример 2. Цена товара снижена на 40 %, а зарплата дваж-ды увеличивалась на 20 %. На сколько процентов больше

можно купить товара после снижения цен и повышения зарплаты? Решение. Пусть первоначальная зарплата – руб., а руб. – цена условной единицы товара. Количество куплен- ного товара составит условных единиц. После снижения цен условная единица товара стоит руб. Зарплата после пер- вого повышения составит руб., а после второго повышения – руб. Тогда количество товара, которое можно купить на эти деньги, равно , что составляет от перво- начального.

Ответ: . Пример 3. Длину кирпича увеличили на 25 %, ширину на 30 %, а высоту уменьшили на 40 %. На сколько процентов уменьшился объем кирпича ?

Решение. Пусть первоначальные длина, ширина и высота кирпича были равны, соответственно, , , . Тогда  первоначальный объем кирпича. Объем кирпича после изменения его размеров :

.

.

Ответ: .

Задачи “на движение” Пример 4. Поезд прошёл 1/4 расстояния АВ, равного 240 км, и был задержан на 36 минут. Затем он увеличил скорость на 10 км/ч и пришёл в пункт В по расписанию. Найти первоначальную скорость поезда (км/ч ).

72

Решение. Пусть км/ч – первоначальная скорость поезда. Задержку в 36 минут ( 3/5 часа) поезд ликвидировал на расстоянии км, проезжая со скорость км/ч. Следовательно, , откуда (км/ч).

Ответ: 50 Пример 5. Велосипедист проехал 96 км на два часа быст- рее, чем предполагал. При этом за каждый час он проезжал на 1 км больше, чем ранее предполагал проезжать за 1 ч 15 мин. С какой скоростью (км/ч) он ехал ? Решение. Пусть велосипедист ехал со скоростью км/ч, а ранее предполагаемая скорость – км/ч. . Из условий задачи можно составить уравнения: откуда получаем, что (км/ч).

Ответ: .

Пример 6. Пловец плыл против течения реки. У первого моста он потерял пустую флягу. Проплыв ещё 20 минут против течения реки, он заметил свою потерю и вернулся, чтобы догнать флягу. Найти скорость (км/ч) течения реки, если пловец догнал флягу у второго моста, а расстояние между мостами равно 2 км. Решение. Пусть км/ч – скорость течения реки, км/ч – скорость пловца в стоячей воде. 20 мин. = ч.

73

км – расстояние, пройденное пловцом от первого моста до места обнаружения пропажи. ч – время, которое пловец плыл по течению. Из условия задачи можно составить уравнение: 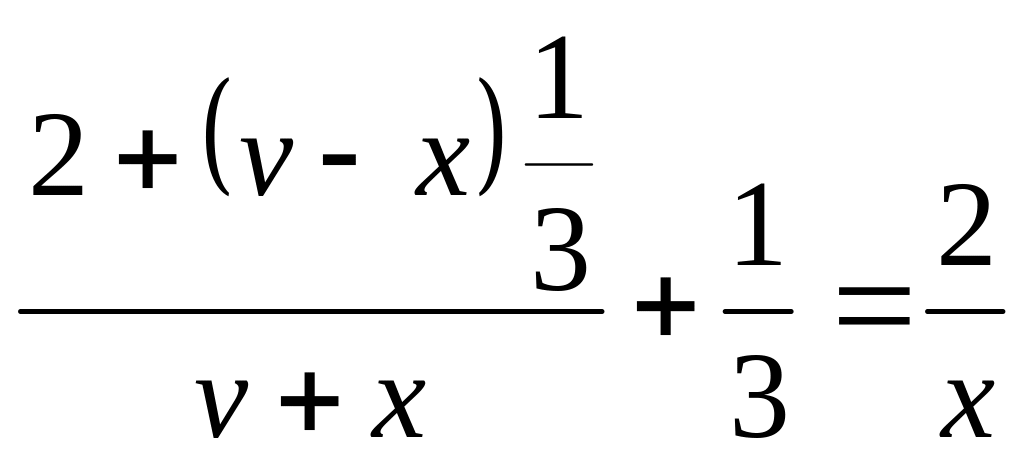, откуда ; (км/ч).

Ответ: 3. Задачи “на работу “ Пример 7. Токарь должен был изготовить 450 деталей за определенный срок. Перевыполняя ежедневно норму на 10 деталей, он изготовил 480 деталей за 3 дня до срока. Сколько деталей составляла ежедневная норма? Решение. Пусть ежедневная норма составляла деталей. Тогда – количество дней, необходимых для выполнения работы. В действительности токарь работал дней с производительностью деталей в день и изготовил 480 деталей. Следовательно, , откуда получаем: . Ответ: 30. Пример 8. Два каменщика сложили вместе стену за 20 часов. За сколько часов выполнил бы эту работу первый камен-

74

щик в отдельности, если ему пришлось бы работать на 9 часов больше второго? Решение. Объем работы примем за единицу; ч – время, за которое первый каменщик выполняет всю работу в отдельнос-ти, – производительность первого рабочего. Тогда ч – время, за которое второй каменщик выполняет всю работу в отдельности, – его производительность. Производительность совместной работы каменщиков равна сумме их производительностей. Следовательно, , откуда получаем: . Корни этого уравнения: . Значение не подходит по условию задачи. Поэтому, .

Ответ: 45. Задачи “на смеси” и “на сплавы” Пример 9. Сколько граммов воды нужно выпарить из 600 г 4 % - ого раствора поваренной соли, чтобы получить 5 % - ый раствор соли?

Решение. В 600 г 4 %-ого раствора соли содержится (г ) соли. Положим, что из раствора нужно выпарить г воды. Масса полученного 5 % -ого раствора рав- на г, а количество соли в этом растворе – . Следовательно, , т.е. , откуда .

Ответ: 120. Пример 10. Имеется лом стали двух сортов, причем первый сорт содержит 10 % никеля, а второй  30 %. На сколько тонн больше нужно взять лома стали второго сорта, чем первого, чтобы получить 200 тонн стали с содержанием никеля 25 % ?

75

Решение. Пусть надо взять тонн лома стали первого сорта и тонн лома стали второго сорта. Тогда

Отсюда: , .

.

Ответ: .

Пример 11. Имеются два слитка золота и серебра; в одном количество этих металлов находится в отношении 2 : 3, в другом – в отношении 3 : 7. Сколько килограммов каждого сплава нужно взять, чтобы получить 8 кг нового сплава, в котором золото и серебро были бы в отношении 5 : 11 ?

Решение. Положим, что надо взять кг первого сплава. Тогда в нём будет содержаться к г золота, а в кг второго сплава золота будет кг. По условию в 8 кг нового сплава должно содержаться золота кг. Следовательно, . Отсюда находим (кг). Ответ: 1 кг первого сплава, 7 кг второго сплава.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. На ковер повысили цену на 10 %, а затем еще на 15 %. На

сколько процентов больше стал стоить ковер после двух

повышений цены? (Ответ: 26,5) 2. При изготовлении в день по 324 детали план будет перевы-

полнен на 8 %. Сколько деталей нужно изготовить в день, чтобы перевыполнить план на 14 %? (Ответ: 342) 3. Магазином продано в первый день 50 % поступившего то-

76

вара, а во второй день – 25 % остатка. Сколько процентов

поступившего товара было продано за два дня? (Ответ: 62,5)

4. Свежие фрукты содержат 72% воды, а сухие  20%. Сколько

килограммов сухих фруктов получится из 40 кг свежих

фруктов? (Ответ: 14)

5. Аквариум частично заполнен водой. За месяц 40% воды ис-

парилось. При этом объем воздуха увеличился на 60%.

Сколько процентов объема аквариума занимала вода в конце

месяца ? (Ответ: 36)

6. Из двух сплавов, первый из которых имеет массу 12 кг и

содержит 70 % серебра, а второй 56 % серебра, получили

сплав, содержащий 60 % серебра. Найти массу второго

сплава (кг). (Ответ: 30) 7. Смешали 5 л сливок 35 %-ной жирности с 4 л сливок 20 %-ной жирности и к смеси добавили 1 л чистой воды.

Какова жирность (в %) полученной смеси? (Ответ: 25,5) 8. В сосуде находился 15% - ый раствор соли. Из сосуда отли-

ли содержимого, а оставшуюся часть долили водой так,

что сосуд оказался заполненным на первоначального объ-

ема. Найти процентное содержание соли в полученном

растворе. (Ответ: 8)

9. Два станка работали по 4 часа, причем за это время на пер-

вом станке было изготовлено на 16 деталей больше, чем на втором. Определить количество деталей, изготовленных на

первом станке, если известно, что на изготовление одной де-

тали первому станку требуется времени на 4 минуты мень-

ше, чем второму. (Ответ: 40) 10. Для перевозки 90 тонн груза было затребовано некоторое количество машин. В связи с тем, что на каждую машину

погрузили на 0,5 тонны меньше, чем предполагалось, до-

77

полнительно было затребовано 6 машин. Сколько машин

было затребовано первоначально ? (Ответ: 30)

11. Бригада должна была по плану заготовить за несколько

дней 216 м³ древесины. Первые 3 дня бригада выполня-

ла ежедневно установленную планом норму, а затем каж-

дый день заготовляла по 8 м³ сверх плана, поэтому за день

до срока было заготовлено 232 м³ древесины. Сколько ку-

бических метров древесины в день бригада должна была

заготовлять по плану? (Ответ: 24) 12. Путешественник предполагал пройти 30 км с некоторой

скоростью. Но с этой скоростью он шел всего один час, а

затем снизил скорость на 1 км/ч. В результате он прибыл в

конечный пункт на 1 час 15 минут позже, чем планировал.

С какой скоростью (км/ч) путешественник собирался

пройти путь? (Ответ: 5) 13. Двое рабочих выполняют некоторую работу. После 45 мин

совместной работы первый рабочий был переведен на дру-

гую работу, и второй рабочий закончил оставшуюся часть

работы за 2 ч 15 мин. За сколько часов мог бы выполнить

всю работу второй рабочий в отдельности, если известно,

что ему на это понадобится на 1 час больше, чем первому ?

(Ответ: 4) 14. Катер, скорость которого в стоячей воде 15 км/ч, отпра-

вился от причала вниз по течению реки и, пройдя 36 км,

догнал плот, отправленный от того же причала за 10 часов

до отхода катера. Найти скорость (км/ч) течения реки.

(Ответ: 3) 15. Из города А в город В, расстояние между которыми 20 км, была отправлена грузовая машина. Через 8 минут

вслед за ней выехал автобус, который прибыл в город В

одновременно с машиной. Скорость автобуса на 5 км/ч

больше скорости грузовой машины. Найти скорость (км/ч) автобуса. (Ответ: 30)

78

16. Баржа была разгружена с помощью двух подъемных кра-

нов в течение 15 ч , причем первый кран приступил к рабо-

те на 7 ч позднее второго. Известно, что первый кран, ра-

ботая один, может разгрузить баржу на 5 ч скорее, чем

второй. За сколько часов может разгрузить баржу второй

кран, работая отдельно? (Ответ: 25)

17. Сосуд в 20 л наполнен спиртом. Из него выливают неко-

торое количество спирта в другой сосуд, равный ему, и, за-

полнив остальную часть второго сосуда водой, дополняют этой смесью первый сосуд. Затем из первого отливают

20/3 л во второй, после чего в обоих сосудах содержится

одинаковое количество спирта. Сколько литров спирта пер-

воначально перелили из первого сосуда во второй?

(Ответ: 10)

18. Два лыжника стартовали один за другим с интервалом в 2

минуты. Второй лыжник догнал первого на расстоянии 1 км от точки старта. Дойдя до поворота на отметке 5 км, второй лыжник повернул обратно и встретился с первым.

Эта встреча произошла через 20 минут после старта пер- вого лыжника. Найти скорость (км/ч) первого лыжника. (Ответ: 12)

19. Двое рабочих выполнили вместе некоторую работу за 12

часов. Если бы сначала первый сделал половину этой рабо-

ты, а затем другой остальную часть, то вся работа была бы

выполнена за 25 часов. За какое время мог выполнить эту

работу каждый рабочий в отдельности? В ответе указать

меньшее количество часов. (Ответ: 20) 20. Ученик прочел книгу в 480 страниц, ежедневно читая оди-

наковое количество страниц. Если бы он читал каждый день

на 16 страниц больше, то прочел бы книгу на 5 дней рань-

ше. Сколько дней ученик читал книгу? (Ответ: 15) 21. К бассейну объемом 1200 м³ подведены две трубы: подаю-

щая и отводящая. Если открыть одновременно обе трубы,

то бассейн заполнится за 60 часов. Если же открыта только

79

одна труба, то заполнение бассейна водой продолжается на

два часа меньше, чем его освобождение от воды. Сколько воды ( м³ ) в час пропускает отводящая труба?

(Ответ: 100) 22. Два насоса разной производительности, работая одновре-

менно, могут наполнить резервуар за 2 часа. В начальный

момент два таких одинаковых резервуара были заполнены наполовину. Первым насосом перекачали содержимое од-

ного из них в другой, после чего с помощью второго насоса

заполнили освободившийся резервуар. Вся работа заняла 6

часов. Во сколько раз производительность второго насоса

больше производительности первого? (Ответ: 2)

23. Школьник должен был выйти из дома в 7.00, сесть в ожи-

давшую его машину и доехать на ней до школы к опреде-

ленному моменту. Однако он вышел из дома в 6.30 и по-

бежал в обратном направлении. Машина в 7.00 отправи-

лась вслед за ним и, нагнав его, доставила в школу с опо-

зданием на 10 минут. Во сколько раз скорость машины

превышает скорость бегущего школьника? (Ответ: 7)

24. Человек, спускающийся по движущемуся эскалатору, на-

считал 42 ступени, а поднимаясь по движущемуся эскала-

тору – 30 ступеней. Скорость подъема человека относи-

тельно эскалатора в 2 раза меньше скорости спуска. Ско-

рость эскалатора при спуске и подъеме одна и та же.

Сколько ступеней насчитает человек, спускаясь по непо-

движному эскалатору? (Ответ: 70)

25. Пешеход идет по обочине дороги со скоростью 5 км/ч. Каж-

дые 27 минут его обгоняет рейсовый автобус, а каждые

1,8 км мимо него проезжает встречный автобус. Найдите

интервал движения автобусов (в минутах), если известно,

что он одинаков в обоих направлениях.

(Ответ: 24)

80