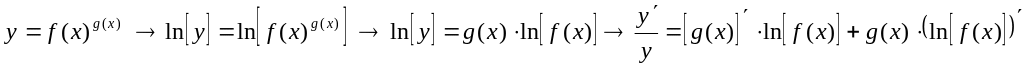Пределы. Производная
.doc
Эквивалентности при
|
Неопределенности |
Определенности |
|
|
|
II
замечательный предел
|
||
|
Формулы для разложения на множители и для избавления от корней:
![]()
![]()
![]()
![]()
Основные типы пределов:
Переменная |
Выражение |
Неопределенность |
Что делать |
|
|
|
Фиксируем старшую степень с коэффициентом |
|
|
|
Раскладываем на множители (если многочлен содержит корни, умножаем числитель и знаменатель на сопряженное выражение, чтобы получить ) |
|
|
|
Раскладываем на множители (если многочлен содержит корни, умножаем числитель и знаменатель на сопряженное выражение, чтобы получить ) |
|
|
|
Считаем по отдельности предел основания
и степени; попадаем в колонку
определенностей (2 нижние строки) или
во второй замечательный предел ( |
|
Выражения содержат
|
|
Используем эквивалентности. Помни: для множителей их можно применять всегда, а для слагаемых только в том случае, если их сумма (разность) не будет равна нулю (иначе сначала упрости выражение, а потом пользуйся эквивалентностями.) |
|
Выражения содержат |
|
Вводим подстановку
|
Производная (ПОМНИ - )
![]()
![]()
![]()
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная параметрически заданной функции:
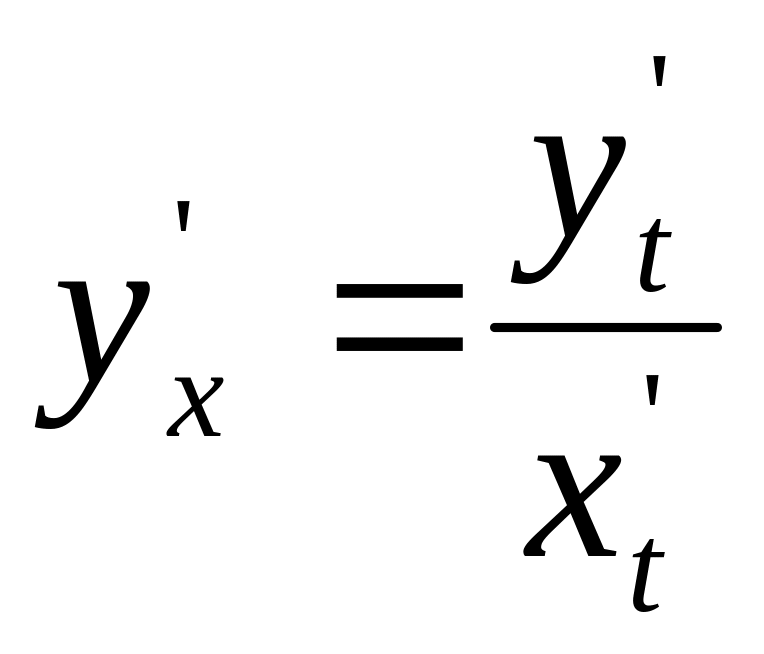
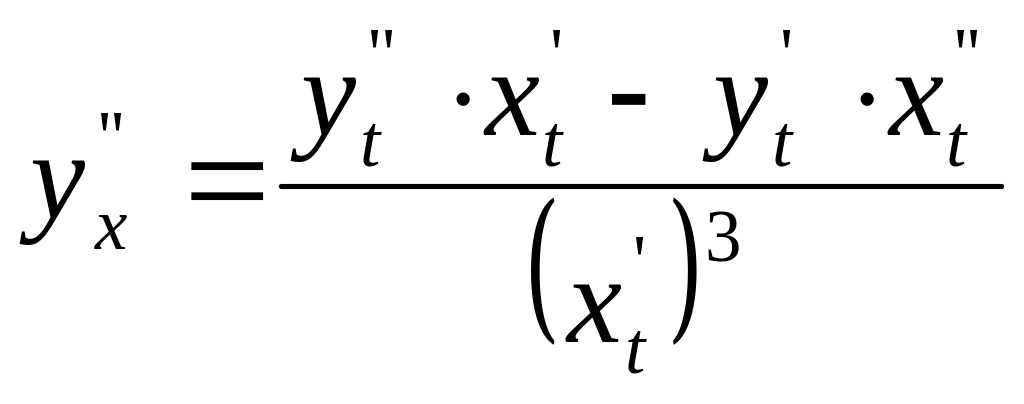
Производная неявно заданной функции:
![]()
![]()
Уравнение касательной: Уравнение нормали:
![]()
![]()
Дифференциал:
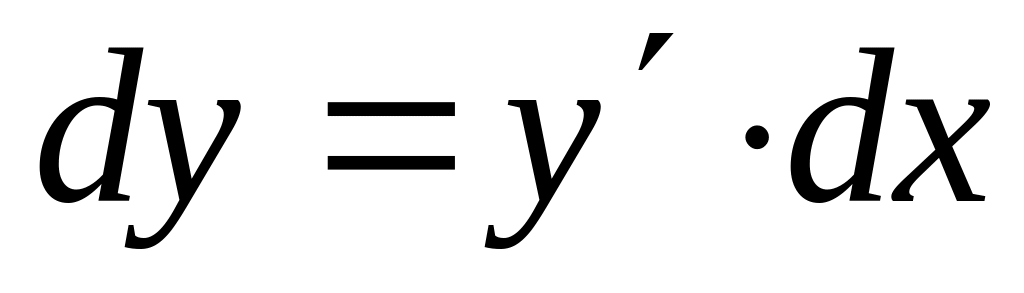
Приближенное вычисление с помощью дифференциала:
![]()
Помни, если видишь
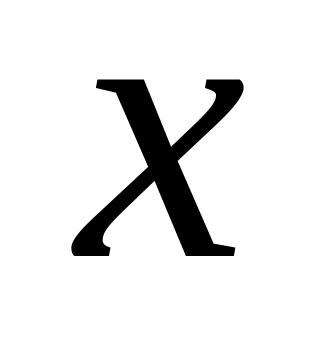 и в основании и в степени выражения, то
сначала прологарифмирую выражение, а
потом бери производную!!!!
и в основании и в степени выражения, то
сначала прологарифмирую выражение, а
потом бери производную!!!!