итоговый отчет
.pdfНа рисунке 8.2ж показана трещина, растущая по границе зерна бикристалла. Видеосъемка показывает, что она растет скачками и может внезапно, сменив направление роста,
перейти в объем зерна (рисунок 8.2з). Для деформируемого поликристалла характерно спонтанное образование за время ~ 1–3 с случайной сетки несоприкасающихся мезотрещин (размером порядка размера зерна), расположенных, в основном, по границам зерен, реже пересекающих отдельные зерна (Рисунок 8.2и); причем характерный масштаб
этой сетки, т.е. расстояния между наиболее удаленными мезотрещинами, может
достигать макроскопических размеров (~ 1 см), соизмеримых с размером образца.
Несмотря на большую суммарную площадь разрушения, образец макроскопически не разрушается. Обычно лавинообразное образование фрактальной сетки мезотрещин происходит незадолго до развития магистральной трещины в поликристаллическом льде.
Потенциал нестационарного электрического поля (сигнал ЭМЭ) измеряли с помощью плоского емкостного зонда размером 20 ×30 мм2, расположенного на расстоянии 5 мм от поверхности образца. Обнаружено, что процесс пластического деформирования, начиная с напряжения вблизи предела текучести до макроскопического разрушения образцов моно- и поликристаллического льда, сопровождается генерированием дискретных сигналов ЭМЭ и АЭ. На всех стадиях деформирования сигналы АЭ имели вид затухающих гармоник, форма которых, по данным калибровки,
совпадает с баллистической реакцией системы машина–образец. Поэтому идентификация динамических процессов структурной релаксации по форме сигналов АЭ представляет значительные трудности, которые ограничивают, как известно, применение метода АЭ в физических исследованиях. В тоже время форма сигналов ЭМЭ демонстрирует большое разнообразие (Рисунок 8.3). Синхронное видеофильмирование в поляризованном свете и измерение скачков пластической деформации высокочувствительным датчиком смещения позволяет, в принципе, производить идентификацию скачкообразных процессов пластической деформации и разрушения по сигналу ЭМЭ.
101
Рисунок 8.3 − Электромагнитная эмиссия при деформировании монокристаллического льда: 1 – кривая деформирования с постоянной скоростью роста напряжения σ0 = 5 кПа/с,
2 – сигнал ЭМЭ. На вставках представлены типичные сигналы ЭМЭ на различных стадиях деформирования.
102
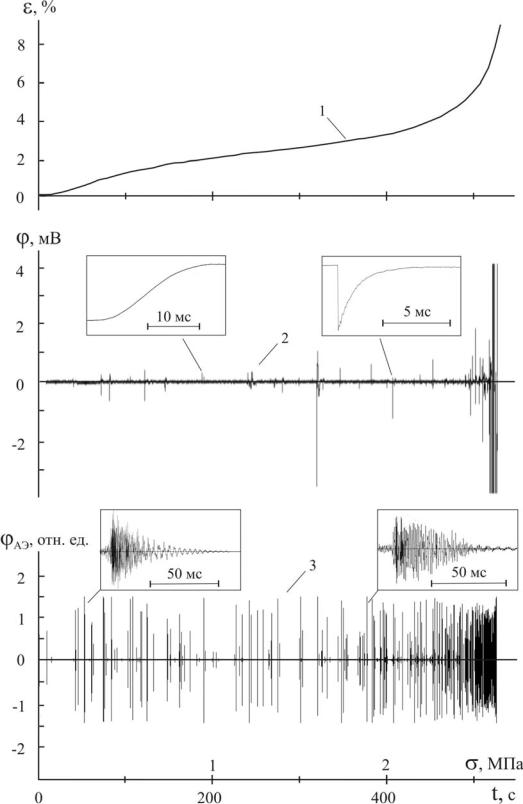
Рисунок 8.4 − Электромагнитная и акустическая эмиссия при деформировании льда: 1- кривая деформирования с постоянной скоростью роста напряжения σ0 = 5 кПа/с, 2 -
сигнал ЭМЭ; 3 - сигнал АЭ. На вставках представлены типичные сигналы ЭМЭ и АЭ на начальной и конечной стадии деформирования.
103
Несмотря на разнообразие форм сигналов ЭМЭ, их можно представить в виде последовательности импульсов почти треугольной формы, характеризуемых тремя основными параметрами: длительностью переднего фронта tfr, амплитудой ϕm и временем спада τd (Рисунок 8.5а), соизмеримого с максвелловским временем релаксации во льде
τM в области средних и низких частот. Наиболее информативной характеристикой сигнала оказалась величина tfr, которая определяется характерным временем поляризации кристалла, обусловленной эволюцией электрически активного структурно-кинетического элемента: дислокационного скопления и трещиной. По величине tfr импульсы ЭМЭ можно разделить на две группы: 1) импульсы I типа с tfr ~3×10-3 – 6×10-1 c, которые сопровождаются генерированием сигнала АЭ, но не сопровождаются появлением видимых микротрещин; 2) импульсы II типа с tfr ~ 10-5 – 3×10-4 с, вызванные по данным видеофильмирования зарождением и распространением трещин размером более ~100 мкм.
В серии экспериментов синхронно с видеофильмированием образца в поляризованном свете и регистрацией сигнала ЭМЭ записывали сигнал высокочувствительного датчика смещения штока машины. Обнаружено, что развитие одиночной полосы скольжения в монокристаллическом образце на начальной стадии
деформирования (ε ~ 0.5 −1% ) сопровождается |
скачком деформации |
h ~ 0.1−1 мкм и |
одновременно генерированием импульса ЭМЭ |
I типа (Рисунок 8.6а). |
В то же время |
развитие внутренних трещин длиной Lcr >100 мкм на стадии развитой деформации
( ε > 3% ) вызывает генерирование сигналов ЭМЭ II типа, но не вызывает заметного (в
пределах чувствительности метода) скачка деформации (Рисунок 8.6б).
Таким образом, две группы сигналов ЭМЭ – импульсы I и II типа – отражают два основных нестационарных (в полосе частот ~10–105 Гц) процесса в деформируемом кристалле: скачкообразную пластическую деформацию и разрушение. Вследствие существенного различия мгновенных скоростей пластического сдвига и распространения микротрещин, а, следовательно, характерных времен этих процессов, гистограмма передних фронтов t fr импульсов ЭМЭ имеет седлообразный вид (Рисунок 8.5б).
Существование интервала «запрещенных» значений t fr (седловая область гистограммы)
может быть использовано для более точного разделения сигналов на импульсы I и II типа,
что важно, например, для проведения статистического анализа скачков пластической деформации и/или разрушения.
104
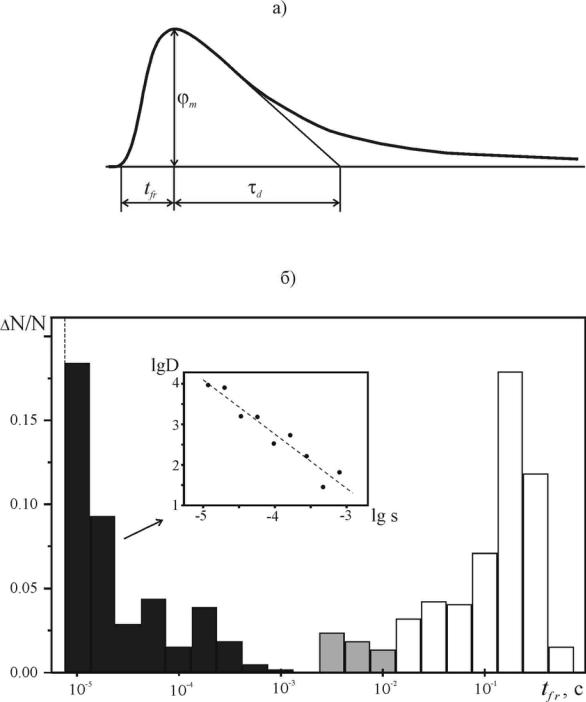
Рисунок 8.5 − а) Схематическое изображение импульса ЭМЭ: ϕm – амплитуда импульса, t fr – длительность переднего фронта, τd – время диэлектрической релаксации. б) Гистограмма передних фронтов t fr импульсов ЭМЭ. Черным цветом обозначены импульсы ЭМЭ II типа, связанные с развитием микро- и макротрещин, серым – импульсы ЭМЭ I типа, имеющие вид степенной функции ϕ( t ) ~ t1 / n , которые, обусловлены
динамикой консервативных скоплений дислокаций, а белым – импульсы ЭМЭ I типа с сигмовидной формой фронта, связанные с зарождением полос скольжения. На вставке представлена функция распределения D(s) для импульсов ЭМЭ II типа. Пунктирной линией отмечено временное разрешение метода (8 мкс), соответствующее максимальной тактовой частоте АЦП, равной 500 кГц.
105
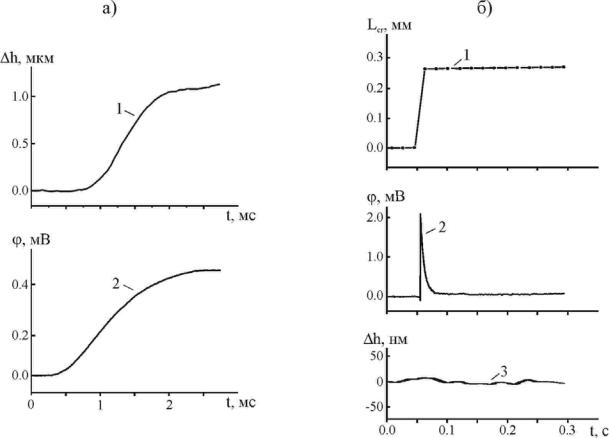
Рисунок 8.6 − Данные синхронной регистрации эволюции полосы скольжения и трещины оптическим и электромагнитным методами: а – синхронная запись скачка деформаций h
(1) и сигнала ЭМЭ I типа ϕ (2), вызванные развитием полосы скольжения (временной сдвиг между сигналом датчика смещения штока и сигналом ЭМЭ обусловлен инерционностью машины); б – синхронная видеозапись скачка длины трещины Lcr (1) вдоль оси сжатия, сигнала ЭМЭ II типа ϕ (2) и сигнала датчика смещения (3).
Из рисунка 8.5 видно, что гистограмма фронтов импульсов I типа, связанных со скачками
пластической деформации, имеет колоколообразный вид, в то время как гистограмма
фронтов импульсов ЭМЭ II типа, обусловленных зарождением и развитием в образце
микро- и макротрещин, описывается степенной статистикой: D(s) ~ s−r (см. вставку на
рисунок 8.5б), где D(s) = N −1δN(s)
δs – нормированная статистическая функция распределения величины s = t fr , δN(s) – число событий (импульсов ЭМЭ), попавших в
интервал от s до s +δs , а N – размер статистической выборки. Для всех исследованных
образцов моно- и поликристаллического льда показатель степени r находится в пределах
от 1.2 до 1.6. Таким образом, импульсы ЭМЭ I и II типа имеют не только различные
интервалы передних фронтов tfr, но и существенно различную статистическую функцию распределения этой величины.
106
Другой важной характеристикой сигнала является форма переднего фронта,
которая отражает кинетику соответствующих процессов структурной релаксации – скачков пластической деформации и разрушения. Среди одиночных импульсов ЭМЭ I
типа наблюдаются, по крайней мере, две основные формы: а) сигналы сигмовидной формы, близкой к логистической кривой роста популяции, наблюдаемые на всех стадиях пластической деформации, причем основная их доля приходится на интервал 0.5 < ε <2%;
б) сигналы, имеющие вид степенной функции ϕ( t ) ~ t1
n , где n = 2.1....2.5 , возникают на стадии развитой деформации, когда уровень приложенных напряжений достигает σ ~ 1
МПа в исследованных поликристаллических образцах и σ ≈ 3 − 4 МПа в
монокристаллическом льде; эти сигналы характеризуются самыми короткими фронтами t fr ≈ 3 −10 мс и вызваны, поэтому, наиболее быстрыми скачками пластической деформации (на гистограмме передних фронтов сигналов соответствующий интервал значений t fr отмечен серым тоном). Ниже на основе сравнения форм фронтов сигналов с моделями динамики скоплений дислокаций показано, что первые сигналы связаны с мезоскопическими процессами роста и обусловлены, в основном, зарождением и распространением полос скольжения, а вторые – с внезапным откреплением большого количества дислокаций: прорыв скопления через барьер и т.д.
107
9. ИССЛЕДОВАНИЕ ДИНАМИКИ И СТАТИСТИКИ ДИСЛОКАЦИОННЫХ ЛАВИН И ТРЕЩИН В ДЕФОРМИРУЕМОМ ЛЬДЕ НА СОНОВЕ ЭЛЕКТРОМАГНИТНОГО МОНИТОРИНГА
В предыдущей главе описан обнаруженный эффект генерирования электромагнитного сигнала при одноосном сжатии поликристаллического льда. Установлено, что сигнал электромагнитной эмиссии представляет суперпозицию «элементарных» сигналов – импульсов I и II типа, отображающих динамику различных процессов структурной релаксации – дислокационных скоплений и трещин. В настоящей главе описаны результаты исследования с помощью метода ЭМЭ статистики дислокационных лавин и трещин в деформируемом льде.
Подробный анализ динамического поведения консервативных скоплений дислокаций дан в работах [9, 14, 85, 92]. При свободном расширении скопления дислокаций, сконцентрированных в точке в момент времени t0 = 0, временная зависимость сдвига ε( t ) дается степенной функцией:
(9.1)
где m – показатель степени в законе υd ~ τ m для индивидуальных дислокаций. Из (9.1)
следует, что фазовая траектория такого скопления на плоскости « x − x » имеет вид гиперболы:
|
dx |
= Ax−m , |
|
(9.2) |
||
|
dt |
|
|
|
|
|
где x = ε , |
x = dx dt , A – |
|
постоянная, а |
на плоскости |
« lg x −lg x » |
– линейную |
зависимость: |
lg x = lg A −m lg x |
с наклоном, |
определяемым |
показателем |
степени m |
|
(Рисунок 9.1). В этом случае фазовый портрет свободно расширяющегося скопления непосредственно дает информацию о величине m , которая характеризует подвижность дислокаций в скоплении.
Анализ форм передних фронтов сигналов ЭМЭ I типа показал, что на стадии развитой деформации, когда уровень приложенных напряжений достигает σ ~1 МПа в исследованных поликристаллах и σ ~3÷4 МПа в монокристалле, возникают сигналы,
форма которых совпадает с зависимостью (9.1), т.е. ϕ( t ) ~ t1/( m+1 ) . Действительно, как следует из рисунок 9.1б, экспериментальные точки в координатах lg x – lg t
аппроксимируются линейными зависимостями с коэффициентом корреляции близким к
108
единице, что свидетельствует о хорошем согласии с моделью свободного расширения консервативного скопления дислокаций.
Из данных измерений сигнала ЭМЭ и оптических наблюдений можно оценить
средние |
скорости лидирующей |
группы |
дислокаций в консервативных скоплениях |
υ d ~ Lp |
t fr . Принимая максимальную длину скопления Lp, соизмеримой с размером зерна |
||
d~1-10 |
мм, получим υd ~ 1−5 |
м/с, что |
для большинства материалов соответствует |
области перегиба кривой υd (τ ) , наиболее трудной для моделирования подвижности дислокации. Данные о динамике дислокаций во льду в этой области скоростей в литературе отсутствуют. В условиях вязкого движения дислокаций (область «больших» скоростей; обычно υd >10 м/с), как известно, скорость дислокаций также пропорциональна
касательному напряжению (т. е. m = 1): υd = bτ
B , где В – коэффициент вязкого
торможения дислокаций, который в высокотемпературной области, точнее при температурах выше дебаевской, пропорционален температуре и определяется, в основном,
рассеянием фононов на упругом поле дислокации. Анализ форм сигналов ЭМЭ вида
ϕ( t ) ~ t1
( m+1 ) дает m = 1.3±0.2, поэтому можно предположить, что в областях
концентрации напряжений дислокации в скоплении движутся над рельефом Пайерлса, но
«вынуждены» термофлуктуационно преодолевать сетку локальных барьеров, связанных с
примесными центрами и молекулярными ионами OH − и Н3О+, которые не могут перемещаться с дислокацией (область предвязкого движения дислокаций).
В моделях эволюции дислокационного ансамбля обычно рассматриваются процессы зарождения дислокаций от неподвижных источников в объеме и на поверхности кристалла, размножение дислокаций механизмом ДПС, иммобилизации и аннигиляции дислокаций. С учетом этих процессов уравнение эволюции дислокационного ансамбля
записывают в виде:
|
ρ |
∂ρ |
=κ |
|
+ rρ + fρ3 2 −cρ2 + D 2 ρ , |
(9.3) |
||
|
|
0 |
||||||
|
|
∂ε |
d |
|
|
|
||
|
|
|
|
|
|
|
||
где k0 |
– коэффициент, зависящий от плотности неподвижных источников дислокаций, r |
|||||||
и c – |
коэффициенты размножения и иммобилизации дислокаций, f – |
коэффициент |
||||||
размножения на дислокациях леса, |
Dd |
– коэффициент диффузии дислокаций. |
||||||
Уравнение (9.3) |
анализируют обычно |
в контексте стадийности кривой |
нагружения. |
|||||
Начальные стадии деформирования |
льда |
характеризуются, как правило, низкой |
||||||
|
|
|
|
|
|
|
|
109 |
плотностью источников дислокаций. При зарождении и распространении скопления базисных дислокаций, которые не совершают двойное поперечное скольжение, можно пренебречь также и диффузионным членом в (9.3), а, следовательно, неоднородностью распределения дислокаций в скоплении. Тогда ρ играет роль полного числа дислокаций в скоплении Nd. Учитывая эти приближения, получим:
dx |
= rx −cx2 , |
(9.4) |
dt |
|
|
где x = Nd 
Ndm – безразмерная плотность подвижных дислокаций, Ndm – максимальное число дислокаций в ансамбле. Его решение
x(t) = (1+λe−rt )−1 |
(9.5) |
и фазовый портрет |
|
x = rx(1−λx) , |
(9.6) |
где λ = c r , представлены на рисунок 9.2. |
Уравнение (9.6) известно как логистическое |
уравнение Ферхюльста - Пирла [306, 307], которое описывает динамику численности изолированной однородной популяции с учетом внутривидовой конкуренции. На начальной стадии эволюции «популяции» подвижных дислокаций, когда основным
процессом является размножение дислокаций |
(«свободная популяция»), x(t) ~ ert , а при |
t → ∞ скорость роста асимптотически |
затухает как e−rt за счет роста роли |
иммобилизационных процессов, и численность «популяции» выходит на насыщение.
Сравнение функции (9.5) с типичным сигналом ЭМЭ сигмовидной формы показывает, что решение логистического уравнения лишь качественно отражает основные особенности формы сигнала: экспоненциальный рост на начальной стадии и асимптотический выход на насыщение (Рисунок 9.2а). Весьма приближенная аппроксимация обусловлена, по-видимому, сильным упрощением модели, в частности,
допущением, что кинетика скачка определяется только динамикой численности дислокаций, что эквивалентно предположению об их равных скоростях в ансамбле. Более корректное совпадение получено с нестационарными моделями роста в теории фазовых переходов первого рода.
Основными источниками дислокации на начальных стадиях деформирования кристаллов с ГЦК решеткой, в частности, льда Ih, являются источники Франка - Рида (Ф -
Р), в качестве которых выступают слабо закрепленные примесями сегменты сетки Франка из ростовых дислокаций [59]. Источник Ф - Р может произвести плоское скопление из
110