
- •Министерство образования и науки российской федерации
- •Рабочая программа учебной дисциплины бз.В.3 Геометрия
- •Распределение по семестрам
- •Пояснительная записка
- •Программа курса «Геометрия»
- •Содержание разделов
- •Раздел 1. Аналитическая геометрия. Преобразования плоскости.
- •Раздел 2. Методы изображений.
- •IV. Структура деятельности студента
- •VI. Рекомендуемая литература.
- •Контролирующие материалы
- •Вариант 7
- •Вариант 8
- •Вариант 10
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •II семестр
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •III семестр, ргз
II семестр
Контрольная работа №1
Вариант 1
Написать уравнение сферической поверхности, имеющей центр в точке С(4;5;-2), зная, что шар
 касается ее с внутренней стороны.
касается ее с внутренней стороны.Даны вершины треугольника А(4;1;-2), В(2;0;0), С(-2;3;-5). Через сторону АВ треугольника АВС провести плоскость, перпендикулярную к плоскости треугольника.
Найти расстояние между двумя параллельными прямыми:
 и
и .
.
Вариант 2
К сфере
 провести касательные плоскости,
параллельные плоскости
провести касательные плоскости,
параллельные плоскости .
.Через прямую
 провести плоскость, параллельную
плоскости
провести плоскость, параллельную
плоскости .
.Найти расстояние
 точки Р(1;3;5) от прямой
точки Р(1;3;5) от прямой .
.
Вариант 3
Составить уравнение сферы, если сфера имеет центр С(3;-5;-2) и плоскость
 является касательной к сфере.
является касательной к сфере.Написать уравнение плоскости, проходящей через прямую
 и параллельной прямой
и параллельной прямой .
.Вычислить расстояние
 точки Р(1;-1;-2) от прямой
точки Р(1;-1;-2) от прямой .
.
Вариант 4
Составить уравнение сферы, если она проходит через три точки М1(3;1;-3), М2(-2;4;1) и М3(-5;0;0), а ее центр лежит на плоскости
 .
.Через точку Р(1;0;7) параллельно плоскости
 провести прямую так, чтобы она пересекала
прямую
провести прямую так, чтобы она пересекала
прямую .
.Вычислить расстояние
 точки Р(2;3;-1) от прямой
точки Р(2;3;-1) от прямой .
.
Вариант 5
Составить уравнение сферы cцентром в точке Р(1;5;2), касающейся плоскости
 .
.Дана плоскость
 :
: и точка А(5;4;3). Найти точку В, симметричную
точке А относительно плоскости
и точка А(5;4;3). Найти точку В, симметричную
точке А относительно плоскости .
.Доказать, что прямые l1 иl2параллельны и найдите расстояние между ними, если
 и
и .
.
Вариант 6
Составить уравнение сферы с центром в точке Р(0;1;3) касающейся плоскости
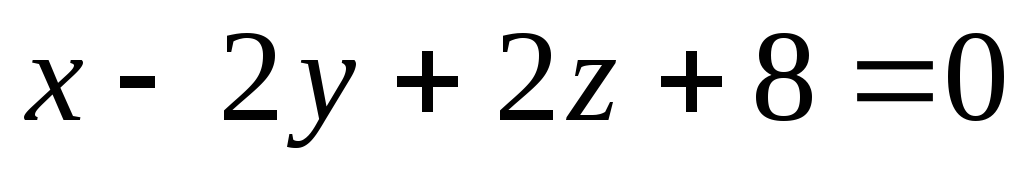 .
.Дана плоскость
 :
: и точка А(4;-7;-3). Найти точку В, симметричную
точке А относительно плоскости
и точка А(4;-7;-3). Найти точку В, симметричную
точке А относительно плоскости .
.Доказать, что прямые l1 иl2параллельны и найдите расстояние между ними, если
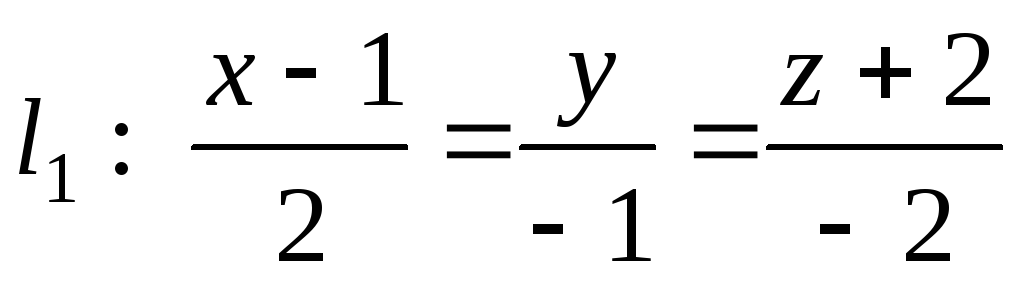 и
и .
.
Вариант 7
Составить уравнение сферы с центром в точке Р(3;0;1) касающейся плоскости
 .
.Дана плоскость
 :
: и точка А(4;8;-5). Найти точку В, симметричную
точке А относительно плоскости
и точка А(4;8;-5). Найти точку В, симметричную
точке А относительно плоскости .
.Доказать, что прямые l1 иl2параллельны и найдите расстояние между ними, если
 и
и .
.
Вариант 8
Составить уравнение сферы с центром в точке Р(-1;1;1) касающейся плоскости
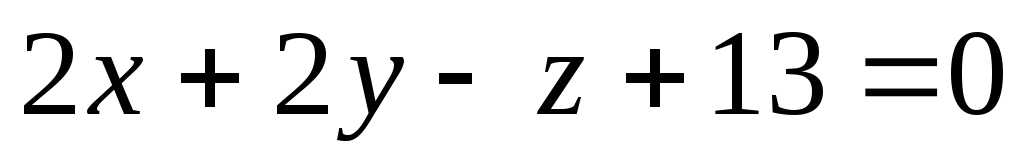 .
.Дана плоскость
 :
: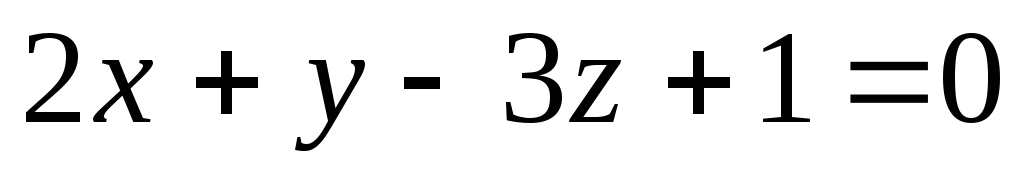 и точка А(-7;-3;4). Найти точку В, симметричную
точке А относительно плоскости
и точка А(-7;-3;4). Найти точку В, симметричную
точке А относительно плоскости .
.Доказать, что прямые l1 иl2параллельны и найдите расстояние между ними, если
 и
и .
.
Вариант 9
Составить уравнение сферы с центром в точке Р(0;0;2) касающейся плоскости
 .
.Дана плоскость
 :
: и точка А(3;-6;1). Найти точку В, симметричную
точке А относительно плоскости
и точка А(3;-6;1). Найти точку В, симметричную
точке А относительно плоскости .
.Доказать, что прямые l1 иl2параллельны и найдите расстояние между ними, если
 и
и .
.
Вариант 10
Составить уравнение сферы с центром в точке Р(1;0;1) касающейся плоскости
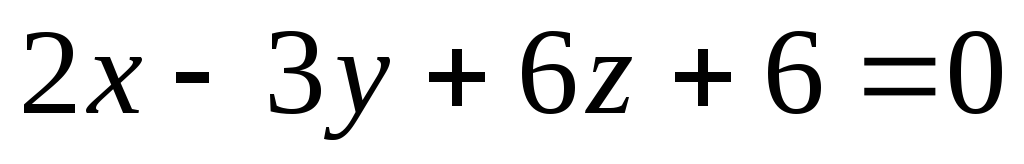 .
.Составить уравнение плоскости, проходящей через точку N(3;-1;2) параллельно прямой
 и перпендикулярной плоскости
и перпендикулярной плоскости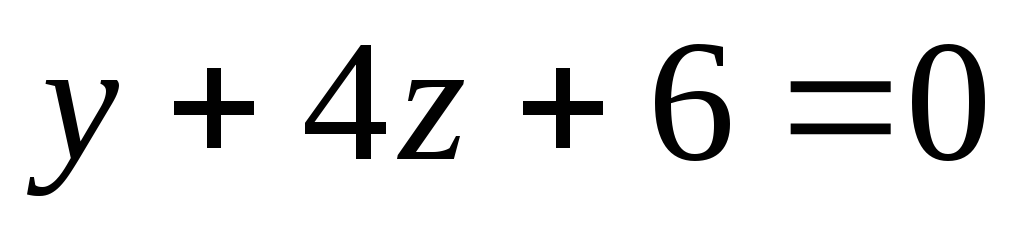
Доказать, что прямые l1 иl2параллельны и найдите расстояние между ними, если
 и
и .
.
Контрольная работа №2
Вариант 1
Найти центр поверхности:
 .
Какой вид примет это уравнение, если,
не меняя направления осей, перенести
начало координат в центр поверхности.
.
Какой вид примет это уравнение, если,
не меняя направления осей, перенести
начало координат в центр поверхности.Дан однополостный гиперболоид:
 и плоскость
и плоскость .
Определить направление хорд, которым
сопряжена диаметральная плоскость,
параллельная данной плоскости.
.
Определить направление хорд, которым
сопряжена диаметральная плоскость,
параллельная данной плоскости.Упростить уравнение поверхности:
 .
.
Вариант 2
Найти центр поверхности:
 .
Какой вид примет это уравнение, если,
не меняя направления осей, перенести
начало координат в центр поверхности.
.
Какой вид примет это уравнение, если,
не меняя направления осей, перенести
начало координат в центр поверхности.Найти диаметральную плоскость поверхности
 параллельную плоскости
параллельную плоскости и составить уравнение сопряженного ей
диаметра.
и составить уравнение сопряженного ей
диаметра.Упростить уравнение поверхности:
 .
.
Вариант 3
Пользуясь перенесением начала координат, упростить уравнение поверхности:
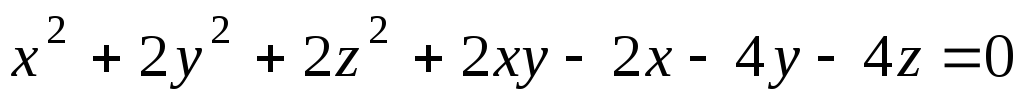 .
Найти центр поверхности.
.
Найти центр поверхности.Дан эллиптический параболоид:
 и две точки (3;0;5) и (0;4;7). Написать уравнение
диаметральной плоскости, проходящей
через данные точки, и определить
направление сопряженных ей хорд.
и две точки (3;0;5) и (0;4;7). Написать уравнение
диаметральной плоскости, проходящей
через данные точки, и определить
направление сопряженных ей хорд.Упростить уравнение поверхности:
 .
.
Вариант 4
Как преобразуется уравнение поверхности:
 ,
если перенести начало координат в центр
этой поверхности.
,
если перенести начало координат в центр
этой поверхности.Составить уравнение диаметральной плоскости поверхности
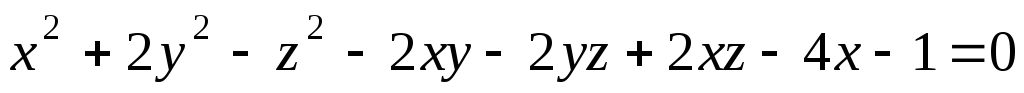 ,
проходящей через точки О(0;0;0) и М(1;1;0), и
найти вектор, параллельный сопряженным
ей хордам.
,
проходящей через точки О(0;0;0) и М(1;1;0), и
найти вектор, параллельный сопряженным
ей хордам.Упростить уравнение поверхности:
 .
.
Вариант 5
Преобразовать уравнение:
 ,
перенеся начало координат в центр этой
поверхности.
,
перенеся начало координат в центр этой
поверхности.Найти диаметральную плоскость поверхности
 ,
сопряженную с направлением вектора
,
сопряженную с направлением вектора .
.Упростить уравнение поверхности:
 .
.
Вариант 6
Преобразовать уравнение:
 ,
перенеся начало координат в центр этой
поверхности.
,
перенеся начало координат в центр этой
поверхности.Найти диаметральную плоскость поверхности
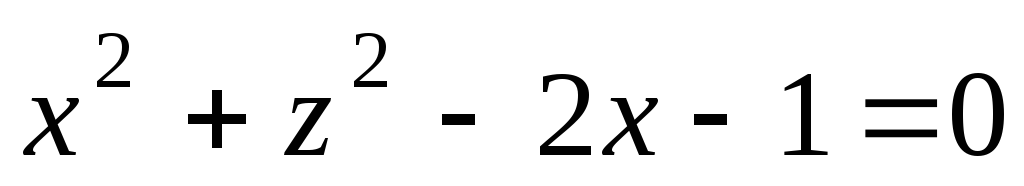 ,
проходящую через точку (2;1;0), а также
направление с ней сопряженное.
,
проходящую через точку (2;1;0), а также
направление с ней сопряженное.Упростить уравнение поверхности:
 .
.
Вариант 7
Преобразовать уравнение:
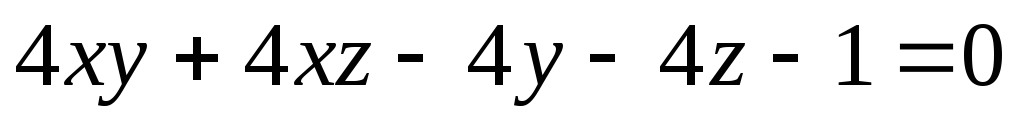 ,
перенеся начало координат в центр этой
поверхности.
,
перенеся начало координат в центр этой
поверхности.Найти диаметральную плоскость поверхности
 ,
проходящую через начало координат.
,
проходящую через начало координат.Упростить уравнение поверхности:
 .
.
Вариант 8
Преобразовать уравнение:
 ,
перенеся начало координат в центр этой
поверхности.
,
перенеся начало координат в центр этой
поверхности.Дана поверхность
 .
Найти диаметральную плоскость,
параллельную плоскости
.
Найти диаметральную плоскость,
параллельную плоскости .
.Упростить уравнение поверхности:
 .
.
Вариант 9
Преобразовать уравнение:
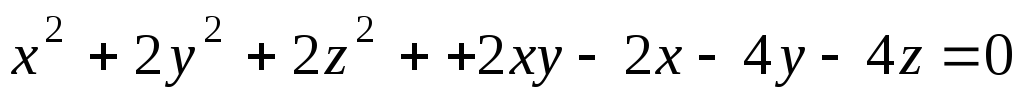 ,
перенеся начало координат в центр этой
поверхности.
,
перенеся начало координат в центр этой
поверхности.Найти диаметральную плоскость поверхности
 ,
сопряженную хордам, параллельным прямой
,
сопряженную хордам, параллельным прямой
Упростить уравнение поверхности:
 .
.
Вариант 10
Преобразовать уравнение:
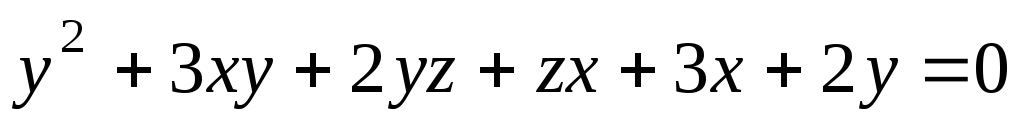 ,
перенеся начало координат в центр этой
поверхности.
,
перенеся начало координат в центр этой
поверхности.Найти главные направления поверхности
 .
.Упростить уравнение поверхности:
 .
.
Контрольная работа №3
Вариант 1
Даны три точки А(-1:2:1), B(3:0:1),C(5:-1:1). Убедитесь в их коллинеарности и найдите точкуDтакую, чтобы (ABCD)=2.
Найдите уравнение прямой, проходящей через точку A(3:-1:1) и полюс прямой
 относительно квадрики
относительно квадрики .
.
Методами проективной геометрии показать, что кривая
 является гиперболой и найти ее центр.
является гиперболой и найти ее центр.
Вариант 2
Даны три точки А(1:-1:2), B(-2:0:1),C(-1:-1:3). Убедитесь в их коллинеарности и найдите точкуDтакую, чтобы (CDBA)=-1.
Найдите полюс прямой
 относительно квадрики
относительно квадрики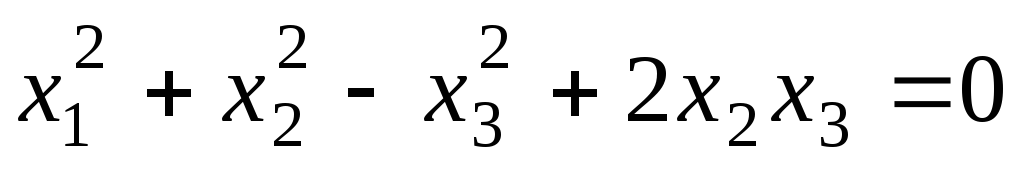 .
.
Методами проективной геометрии показать, что кривая
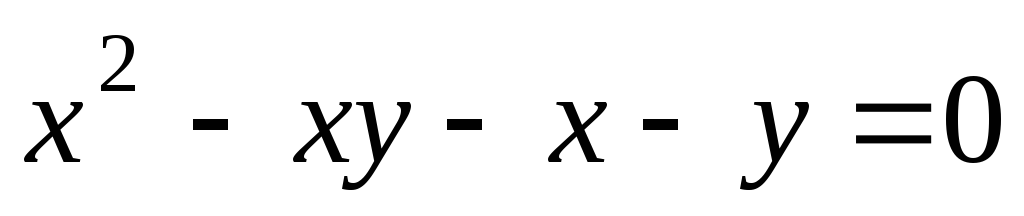 является гиперболой и найти ее асимптоты.
является гиперболой и найти ее асимптоты.
Вариант 3
Даны три прямые a(2:-1:1),b(1:3:1),c(5:1:-1). Убедитесь в их принадлежности одному пучку и найдите уравнение прямой
 из условия, что (abcd)=-1.
из условия, что (abcd)=-1.
Найдите уравнение поляры точки C(0:2:-1) относительно квадрики
 .
.Методами проективной геометрии показать, что кривая
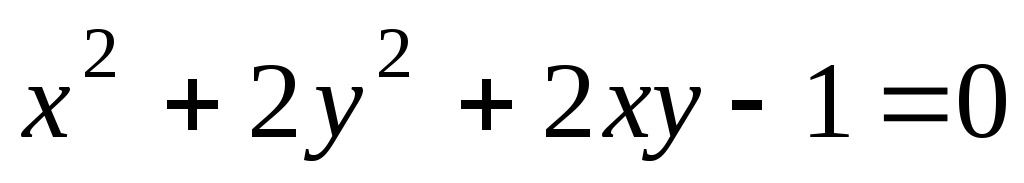 является
является
эллипсом и найти его центр.
Вариант 4
Даны прямые a(2:1:1),b(0:1:3),c(1:0:-1). Убедитесь в их принадлежности одному пучку и найдите в этом пучке прямую
 ,
такую, что (abcd)=
,
такую, что (abcd)=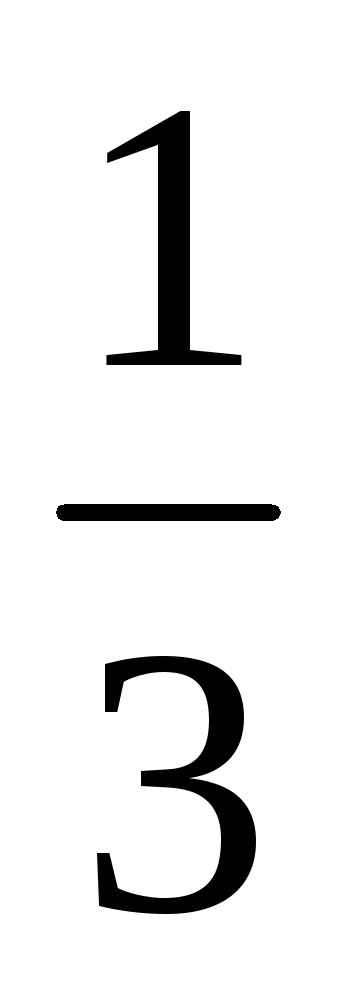 .
.
Найдите уравнение касательной к квадрике
 в ее точке А(1:1:0).
в ее точке А(1:1:0).
Методами проективной геометрии показать, что кривая
![]() является эллипсом и найти его центр.
является эллипсом и найти его центр.
Вариант 5
Даны три прямые a(2:-1:-1),b(1:3:1),c(5:1:-1). Убедитесь в их принадлежности одному пучку и найдите уравнение прямой
 из условия (abcd)=-1.
из условия (abcd)=-1.
Найдите уравнение касательной к квадрике
 в ее точке А(1:2:5).
в ее точке А(1:2:5).
Методами проективной геометрии показать, что кривая
![]() является эллипсом и найти его центр.
является эллипсом и найти его центр.
Вариант 6
Даны три точки А(-1:2:1), B(3:0:1),C(5:-1:1). Убедитесь в их коллинеарности и найдите точкуDтакую, чтобы (DBAC)=3.
Найдите уравнение касательной к квадрике
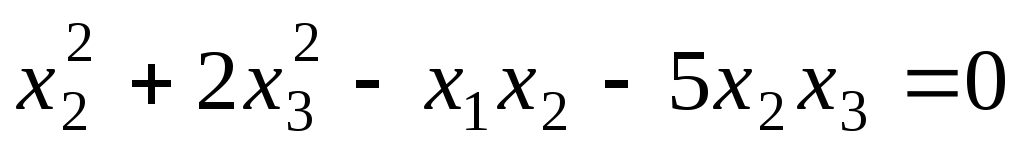 в ее точке
в ее точке
A(-1:1:2).
Методами проективной геометрии показать, что кривая
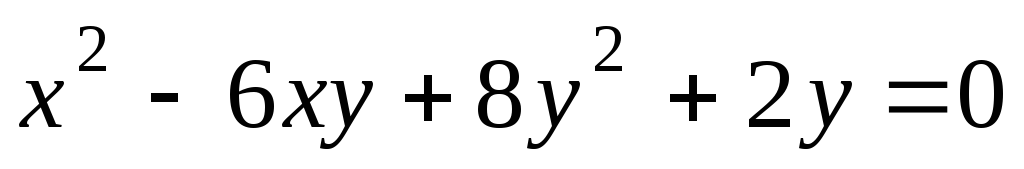
является гиперболой и найти ее центр.
Вариант 7
Даны три прямые a(2:-1:-1),b(1:3:1),c(5:1:-1). Убедитесь в их принадлежности одному пучку и найдите уравнение прямой
 из условия (abcd)=3.
из условия (abcd)=3.Найдите уравнение поляры точки A(1:2:1) относительно квадрики
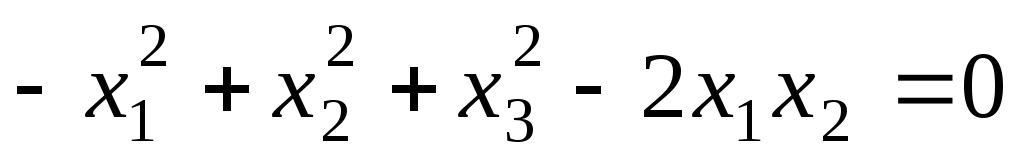 .
.Методами проективной геометрии показать, что кривая
![]() является гиперболой и найти ее центр.
является гиперболой и найти ее центр.
Вариант 8
Даны три точки А(-1:2:1), B(3:0:1),C(5:-1:1). Убедитесь в их коллинеарности и найдите точкуDтакую, чтобы (ADCB)=-5.
Найдите уравнение поляры точки A(-4:2:1) относительно квадрики
 .
.Методами проективной геометрии показать, что кривая
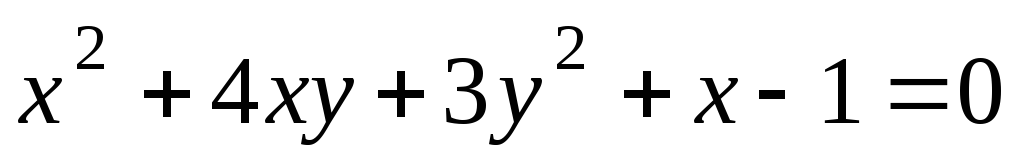
является гиперболой и найти ее центр.
Вариант 9
Даны три прямые a(2:-1:-1),b(1:3:1),c(5:1:-1). Убедитесь в их принадлежности одному пучку и найдите уравнение прямой
 из условия, что (dbac)=-2.
из условия, что (dbac)=-2.
Найдите полюс прямой:
 относительно квадрики
относительно квадрики .
.
3. Методами проективной геометрии
показать, что кривая
![]() является
является
эллипсом и найти его центр.
Вариант 10
Даны три точки А(-1:2:1), B(3:0:1),C(5:-1:1). Убедитесь в их коллинеарности и найдите точкуDтакую, чтобы (ABDC)=-1.
Найдите полюс прямой
 относительно квадрики
относительно квадрики .
.
Методами проективной геометрии показать, что кривая
 является гиперболой и найти ее асимптоты.
является гиперболой и найти ее асимптоты.
II семестр, РГЗ
Вариант 1
Написать уравнение прямой (АВ), если А(1:-2:0), В(-3:1:2) и записать ее координаты.
Найти координаты точки пересечения прямых
 и
и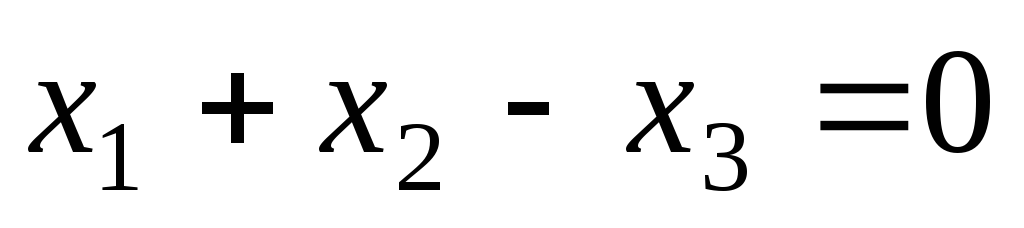 .
.Найти несобственную точку прямой
 .
.На евклидовой плоскости даны две параллельные прямые и на одной из них отрезок АВ. Пользуясь одной линейкой, удвойте отрезок АВ.
Найти (АВСД), если А(-2), В(1), С(3), Д(-4).
Даны точки А(1:0:1), В(1:-1:2), С(5:-2:7), Д(1:1:0). Докажите, что эти точки коллинеарны и найдите (АВСД).
Методами проективной геометрии показать, что кривая
 является эллипсом и найти его центр.
является эллипсом и найти его центр.Найти точки пересечения линии второго порядка
 с прямой (АВ), где А(5:0:-2) и В(1:3:-1).
с прямой (АВ), где А(5:0:-2) и В(1:3:-1).Найдите уравнение прямой, проходящей через точку (3:-1:1) и полюс прямой
 относительно
квадрики
относительно
квадрики .
.Задайте формулами проективное преобразование проективной прямой, переводящее точки А(1:2), В(1:1), С(1:-1) в точки А/(1:3), В/(3:4),C/(1:-2). Найдите неподвижные точки этого преобразования.
