19. Основы комплексного метода расчета цепи синусоидального тока.

 

Очень широкое распространение на практике получил символический, или комплексный, метод расчета цепей синусоидального тока.

Сущность символического метода расчета состоит в том, что при синусоидальном токе можно перейти от уравнений, составленных для мгновенных значений и являющихся дифференциальными уравнениями [см., например, (2.29)], к алгебраическим уравнениям, составленным относительно комплексов тока и ЭДС. Этот переход основан на том, что в уравнении, составленном по законам Кирхгофа для установившегося процесса, мгновенное значение тока i заменяют комплексной амплитудой тока  мгновенное значение напряжения на резисторе сопротивлением R, равное  — комплексом  по фазе совпадающим с током  мгновенное значение напряжения на индуктивной катушке  — комплексом опережающим ток на 90°; мгновенное значение напряжения на конденсаторе  Midt — комплексом  отстающим от тока на 90°; мгновенное значение ЭДС е — комплексом  Справедливость замены  на  следует из § 3.7 и 3.8.

В § 3.8 было показано, что амплитуда напряжения на L равна произведению амплитуды тока на  Множитель  свидетельствует о том, что вектор напряжения на индуктивной катушке опережает вектор тока на 90°.

Аналогично, из § 3.9 следует, что амплитуда напряжения на конденсаторе равна амплитуде тока, умноженной на  Отставание напряжения на конденсаторе от протекающего по ней тока на 90° объясняет наличие множителя 

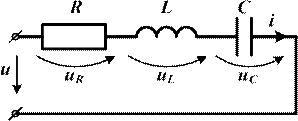
Например, для схемы рис. 3.9 уравнение для мгновенных значений можно записать так:

или

Запишем его в комплексной форме:

Вынесем  за скобку:

Следовательно, для схемы рис. 3.9

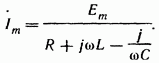
Это уравнение позволяет найти комплексную амплитуду тока  через комплексную амплитуду ЭДС  и сопротивления цепи 

Метод называют символическим потому, что токи и напряжения заменяют их комплексными изображениями или символами. Так,  — это изображение или символ падения напряжения  — изображение или символ падения напряжения  — изображение или символ падения напряжения на конденсаторе — 

20. Особенности расчета сложных цепей комплексным методом.

Существенное упрощение достигается изображением синусо­идальных функций времени комплексными числами.

Существует несколько форм представления комплексного числа:

- алгебраическая форма: ;

- показательная (или экспоненциальная) форма: ;

- тригонометрическая форма: .

Все эти формы связаны между собой, в частности, модуль числа , аргумент .

Для геометрического изображения используют прямоугольную систему координат, в которой по горизонтальной оси откладываются вещественные числа, а по вертикальной – мнимые: ; ; .

Для вещественной и мнимой частей комплексного числа употреб­ляют также обозначения: , .

Две комплексные величины, имеющие равные модули и равные, но противоположные по знаку аргументы, называют сопря­женными.

Если , то сопряженное ему комплексное число запишется в форме . При этом соблюдается равенство: .

Полезно помнить, что 

Пусть имеем синусоидально изменяющийся ток с начальной фазой φ_i .

Его можно представить в форме .

Таким образом, синусоидальный ток рассматривают как комплексное изображение синусоидального тока, которое при заданной частоте ω определяется двумяве­личинами – амплитудой и начальной фазой:

.

Здесь комплексное число называют комплексной амплитудой тока.

Рассмотрим теперь выражение для производной по времени от синусоидального тока:

.

Изображение производной будет иметь вид:

.

Таким образом, операция дифференцирования действительной функции заменяется умножением ее комплексного изображения на .

Рассмотрим изображение интеграла от сину­соидальной функции

.

Искомое изображение интеграла будет иметь вид:

.

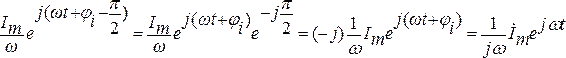Следовательно, операция интегрирования действительной функции заменяется делением ее комплексного изображения на .

Таким образом, комплексный метод позволяет заменить интегро-дифференциальное уравнение, содержащее функции времени, алгебраическим уравнением с их комплексными изображениями.

Алгоритм метода:

1. Замена заданных функций времени их комплексными изображениями.

2. Замена всех уравнений, составленных по закону Кирхгофа, алгебраическими уравнениями для комплексных изображений.

3. Нахождение комплексных изображений искомых функций.

4. Переход к оригиналам этих функций.

В качестве примера рассмотрим цепь с последовательно соединенными элементами R,L и C,к зажимам которой приложено напряжение, изменяющееся по синусоидальному закону . Требуется найти ток в цепи: .

1) Заменяем функции времени их изображениями: , .

2) Составляем уравнение по второму закону Кирхгофа:

.

Полученное уравнение является алгебраическим. Все слагаемые имеют общий множитель . Окончательно получаем уравнение в комплексных амплитудах:

.

3) Из последнего уравнения легко определяется комплексная ам­плитуда тока:

,

где – комплексное сопротивление цепи.

4) Зная выражение для комплексной амплитуды тока в виде , можем, используя обратный переход, записать выражение для мгновенного тока: .

Обычно рассматривают действующие значения токов и напряжений. Так как действующие синусоидальные токи и напряжения меньше их амплитуд в раз, то обычно вместо комплексных амплитуд рассмат­ривают комплексные действующие величины: , .

21. Топографическая диаграмма

Частным случаем векторной диаграммы является топографическая векторная диаграмма, на которой откладываются комплексные потенциалы отдельных точек цепи по отношению к одной точке, потенциал которой принят равным нулю. Порядок расположения векторов на топографической диаграмме соответствует порядку расположения элементов цепи.

Отметим, что по определению топографическая диаграмма используется как геометрическая интерпретация второго закона Кирхгофа (т.е. на ней откладываются векторы напряжений).

Существуют два способа построения топографической диаграммы.

I способ.

Строят, двигаясь по элементам цепи в направлении, совпадающем с направлением тока. В этом случае вектор напряжения на диаграмме и соответствующая стрелка напряжения на схеме ориентированы одинаково – от высшего потенциала к низшему.

Рассмотрим в качестве примера цепь рис. 3.15.

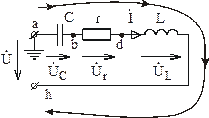
Рис. 3.15

Отложим на комплексной плоскости вектор тока  под углом  к действительной оси (рис. 3.16).

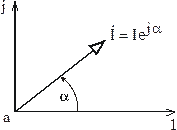
Рис. 3.16

Обозначим промежуточные точки рассматриваемой цепи буквами a, b, d, h. Обход контура будем совершать по направлению тока (т. е. по часовой стрелке), принимая комплексный потенциал точки а равным нулю. Последнее приводит к тому, что на комплексной плоскости точка а расположена в начале координат (рис. 3.16).

При движении в выбранном направлении по элементам цепи из точки а (рис. 3.15) первым элементом цепи является емкость с. Откладываем на топографической диаграмме из точки а вектор напряжения на емкости  , который отстает от тока на угол  (рис. 3.17). Конец вектора  определяет величину комплексного потенциала точки b на векторной диаграмме.

Следующий элемент цепи при движении по направлению тока – сопротивление r (см. рис. 3.15). Откладываем на топографической диаграмме вектор напря­жения на сопротивлении  , который совпадает по направлению с вектором тока  (рис. 3.18).

Рис. 3.17

Рис. 3.18

Конец вектора  определяет величину комплексного потенциала точки d на векторной диаграмме.

Следующий элемент цепи при движении по направлению тока – индуктивность L (см. рис. 3.15). Откладываем на топографической диаграмме вектор напряжения на индуктивности  , который опережает вектор тока  (рис. 3.19). Конец вектора  определяет величину комплексного потенциала точки h на векторной диаграмме.

Разность потенциалов точек a и h равна входному напряжению цепи  (см. рис. 3.15). Для получения соответствующего вектора на диаграмме необходимо соединить прямой линией точки a и h. Конец вектора  на диаграмме должен быть направлен так же, как и стрелка напряжения на схеме, – от точки а к точке h (рис. 3.20).

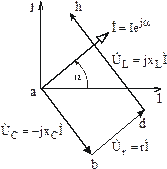
Рис. 3.19

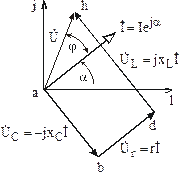
Рис. 3.20

Угол между векторами напряжения и тока (рис. 3.20) равен углу сдвига фаз  . В данном случае входное напряжение опережает ток и цепь имеет активно-индуктивный характер.

2 способ.

Строят, двигаясь по элементам цепи в направлении, противоположном направлению тока. В этом случае вектор напряжения на диаграмме направлен от точки низшего потенциала к точке высшего потенциала. Это же напряжение на схеме указывается стрелкой противоположного направления.

Итак, будем совершать обход цепи рис. 3.21 в направлении, противоположном току, принимая комплексный потенциал точки h равным нулю.

 

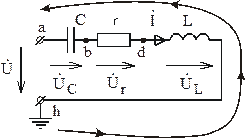
Рис. 3.21

Последнее приводит к тому, что на комплексной плоскости точка h расположена в начале координат (рис. 3.22).

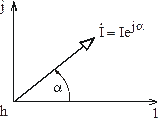
Рис. 3.22

При движении в выбранном направлении по элементам цепи из точки h (рис. 3.21) первым элементом цепи является индуктивность L. Откладываем на топографической диаграмме из точки h вектор напряжения на индуктивности  , который опережает вектор тока  (рис. 3.23). Конец вектора  определяет величину комплексного потенциала точки d на векторной диаграмме.

Рис. 3.23

Продолжая движение в выбранном направлении по элементам цепи и осуществляя аналогичные построения, получим результирующую топографическую диаграмму рис. 3.24.

Рис. 3.24

Сравнение векторных диаграмм рис. 3.20 и 3.24, построенных двумя способами, показывает их полную идентичность (векторы одноименных величин на диаграммах имеют одинаковое направление). Область преимущественного использования второго способа – трехфазные цепи.
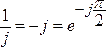