
mmt-11
.pdf
Пусть складываются колебания во взаимно перпендикулярных плоскостях и при этом их частоты не равны друг другу, а относятся друг к другу как целые
числа:
n
m
где n и m целые.
При этом отношение периодов равно обратной величине
T1 = m
T2 n
В этом случае на плоскости xy возникает фигура, называемая фигурой Лиссажу. Эта фигура вписана в прямоугольник со сторонами 2a, 2b.
Гармонические
колебания
Энергия
гармонических
колебаний
Векторная
диаграмма
Сложение
гармонических колебаний одного направления и одинаковой частоты
Биения
Сложение взаимно перпендикулярных колебаний
Фигуры Лиссажу
28/31
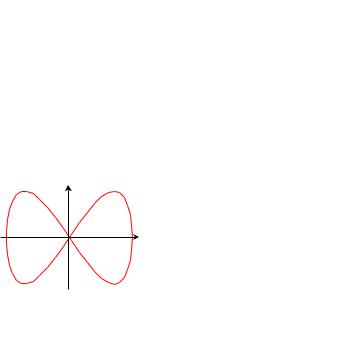
Чтобы по виду фигуры понять, как соотносятся периоды колебаний, нужно двигаясь вдоль линии фигуры пройти полный цикл по одной из координат и подсчитать, сколько циклов сделано при этом по другой координате.
x = a cos(ωt) |
y = b cos(2ωt + π/2) |
y |
x |
Гармонические
колебания
Энергия
гармонических
колебаний
Векторная
диаграмма
Сложение
гармонических колебаний одного направления и одинаковой частоты
Биения
Сложение взаимно перпендикулярных колебаний
Фигуры Лиссажу
29/31

x = a cos(2ωt) y = b cos(ωt)
y |
x |
Гармонические
колебания
Энергия
гармонических
колебаний
Векторная
диаграмма
Сложение
гармонических колебаний одного направления и одинаковой частоты
Биения
Сложение взаимно перпендикулярных колебаний
Фигуры Лиссажу
30/31
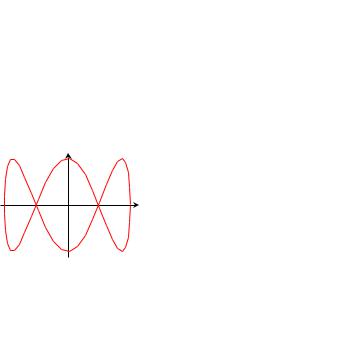
x = a cos(ωt)
y = b cos(3ωt − π/2)
y |
x |
Гармонические
колебания
Энергия
гармонических
колебаний
Векторная
диаграмма
Сложение
гармонических колебаний одного направления и одинаковой частоты
Биения
Сложение взаимно перпендикулярных колебаний
Фигуры Лиссажу
31/31
