Решением является точка a. Линейное программирование.

Задача линейного программирования состоит в оптимизации линейной функции на многогранном множестве , то есть математически она записывается следующим образом:

, (0)

, (0)

где

- вектор размерности ,,

- матрица размера ранга,

b - вектор размерности ,.

Скалярное произведение называетсяцелевой функцией. Коэффициенты целевой функции - это координаты вектора .

Множество называетсямножеством ограничений или допустимой областью задачи линейного программирования.

Задача (0) -называется задачей линейного программирования в каноническом виде.

Оптимальное значение целевой функции задачи линейного программирования может быть как конечным, так и неограниченным.

Для решения задач линейного программирования применяют симплекс-метод и его модификации.

Симплексный метод.

Симплексный метод - некоторая систематическая процедура решения задачи линейного программирования, состоящая в движении от одной экстремальной точки допустимой области к другой, с лучшим (или по крайне мере не худшим) значением целевой функции. Процесс продолжается до тех пор, пока не будет найдена либо оптимальная экстремальная точка, либо экстремальное направление , для которого (в этом случае оптимальное значение целевой функции неограниченно).

Для использования симплекс метода необходимо, чтобы задача линейного программирования представлялась в каноническом виде.

Задача линейного программирования, где многогранное множество записано в другом виде:

можно представить в каноническом виде, то есть записать неравенство в виде равенства. Для этого необходимо ввести неотрицательную дополнительную переменную :

Аналогично переменные , на которые не наложено требование не отрицательности переменных, представляются в виде:

Эти и некоторые другие преобразования используются для приведения задачи к каноническому виду. Подробное изложение симплекс-метода можно найти в [].

Основные теоремы линейного программирования.

Теорема 1(теорема существования).

Для того чтобы задача линейного программирования имела решение, необходимо и достаточно, чтобы допустимые множества как прямой, так и двойственной задач были непустые.

Теорема 2(теорема двойственности).

Некоторый допустимый вектор тогда и только тогда является решением задачи линейного программирования, когда существует такой допустимый вектор двойственной задачи, что значения целевых функций обеих задач на этих векторах равны.

Теорема 3(теорема о дополняющей нежесткости).

Для того, чтобы допустимые векторы x*, y* являлись решениями двойственных задач, необходимо и достаточно, чтобы они удовлетворяли условиям дополняющей нежесткости, то есть:

Альтернативные варианты, возникающие при решении задач линейного программирования.

нет решений

Графический метод решения задач линейного программирования.

При n=2 задачи линейного программирования можно решать графически.

F = c₁x₁ + c₂x₂  max (min)

a₁₁x₁ + a₁₂x₂  b₁

.

.

a_m1x₁ + a_m2x₂  b_m

x₁  0; х₂  0

Для этого напомним понятие градиента и линии уровня функции, необходимые при графическом решении задачи.

Градиент целевой функции f, обозначаемый f

Для линейной функции градиент представляется в виде

Градиент f показывает направление наискорейшего возрастания функции. Антиградиент (-f) показывает направление наискорейшего убывания функции.

Линия уровня функции - это линия, где функция имеет одинаковые значения. Для линейной функции f линии уровня перпендикулярны градиенту f.

Пример: 1

F= 1x₁ + 2x₂ max

x₁ + x₂  5

x₁  0; х₂  0

C₂

x₂

A f

5

f=10

S

5 B x₁

C₁

f=0

Рис. 10.

В точке А функция будет иметь максимальное значение.

Пример: 2

F= 1x₁ + 1x₂ max

x₁ + x₂  5

x₁  0; х₂  0

C₂

x₂

5 A f

S B

5 x₁

C₁

Рис. 11.

Решение задачи отрезок АВ

Пример: 3

f(x)=x₁+x₂max

x₁ + x₂  5

S x₁ + x₂  6

x₁  0; х₂  0

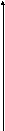
Рис. 12.

Решение нет, т.к. допустимая область S пуста.