Двойственные задачи линейного программирования.

В теории линейного программирования чрезвычайно важную роль играет то обстоятельство, что каждой задаче линейного программирования соответствует некоторая двойственная задача.

Если исходная задача (прямая)

при условии ,,

то двойственная задача представляет задачу на минимум

при условии ,,

то есть в развернутом виде:

прямая:

двойственная:

В экономике переменные двойственной задачи линейного программирования - это «теневые цены» лимитирующих ресурсов прямой задачи линейного программирования. «Теневая цена» ресурса показывает, насколько увеличится значение целевой функции при увеличении лимитирующего ресурса на единицу. Увеличение объема лимитирующего ресурса на единицу целесообразно только в том случае, если существует возможность его получения по стоимости, которая ниже, чем «теневая цена» данного ресурса.

Таблица для двойственных задач линейного программирования:

Если к двойственной задаче применить те же преобразования, какие были сделаны для прямой задачи, то вновь получаем исходную задачу линейного программирования (то есть двойственная к двойственной - есть исходная задача).

Устойчивость плановых решений (для модели однокритериального планирования)

Задача однокритериального планирования

f = c₁x₁ + c₂x₂  max (min)

a₁₁x₁ + a₁₂x₂  b₁

.

S .

a_m1x₁ + a_m2x₂ b_m

x₁  0; х₂  0

S – допустимая область решения

c_i – весовые коэффициенты целевой функции, ,

Сначала рассмотрим влияние интервалов неопределенности параметров c_i на устойчивость решения исходной задачи:

f = c₁x₁ + c₂x₂  max (min)

a₁₁x₁ + a₁₂x₂  b₁

.

S .

a_m1x₁ + a_m2x₂ b_m

x₁  0; х₂  0

При проверке на устойчивость мы должны перейти к следующим задачам:

f₁ = c₁ min x₁ + c₂ max x₂  max (2)

x  S

f₂ = c₁ max x₁ + c₂ min x₂  max (3)

x  S

Рис. 13.

Решением всех трех задач будет точка А. Решение устойчиво.

Правило: Если решение исходной задачи (1), не совпадает с решением задачи (2) или с решением задачи (3), то решение исходной задачи (1) при интервальной неопределенности неустойчиво, в противном случае решение исходной задачи (1) устойчиво.

Пример: Исходная задача (1)

f = c₁x₁ + c₂x₂  max

2х₁ + 3х₂  6

S:

x₁  0; х₂  0

с₁ = 1; с₂ = 2

с₁  [0,5 ; 1,5] с₂  [1,5 ; 2,5]

Проверить решение исходной задачи на устойчивость

Рис. 14.

Решение исходной задачи (1) не устойчиво, т.к. решения задач (1) и (3) не совпадают.

2 случай

f= c₁x₁+c₂x₂ → max

a₁₁x₁+a₁₂x₂ ≤ b₁

_.

_. (1)

_.

a_m1x₁+a_m2x₂≤ b_m

x₁≥0, x₂≥0

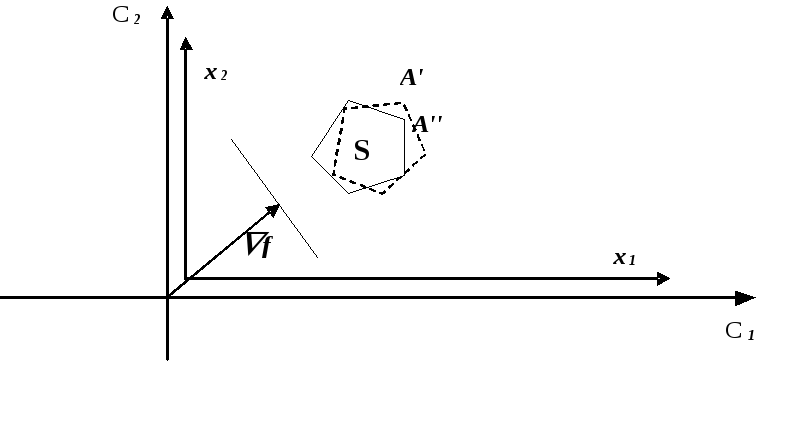
Рис. 15.

При такой интервальной неопределенности аji решение исходной задачи неустойчиво.

3 случай

f=c₁x₁ +c₂x₂ → max

a₁₁x₁+a₁₂≤b₁

_.

_.

a_m1x₁+a_m2x₂≤b_m

x₁≥0, x₂≥0

Рис. 16

Решение при такой интервальной неопределенности , решение задачи (1) неустойчиво.

Многокритериальный оптимальный план. Модель многокритериальной задачи линейного программирования.

.

.

a₁₁x₁ + a₁₂x₂  в₁

.

S .

a_m1x₁ + a_m2x₂ в_m

x₁  0; х₂  0

S – допустимая область решения

f_1…..f_l – частный критерий оптимальности

С^k_l – коэффициент частный критерий оптимальности

b_j – запасы j-ого вида ресурса, предназначено для выполнения критериального плана,

a_ji- расход j-ого ресурса на выпуск единиц i-ого вида продукта.