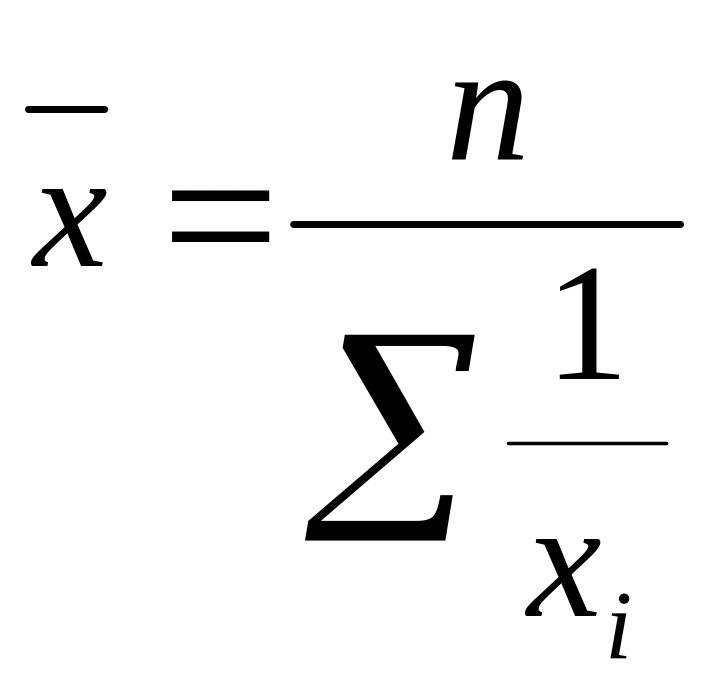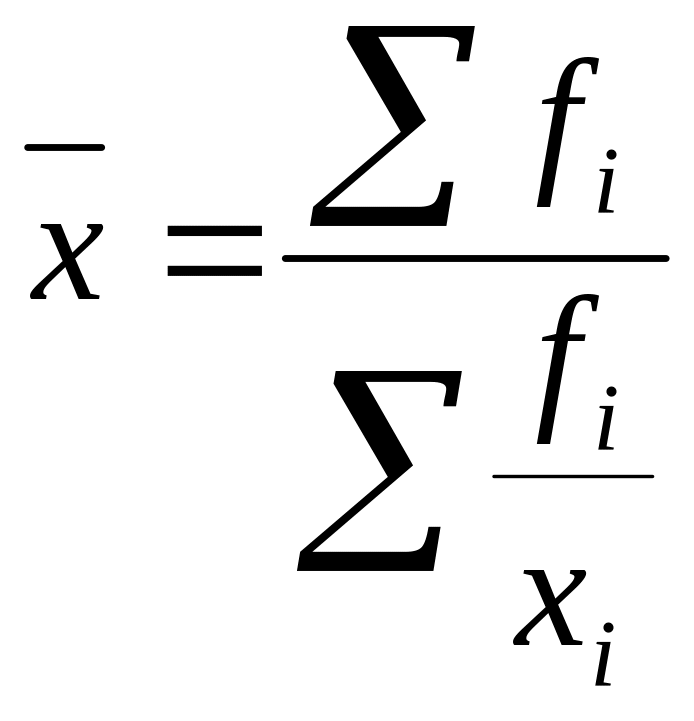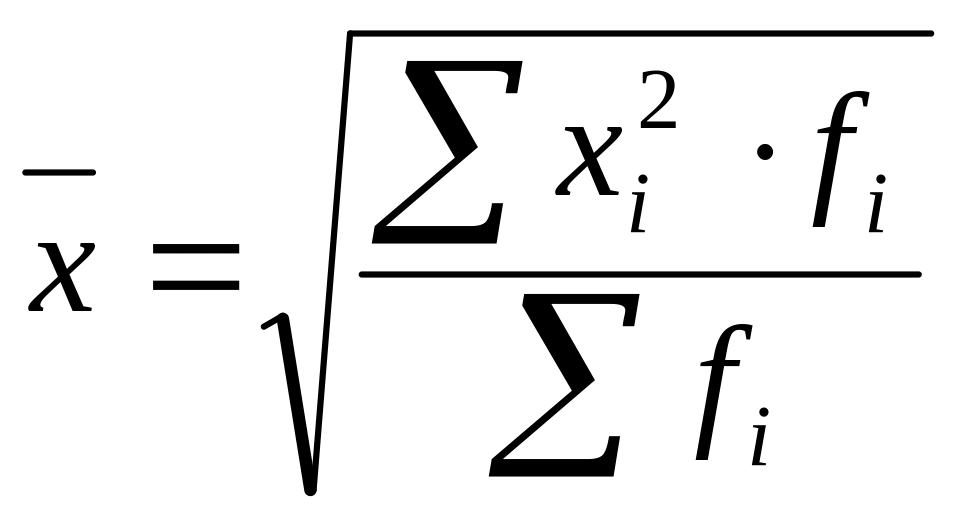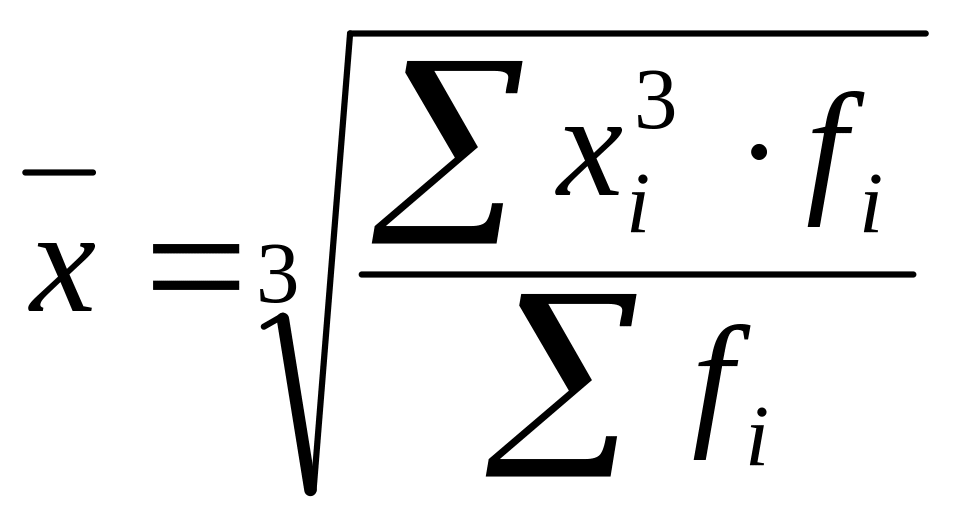3.1. Степенные средние величины.

Общая формула степенной средней записывается следующим образом:

.

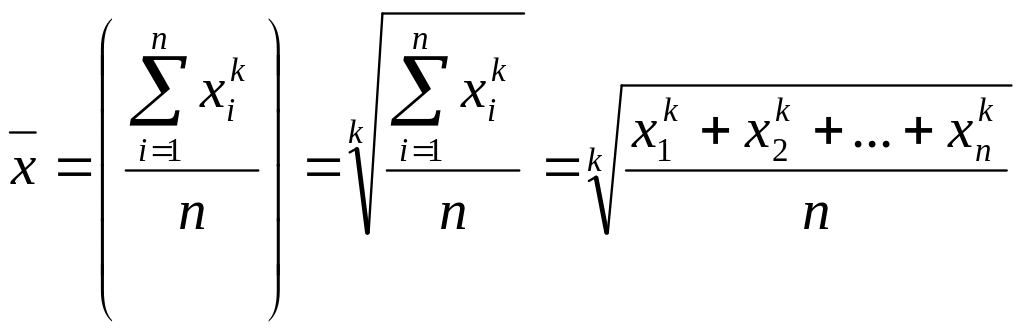С изменением показателя степени k выражение данной функции меняется, и в каждом отдельном случае приходим к определенному виду средней.

Запишем формулы различных видов степенных средних, придавая k значения: -1, 0, 1, 2.

При k = -1 получим среднюю гармоническую величину:

.

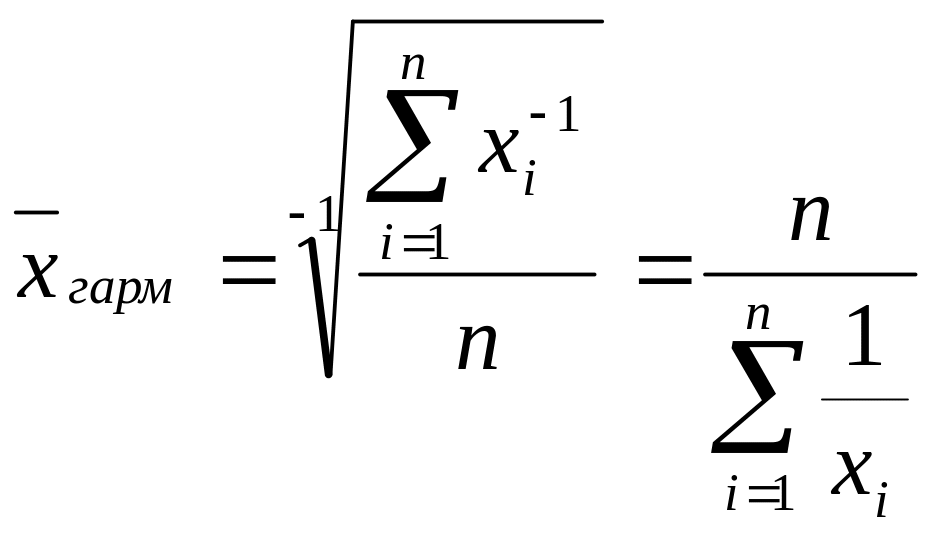При k = 0 получим среднюю геометрическую величину:

Для раскрытия неопределенности прологарифмируем обе части степенной средней:

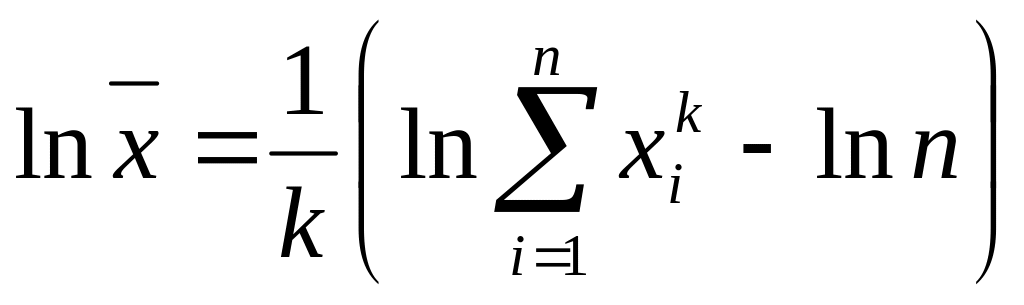
и, подставив k = 0, получим:

,

т.е. неопределенность типа 0/0.

Для ее раскрытия используем правило Лопиталя и найдем как предел отношения производных по k числителя и знаменателя в правой части равенства.

При k  0

Таким образом, при k = 0, , после потенцирования

При k = 1 получим среднюю арифметическую:

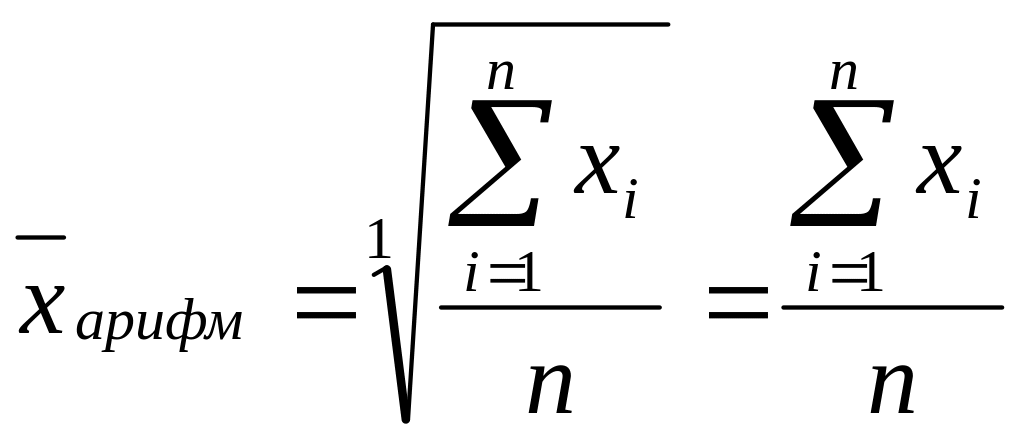
При k = 2 – среднюю квадратическую:

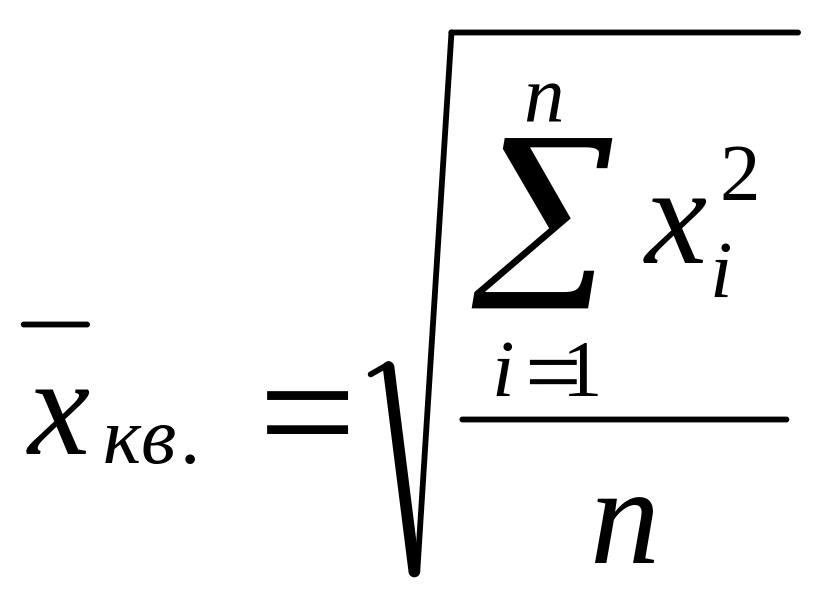
и т. д. для любой степени.

Приведенные выше формулы простых средних применяются в случае, если индивидуальные значения усредняемого признака не повторяются.

Если в практических исследованиях отдельные значения изучаемого признака встречаются несколько раз у единиц исследуемой совокупности, тогда частота повторения индивидуальных значений признака (вес) присутствует в расчетных формулах степенных средних. В этом случае они называются формулами взвешенных средних.

Формулы расчета различных видов степенных средних величин:

Наименова ние средней	Простая	Взвешенная
Средняя гармони- ческая
Средняя геометри- ческая
Средняя арифмети-ческая
Средняя квадрати- ческая
Средняя кубическая

где - частота повторения индивидуального значения признака (его вес).

Весом может быть и частость, т.е. отношение частоты повторения индивидуального значения признака к сумме частот:

.

Эти весовые коэффициенты образуют систему 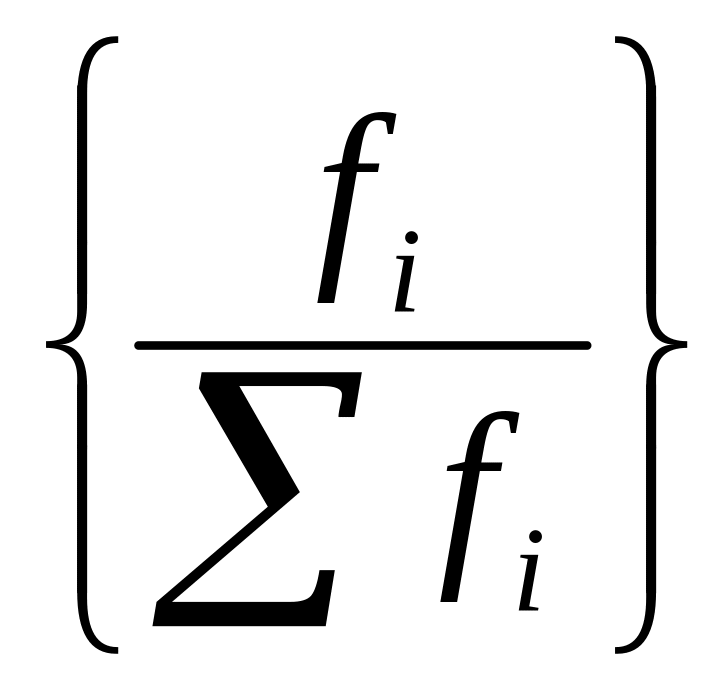. Сумма весовых коэффициентов равна 1.

Известно, что степенные средние разных видов, исчисленные по одной и той же совокупности, имеют различные количественные значения. И чем больше показатель степени k, тем больше и величина соответствующей средней:

_гарм. < _геом.< _арифм.< _кв.

Это свойство степенных средних возрастать с повышением показателя степени называется мажорантностью средних.

1. Средняя арифметическая. Является наиболее распространенным видом средних величин. В зависимости от исходных данных может быть простой или взвешенной.

Средняя арифметическая простая (невзвешенная) используется в тех случаях, когда расчет производится по несгруппированным данным. При ее вычислении общий объем признака мысленно распределяется между всеми единицами совокупности. Например, средняя заработная плата или средний доход работников предприятия – это такая сумма денег, которая приходилась бы на каждого работника, если бы весь фонд оплаты труда был распределен между всеми работниками поровну.

Пример. Требуется вычислить средний стаж работы 12 работников рекламного агентства. При этом известны индивидуальные значения признака (стажа) в годах:

6, 4, 5, 3, 3, 5, 5, 6, 3, 7, 4, 5.

Чтобы определить средний стаж работы, необходимо воспользоваться следующим исходным соотношением:

ИСС =	Совокупный стаж работы всех работников
	Количество работников

Формула для вычисления средней:

.

С учетом имеющихся данных получим:

года.

В этом случае мы использовали формулу средней арифметической простой (невзвешенной). Средняя арифметическая может оказаться дробным числом, если даже индивидуальные значения признака заданы только целыми числами. Это вытекает из сущности средней арифметической, которая есть величина абстрактная (теоретическая), т.е. она может принимать такое числовое значение, которое не встречается в представленной совокупности индивидуальных значений признака.

Под средней арифметической понимается такое значение признака, которое имела бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности.

В нашем примере одно и то же значение признака (стаж работы) встречается несколько раз. Объединив данные по величине признака и подсчитав число случаев повторения каждого из них, проведем расчет среднего стажа по сгруппированным данным с помощью формулы средней арифметической взвешенной:

Стаж работы, лет ( xi )	3	4	5	6	7	итого
Количество работников, Человек ( fi )	3	2	4	2	1	12

года.

При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам.

Пример. Распределение работников предприятия по возрасту:

Возраст (лет)	до 25	25-30	30-40	40-50	50-60	60 и более
Число работни ков (чел)	7	13	38	42	16	5

Для определения среднего возраста работника найдем середины возрастных интервалов. При этом величины открытых интервалов (первого и последнего) условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего). Середины интервалов будут следующими (x_i ):

22,5 27,5 35,0 45,0 55,0 65,0.

(чтобы определить середину интервала нужно к нижней границе прибавить правую и разделить на 2).

Средняя арифметическая взвешенная применяется также при вычислении общей средней для всей совокупности из частных (групповых) средних.

Пример. Рассчитать среднюю заработную плату в целом по трем предприятиям АО:

Предприятие	Численность промыш-ленно-производствен-ного персонала, чел.	Месячный фонд заработной платы, тыс. руб.	Средняя заработная плата, руб.
А	1	2	3
1	540	564,84	1046
2	275	332,75	1210
3	458	517,54	1130
Итого	1273	1415,13	?

Определим ИСС для показателя «средняя заработная плата». Независимо от имеющихся в нашем распоряжении данных средняя заработная плата может быть получена только через следующее отношение:

ИСС =	Фонд заработной платы
	Общая численность ППП

Предположим, что мы располагаем только данными о средней заработной плате и численности работников (гр.1 и 3), т.е. нам известен знаменатель исходного соотношения, но не известен его числитель. В этом случае фонд заработной платы можно получить умножением средней заработной платы ( x_i ) на численность ППП ( f_i ). Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:

руб.

Необходимо учитывать, что вес (f) в отдельных случаях может представлять собой произведение двух или даже трех значений.

2. Средняя гармоническая величина, как и средняя арифметическая, может быть простой и взвешенной.

Если веса у каждого значения признака равны, то можно использовать среднюю гармоническую простую. Однако в статистической практике чаще применяется средняя гармоническая взвешенная. Она используется, как правило, при расчете общей средней из средних групповых.

Предположим теперь, что в нашем распоряжении только данные о фонде заработной платы и средней заработной плате персонала (гр. 2 и 3), т.е. нам известен числитель исходного соотношения, но не известен его знаменатель. Численность работников по каждому предприятию можно получить делением фонда заработной платы на среднюю заработную плату. Тогда расчет средней заработной платы в целом по трем предприятиям будет произведен по формуле средней гармонической взвешенной:

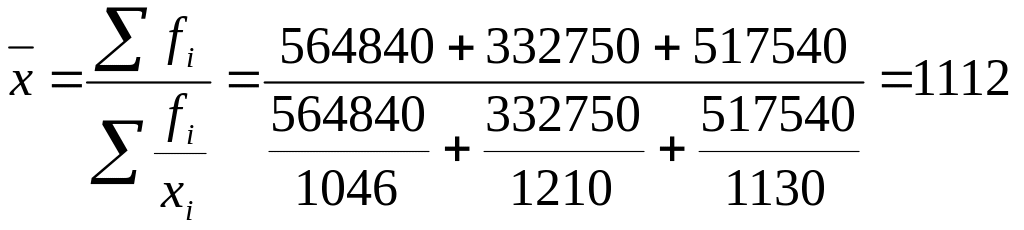руб.

В нашем примере мы использовали 2 разные формы средних, но получили один и тот же ответ. Это обусловлено тем, что для конкретных данных каждый раз реализовывалось одно и то же исходное соотношение средней.

3. Средняя геометрическая. При применении этого вида средней индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики. Используется в анализе динамики для определения темпов роста.

Средняя геометрическая величина используется также для определения равноудаленной величины от максимального и минимального значений признака. Например, если максимальный размер выигрыша в лотерее составляет миллион рублей, а минимальный – сто рублей, то какую величину выигрыша можно считать средней между миллионом и сотней? Арифметическая средняя явно непригодна, она составляет 500 050 руб., а это, как и миллион, крупный, а никак не средний выигрыш; он качественно однороден с максимальным и резко отличен от минимального. Не дают верного ответа ни средняя квадратическая (707 107 руб.), ни кубическая (793 699 руб.), ни средняя гармоническая (199, 98 руб.), слишком близкая к минимальному значению. Только геометрическая средняя дает верный с точки зрения экономики и логики ответ:

руб.

Десять тысяч – не миллион, и не сотня. Это действительно нечто среднее между ними.

4. Средняя квадратическая. Используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения. Так, при расчете показателей вариации среднюю вычисляют из квадратов отклонений индивидуальных значений признака от средней арифметической величины.

В статистической практике также находят применение степенные средние 3-го и более высоких порядков.